指数関数と対数関数の極限
本項では以下の内容を解説します。
- ・指数関数の極限
- ・対数関数の極限
- ・問題と解き方
【1】指数関数の極限
指数関数 \(\large{y=a^x}\) は、底\(\large{a}\) が 『\(\large{\boldsymbol{a>1}}\) の場合』 と 『\(\large{\boldsymbol{0 < a < 1}}\) の場合』でグラフの形状が変わります。
左図に 底\(\large{a}\) が \(\large{a>1}\) である場合、右図に 底\(\large{a}\) が \(\large{0 < a < 1}\) である場合の指数関数のグラフを示します。

(指数関数のグラフについては別の記事に解説しています)
左図から、指数関数は 底\(\large{a}\) が \(\large{a>1}\) である場合
・単調増加( \(\large{x}\)が増加すると \(\large{y}\) の値は常に増加する )
・\(\large{x}\) が負の方向に大きくなると \(\large{x}\)軸を漸近線として \(\large{y=0}\) に近づく
ことが分かります。
また、右図から、指数関数は 底\(\large{a}\) が \(\large{0< a < 1}\) である場合
・単調減少( \(\large{x}\)が増加すると \(\large{y}\) の値は常に減少する )
・\(\large{x}\) が正の方向に大きくなると \(\large{x}\)軸を漸近線として \(\large{y=0}\) に近づく
ことが分かります。
このような指数関数の性質から、極限は以下のようになります。
\(\displaystyle\large{\lim_{x \to \infty}a^x = \infty\hspace{1pt},\hspace{2pt} \lim_{x \to -\infty}a^x = 0}\)
・\(\large{0< a < 1 }\) のとき
\(\displaystyle\large{\lim_{x \to \infty}a^x = 0\hspace{1pt},\hspace{2pt} \lim_{x \to -\infty}a^x = \infty}\)
・例題
以下に指数関数の極限を利用した例題を解説します。
\(\displaystyle \large{(1)\hspace{5pt}\lim_{x \to \infty}2^x}\hspace{18pt}\)
\(\displaystyle \large{(2)\hspace{5pt}\lim_{x \to \infty}\left(\frac{1}{5}\right)^x}\)
例題1(1)は、指数関数の底が \(\large{2>1}\) であるため、 $$\large{\lim_{x \to \infty}2^x = \infty}$$ となります。
例題1(2)は、指数関数の底が \(\displaystyle \large{0 < \frac{1}{5} < 1}\) であるため、 $$\large{\lim_{x \to \infty}\left(\frac{1}{5}\right)^x = 0}$$ となります。
【2】対数関数の極限
対数関数 \(\large{y=\log_a x}\) は、底\(\large{a}\) が 『\(\large{\boldsymbol{a>1}}\) の場合』 と 『\(\large{\boldsymbol{0 < a < 1}}\) の場合』でグラフの形状が変化します。
左図に 底\(\large{a}\) が \(\large{a>1}\) である場合、右図に 底\(\large{a}\) が \(\large{0 < a < 1}\) である場合の対数関数のグラフを示します。
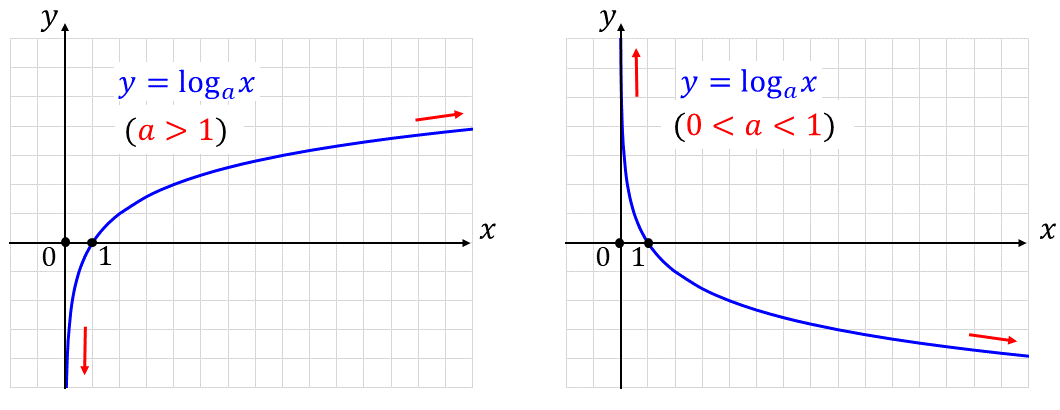
(対数関数のグラフについては別の記事に解説しています)
左図から、対数関数は 底\(\large{a}\) が \(\large{a>1}\) である場合
・単調増加( \(\large{x}\)が増加すると \(\large{y}\) の値は常に増加する )
・\(\large{x}\) が \(\large{0}\) に近づくと \(\large{y}\) 軸が漸近線となる
ことが分かります。
また、右図から、対数関数は 底\(\large{a}\) が \(\large{0< a < 1}\) である場合
・単調減少( \(\large{x}\)が増加すると \(\large{y}\) の値は常に減少する )
・\(\large{x}\) が \(\large{0}\) に近づくと \(\large{y}\) 軸が漸近線となる
ことが分かります。
このような対数関数の性質から、極限は以下のようになります。
\(\displaystyle\large{\lim_{x \to \infty}\log_a x = \infty\hspace{1pt},\hspace{2pt} \lim_{x \to +0}\log_a x = -\infty}\)
・\(\large{0< a < 1 }\) のとき
\(\displaystyle\large{\lim_{x \to \infty}\log_a x = -\infty\hspace{1pt},\hspace{2pt} \lim_{x \to +0}\log_a x = \infty}\)
・例題
以下に対数関数の極限を利用した例題を解説します。
\(\displaystyle \large{(1)\hspace{5pt}\lim_{x \to \infty}\log_3 x}\hspace{4pt}\)
\(\displaystyle \large{(2)\hspace{5pt}\lim_{x \to +0}\log_\frac{1}{2} x}\)
例題1(1)は、対数関数の底が \(\large{3>1}\) であるため、 $$\large{\lim_{x \to \infty}\log_3 x = \infty}$$ となります。
例題1(2)は、指数関数の底が \(\displaystyle \large{0 < \frac{1}{2} < 1}\) であるため、 $$\large{\lim_{x \to +0}\log_\frac{1}{2} x = \infty}$$ となります。
【3】問題と解き方
本章では、指数関数と対数関数の極限 に関連した問題について解説します。
\(\displaystyle \large{\lim_{x \to +0}3^{1/x}}\)
\(\displaystyle \large{\lim_{x \to \infty}\frac{2^x-5^x}{2^x + 5^x}}\)
\(\displaystyle \large{\lim_{x \to \infty}\frac{a^x-a^{-x}}{a^x}}\)
問題1, 2, 3 は 指数関数の極限の問題です。
(解答と解説 : 問題1 問題2 問題3)
\(\displaystyle \large{\lim_{x \to \infty}\log_3\frac{9x^2+5}{x^2+3}}\)
\(\displaystyle \large{\lim_{x \to \infty}(\log_2 (x+1)-\log_2(2x+1))}\)
\(\displaystyle \large{\lim_{x \to \infty}(\log_a (x^2-2)-\log_a x)}\)
問題4, 5, 6 は 対数関数の極限の問題です。
(解答と解説 : 問題4 問題5 問題6)
問題.1 指数関数の極限
\(\displaystyle \large{\lim_{x \to +0}3^{1/x}}\)
【解答と解説】
指数が \(\displaystyle\large{\frac{1}{x}}\) であるため、変数を置き換えて考えます。
\(\displaystyle\large{\frac{1}{x}=t}\) とおくと、\(\large{x \to +0}\) のとき \(\large{t \to \infty}\) であるから、 $$\large{\lim_{x \to +0}3^{1/x} = \lim_{t \to \infty}3^t}$$ 指数関数の底が \(\large{3>1}\) であることより 指数関数の極限から $$\large{\lim_{t \to \infty}3^t = \infty}$$ となります。
したがって、 $$\large{\lim_{x \to +0}3^{1/x} = \infty}$$ となります。
問題.2 指数関数の極限
\(\displaystyle \large{\lim_{x \to \infty}\frac{2^x-5^x}{2^x + 5^x}}\)
【解答と解説】
問題の式では極限を求めることができないため、分母と分子を \(\large{5^x}\) で割ることで式を変形します。
ここで、指数法則 \(\large{a^n\hspace{1pt} b^n = (a\hspace{1pt}b)^n}\) から $$\large{ 2^x \div 5^x = 2^x \times \left(\frac{1}{5}\right)^x =\left(\frac{2}{5}\right)^x}$$ となることから、以下のように変形されます。
$$\large{\lim_{x \to \infty}\frac{2^x-5^x}{2^x + 5^x} =\lim_{x \to \infty}\frac{\left(\frac{2}{5}\right)^x-1}{\left(\frac{2}{5}\right)^x + 1} }$$ ここで、底が \(\displaystyle\large{0 < \frac{2}{5} < 1}\) であることから、 $$\large{\lim_{x \to \infty}\frac{\left(\frac{2}{5}\right)^x-1}{\left(\frac{2}{5}\right)^x + 1} = -1}$$
したがって、 $$\large{\lim_{x \to \infty}\frac{2^x-5^x}{2^x + 5^x} = -1}$$
問題.3 指数関数の極限
\(\displaystyle \large{\lim_{x \to \infty}\frac{a^x-a^{-x}}{a^x}}\)
問題2 と同様に分母と分子を \(\large{a^x}\) で割ることで式を変形します。
\begin{eqnarray} \large \lim_{x \to \infty}\frac{a^x-a^{-x}}{a^x}&\large =&\large \lim_{x \to \infty}\frac{1-a^{-x}/a^x}{1} \\[0.5em] \large &\large =&\large \lim_{x \to \infty} (1-a^{-x}/a^x) \\ \end{eqnarray} ここで、指数法則 から $$\large{a^{-x} \div a^x = \left(\frac{1}{a}\right)^x \times \left(\frac{1}{a}\right)^x = \left(\frac{1}{a}\right)^{2x}}$$ したがって、 $$\large{\lim_{x \to \infty} (1-a^{-x}/a^x) = \lim_{x \to \infty} (1-(1/a)^{2x})}$$
ここで、底\(\displaystyle\large{\frac{1}{a}}\) の大きさにより場合分けをして解きます。
\(\displaystyle\large{\frac{1}{a}>1}\) すなわち \(\large{0 < a < 1}\) の場合
$$\large\lim_{x \to \infty} (1-(1/a)^{2x})= -\infty$$
\(\displaystyle\large{0 < \frac{1}{a} < 1}\) すなわち \(\large{a>1}\) の場合
$$\large\lim_{x \to \infty} (1-(1/a)^{2x}) = 1$$
となります。
したがって、
\(\large{0 < a < 1}\) のとき、\(\displaystyle\large{\lim_{x \to \infty}\frac{a^x-a^{-x}}{a^x} = -\infty}\)
\(\large{a > 1}\) のとき、\(\displaystyle\large{\lim_{x \to \infty}\frac{a^x-a^{-x}}{a^x} = 1}\)
問題.4 対数関数の極限
\(\displaystyle \large{\lim_{x \to \infty}\log_3\frac{9x^2+5}{x^2+3}}\)
そのまま極限を計算しようとすると 対数の真数が \(\large{\frac{\infty}{\infty}}\) の不定形となってしまいます。そのため、分母と分子を \(\large{x^2}\) で割ることで不定形を解消します。
\begin{eqnarray} \large \lim_{x \to \infty}\log_3\frac{9x^2+5}{x^2+3}&\large =&\large \lim_{x \to \infty}\log_3\frac{9+5/x^2}{1+3/x^2} \\[0.5em] \large &\large =&\large \log_3 9 \\[0.5em] \large &\large =&\large 2 \\ \end{eqnarray}
問題.5 対数関数の極限
\(\displaystyle \large{\lim_{x \to \infty}(\log_2 (x+1)-\log_2(2x+1))}\)
本問では、そのまま極限を計算しようとすると \(\large{\infty -\infty}\) の不定形となってしまいます。そのため、対数の公式から対数を変形して不定形を解消します。
\begin{eqnarray} &&\large\lim_{x \to \infty}(\log_2 (x+1)-\log_2 (2x+1)) \\[0.5em] \large &\large =&\large \lim_{x \to \infty}\log_2 \frac{x+1}{2x+1} \\[0.5em] &\large =&\large \lim_{x \to \infty}\log_2 \frac{1+1/x}{2+1/x} \\[0.5em] \large &\large =&\large \log_2 \frac{1}{2} \\[0.5em] \large &\large =&\large -1 \\ \end{eqnarray}
問題.6 対数関数の極限
\(\displaystyle \large{\lim_{x \to \infty}(\log_a (x^2-2)-\log_a x)}\)
まず、対数の公式から、式を変形すると、 \begin{eqnarray} &&\large \lim_{x \to \infty}(\log_a (x^2-2)-\log_a x)\\[0.5em] \large &\large =&\large \lim_{x \to \infty}\log_a \frac{x^2-2}{x} \\[0.5em] \large &\large =&\large \lim_{x \to \infty}\log_a (x-\frac{2}{x}) \\[0.5em] \end{eqnarray}
ここで、底\(\displaystyle\large{a}\) の大きさにより場合分けをして解きます。
\(\displaystyle\large{0 < a < 1}\) の場合
$$\large\lim_{x \to \infty}\log_a (x-\frac{2}{x}) = -\infty$$
となります。
\(\displaystyle\large{a>1}\) の場合
$$\large\lim_{x \to \infty}\log_a (x-\frac{2}{x}) = \infty$$
したがって、
\(\large{0 < a < 1}\) のとき
\(\displaystyle\large{\lim_{x \to \infty}(\log_a (x^2-2)-\log_a x) = -\infty}\)
\(\large{a > 1}\) のとき
\(\displaystyle\large{\lim_{x \to \infty}(\log_a (x^2-2)-\log_a x) = \infty}\)
となります。