対数関数のグラフ
本項では、『対数関数のグラフの特徴』 や 『グラフの書き方の問題』 について解説します。
【1】対数関数のグラフ
底を \(\large{a}\)、真数を \(\large{x}\) とした以下のような関数を対数関数といいます。 $$\large{y=\log_a x}$$
対数関数のグラフの形状は、底\(\large{a}\) の大きさが『\(\large{\boldsymbol{a > 1}}\) の場合』と『\(\large{\boldsymbol{ 0 < a < 1}}\) の場合』で分けられます。
【1-1】a>1 の場合の対数関数のグラフ
底が \(\large{a>1}\) であるような対数関数は、単調増加(\(\large{x}\) が大きくなると、常に \(\large{y}\) の値も大きくなる)の性質があります。
例えば、以下に \(\large{y=\log_2 x}\) のグラフを示します。

図中の赤い点は \(\large{y}\) の値が \(\large{-2}\) から \(\large{4}\) までの整数となるグラフ上の点をプロットしています。
| \(\large{x}\) | \(\displaystyle \large{\frac{1}{4}}\) | \(\displaystyle \large{\frac{1}{2}}\) | \(\large{1}\) | \(\large{2}\) | \(\large{4}\) | \(\large{8}\) | \(\large{16}\) |
|---|---|---|---|---|---|---|---|
| \(\large{y}\) | \(\large{-2}\) | \(\large{-1}\) | \(\large{0}\) | \(\large{1}\) | \(\large{2}\) | \(\large{3}\) | \(\large{4}\) |
上図から分かるように \(\large{a > 1}\) のときの \(\large{y=\log_a x}\) のグラフには、以下の特徴があります。
2. \(\large{a > 1}\) のとき単調増加(\(\large{x\hspace{2pt}}\)が増加すると\(\large{y\hspace{2pt}}\)も増加)
3. 点\(\large{(1,0)}\),点\(\large{(a,1)}\)を通る
4. \(\large{y}\)軸に漸近する
【1-2】0 < a < 1 の場合の対数関数のグラフ
底が \(\large{0 < a < 1}\) であるような対数関数は、単調減少 (\(\large{x}\) の値が大きくなれば、常に \(\large{y}\) の値が小さくなる) の性質があります。
例えば、以下に \(\large{y=\log_\frac{1}{2} x}\) のグラフを示します。

図中の赤い点は \(\large{y}\) の値が \(\large{-4}\) から \(\large{2}\) までの整数となるグラフ上の点をプロットしています。
| \(\large{x}\) | \(\displaystyle \large{\frac{1}{4}}\) | \(\displaystyle \large{\frac{1}{2}}\) | \(\large{1}\) | \(\large{2}\) | \(\large{4}\) | \(\large{8}\) | \(\large{16}\) |
|---|---|---|---|---|---|---|---|
| \(\large{y}\) | \(\large{2}\) | \(\large{1}\) | \(\large{0}\) | \(\large{-1}\) | \(\large{-2}\) | \(\large{-3}\) | \(\large{-4}\) |
上図から分かるように \(\large{0 < a < 1}\) のときの \(\large{y=\log_a x}\) のグラフには、以下の特徴があります。
2. \(\large{0 < a < 1}\) のとき単調減少(\(\large{x}\)が減少すると\(\large{y}\)も減少)
3. 点\(\large{(1,0)}\),点\(\large{(a,1)}\)を通る
4. \(\large{y}\)軸に漸近する
【1-3】対数関数と指数関数のグラフの関係
対数関数 \(\large{y = \log_a x}\) を指数で表記すると、\(\large{x = a^y}\) となります。
このとき、\(\large{x}\) と \(\large{y}\) を入れ替えると、指数関数 \(\large{y = a^x}\) と一致します。
ここで、\(\large{a=2}\) のときの対数関数 \(\large{\color{blue}{y = \log_2 x}}\) と 指数関数 \(\large{ \color{red}{y=2^x}}\) のグラフを示します。
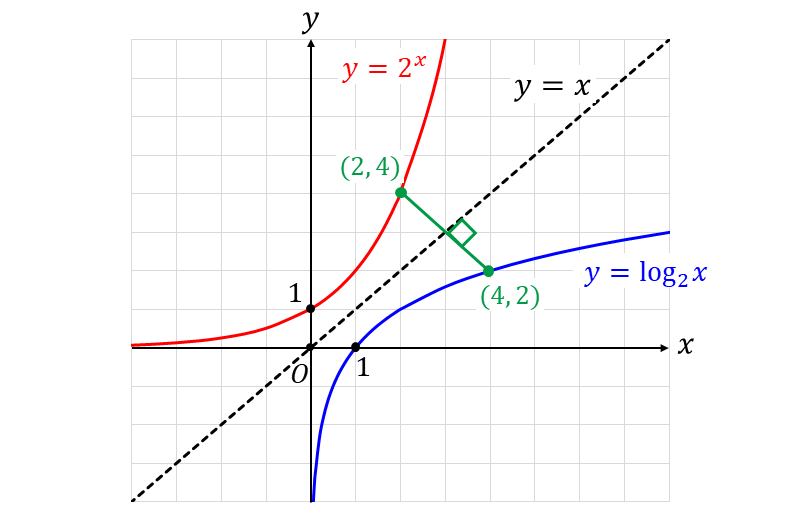
上図のように、対数関数 \(\large{y = \log_2 x}\) と 指数関数 \(\large{y = 2^x}\) は、\(\large{y=x}\) に関して対称移動したグラフとなっていることが分かります。
一般的に、対数関数 \(\large{y = \log_a x}\) と 指数関数 \(\large{y = a^x}\) には以下の関係があります。
\(\large{y=x}\) に関して対称となる
【2】対数のグラフの書き方の問題
本章では、対数のグラフの問題について解説します。
【2-1】問題(1) 底が1より大きい場合
まず、以下のような問題について考えます。
\(\displaystyle \large{y = \log_3 x}\)
対数関数のグラフを描くときは、『1. 特徴的な点の座標を何点か求める』、『2.漸近線の位置を求める』の2点から考えます。
まず、対数関数のグラフの特徴から、底が \(\large{a}\) であるとき、点\(\large{(1,0)}\)と点\(\large{(a,1)}\)を通ります。
底が \(\large{a=3}\) である場合、点\(\large{(1,0)}\)と点\(\large{(3,1)}\) となります。
また、2点だけではグラフを書くことは難しいので、\(\large{x=a^2}\) や \(\large{x=\frac{1}{a}}\)の座標を使います。
対数の公式から、
$$\large{y=\log_a a^2 = 2}$$
であるので、底が \(\large{a=3}\) である場合、点\(\large{(9,2)}\) となります。
また、
$$\large{y=\log_a \frac{1}{a} = -1}$$
であるので、底が \(\large{a=\frac{1}{3}}\) である場合、点\(\large{(\frac{1}{3},-1)}\) となります。
また、与えられたグラフは対数関数の性質から、\(\large{y}\)軸が漸近線となります。
以上から\(\large{y = \log_3 x}\) のグラフを描くと、下図のようになります。
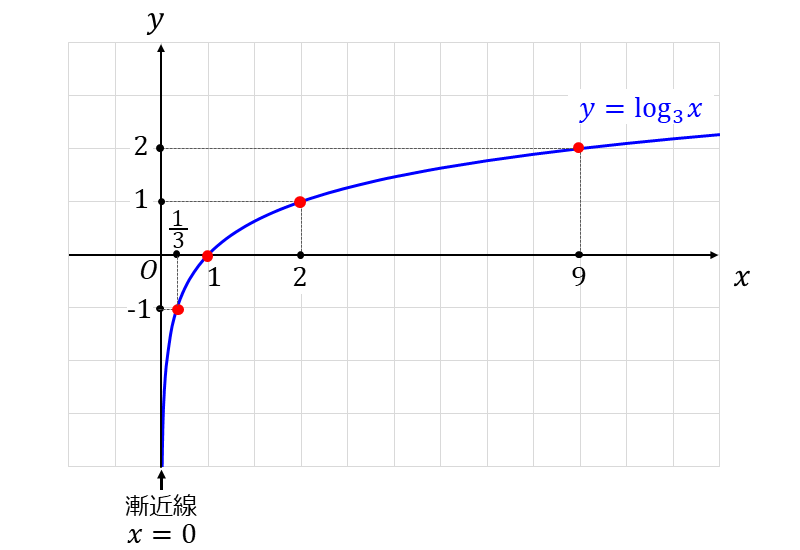
【2-2】問題(2) 底が1より小さい場合
次に、以下のような問題について考えます。
\(\displaystyle \large{y = \log_\frac{1}{3} {(x-2)}}\)
先述したように、対数関数のグラフを描くときは、『1. 特徴的な点の座標を何点か求める』、『2.漸近線の位置を求める』の2点から考えます。
まず、\(\large{y=\log_a x}\)は、対数関数のグラフの特徴から、点\(\large{(1,0)}\)と点\(\large{(a,1)}\)を通りますが、問題の関数は \(\large{y=\log_a (x-2)}\) より \(\large{x}\)軸方向に\(\large{+2}\)だけ平行移動しているため、点\(\large{(3,0)}\)と点\(\large{(a+2,1)}\)を通ります。
実際に \(\large{x=3}\)、\(\large{x=\frac{1}{3}+2}\) の \(\large{y}\)座標を計算すると、 $$\large{y=\log_\frac{1}{3} {(3-2)}=\log_\frac{1}{3} 1=0}$$ $$\large{y=\log_\frac{1}{3} {(\frac{1}{3}+2-2)}=\log_\frac{1}{3} \frac{1}{3}=1}$$ より、点\(\large{(3,0)}\)と点\(\large{(\frac{7}{3},1)}\)を通ることが分かります。
その他に、\(\large{y}\) の値が整数となる値を選んで座標を求めます。
\(\large{x=3+2 =5}\)から、 $$\large{y=\log_\frac{1}{3} {(5-2)} = \log_\frac{1}{3} 3 = -1}$$ \(\large{x=9+2 =11}\)から、 $$\large{y=\log_\frac{1}{3} {(11-2)} = \log_\frac{1}{3} 9 = -2}$$ より、点\(\large{(5,-1)}\)と点\(\large{(11,-2)}\)を通ることが分かります。
また、漸近線は \(\large{x}\)軸方向に\(\large{+2}\)だけ移動すると考えると、\(\large{x=2}\) となります。
以上から\(\large{y = \log_\frac{1}{3} x}\) のグラフを描くと、下図のようになります。

【2-3】問題(3) 底が1より小さい場合 | 対称移動
次に、以下のような問題について考えます。
\(\displaystyle \large{y = \log_\frac{1}{3} {\frac{1}{x-2}}}\)
真数が分数になっているため、対数の公式から整理すると、 $$\large{\log_\frac{1}{3} {\frac{1}{x-2}}=\log_\frac{1}{3}{(x-2)}^{-1}=-\log_\frac{1}{3}{(x-2)}}$$ となるため、問題(2)のグラフを \(\large{x}\)軸に関して対称移動すればよいことが分かります。
問題(2)で求めた座標を \(\large{x}\)軸に関して対称移動する場合、\(\large{y}\)座標の符号を反転させればよいので
点\(\large{(3,0)}\)、点\(\large{(\frac{7}{3},-1)}\)、点\(\large{(5,1)}\)と点\(\large{(11,2)}\)を通るグラフを描きます。
また、漸近線は \(\large{x}\)軸に関して対称移動しても変化しないため、\(\large{x=2}\) となります。
以上から\(\large{y = \log_\frac{1}{3} {\frac{1}{x-2}}}\) のグラフを描くと、下図のようになります。
