1/6公式 | 証明・使い方・面積の計算

本項では、『1/6公式の使い方や導出』 と 『問題の解き方』について解説します。

【1】1/6公式とは

1/6公式 とは、\(\large{x\hspace{1pt}}\)の二次式の積分に成り立つ公式です。

1/6公式 を覚えておくと、『二次関数と直線で囲まれた面積』や『2つの二次関数で囲まれた面積』などの積分を瞬時に計算することができます。

・例題

【解答と解説】
二次関数\(\large{\hspace{2pt}y=(x+2)(x-3)}\) と \(\large{x\hspace{1pt}}\)軸 に囲まれた面積\(\large{\hspace{1pt}S\hspace{3pt}}\)を図示すると、以下のようになります。 二次関数 \(\large{y=(x+2)(x-3)}\) は \(\large{-2 \leqq x \leqq 3}\) において \(\large{y \leqq 0}\) であることから \(\large{x\hspace{1pt}}\)軸 に囲まれた面積\(\large{\hspace{1pt}S\hspace{3pt}}\)は $$\large{S =-\int_{-2}^3 (x+2)(x-3)\hspace{1pt}dx}$$ となります。

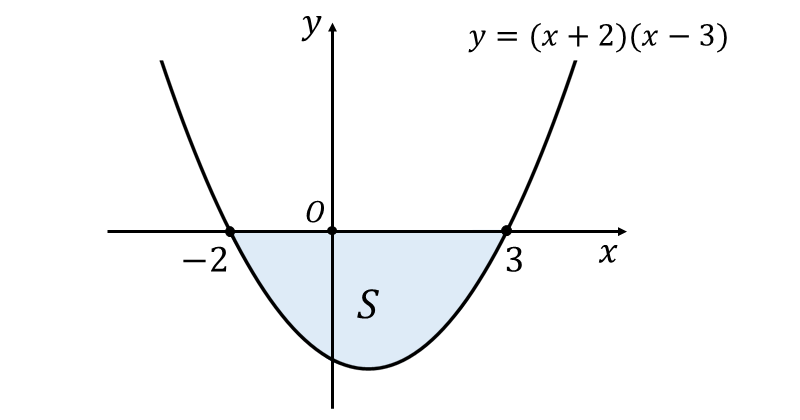
ここで、1/6公式から \begin{eqnarray} \large \int_{-2}^3 (x+2)(x-3)\hspace{1pt}dx &\large =&\large -\frac{1}{6}(3-(-2))^3 \\[0.5em] \large &\large =&\large -\frac{125}{6} \\ \end{eqnarray} したがって、求める面積\(\large{\hspace{1pt}S\hspace{1pt}}\)は、 $$\large{S = \frac{125}{6}}$$ 求められます。

・1/6公式の証明

1/6公式 $$\large{\displaystyle\large{\int_\alpha^\beta (x-\alpha)(x-\beta)\hspace{1pt}dx = -\frac{1}{6}(\beta-\alpha)^3}}$$ を証明します。

上式の左辺 \(\displaystyle\large{\int_\alpha^\beta (x-\alpha)(x-\beta)\hspace{1pt}dx}\) を以下のように変形します。

したがって、 $$\large{\displaystyle\large{\int_\alpha^\beta (x-\alpha)(x-\beta)\hspace{1pt}dx = -\frac{1}{6}(\beta-\alpha)^3}}$$ が導かれます。

【2】二次関数と直線で囲まれた面積

1/6公式の応用として、二次関数と直線で囲まれた面積の公式として使用することもできます。

二次関数 (\(\large{y=ax^2+bx+c}\)) と直線 (\(\large{y=px+q}\)) の交点を \(\large{x=\alpha,\hspace{2pt}\beta\hspace{3pt}}\) (\(\large{\alpha < \beta\hspace{1pt}}\)) とするとき、囲まれた面積は以下のように表されます。

上式から、『二次関数と直線の交点の値』 と 『二次の係数\(\large{\hspace{2pt}a\hspace{2pt}}\)の値』のみから面積を簡単に計算することができます。

・例題

【解答と解説】
二次関数 \(\large{y=3x^2-5x+3}\) と \(\large{y=4x-3}\) に囲まれた面積を図示すると、以下のようになります。 二次関数 \(\large{y=3x^2-5x+3}\) と \(\large{y=4x-3}\) の交点を求めると、 \begin{eqnarray} \large 3x^2-5x+3&\large =&\large 4x-3 \\[0.5em] \large 3x^2 -9x + 6 &\large =&\large 0 \\[0.5em] \large 3(x-1)(x-2) &\large =&\large 0 \\ \end{eqnarray} つまり、交点は \(\large{x=1\hspace{1pt},\hspace{1pt}2}\) となります。

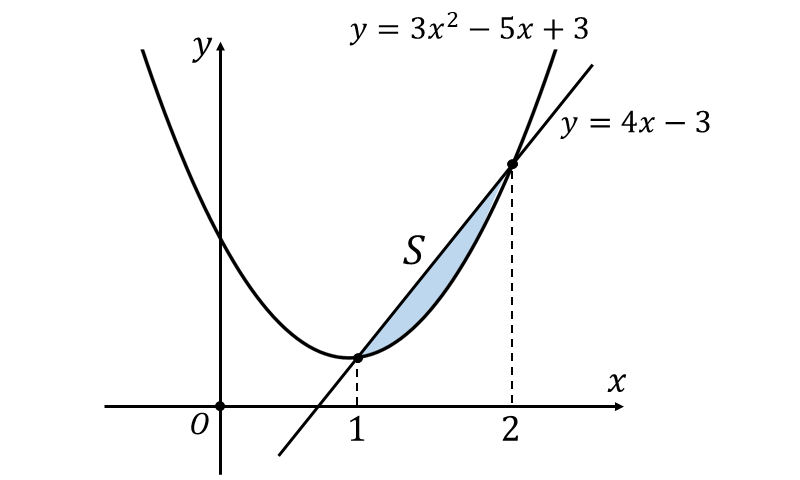
求める面積\(\large{\hspace{1pt}S}\) は、二次関数の二次の係数が \(\large{a=3}\)、交点が \(\large{x=1\hspace{1pt},\hspace{1pt}2}\) であることから \begin{eqnarray} \large S&\large =&\large \frac{|3|}{6}(2-1)^3 \hspace{1pt} dx\\[0.5em] \large &\large =&\large \frac{1}{2}\\ \end{eqnarray} と求められます。

・6分の1公式の証明 | 二次関数と直線

二次関数 \(\large{f(x)= a x^2 + bx + c}\)、直線 \(\large{g(x)=px+q}\) が交点 \(\large{x=\alpha,\hspace{2pt}\beta\hspace{3pt}}\) (\(\large{\alpha < \beta\hspace{1pt}}\)) を持つとき、囲まれた面積\(\large{\hspace{1pt}S\hspace{3pt}}\)が以下の式で表されることを示します。 $$\large{S = \frac{|a|}{6}(\beta-\alpha)^3}$$

\(\large{f(x)}\) と \(\large{g(x)}\) の交点が \(\large{x=\alpha,\hspace{2pt}\beta\hspace{3pt}}\) であるとき、\(\large{f(x)-g(x)=0}\) の解が \(\large{x=\alpha,\hspace{2pt}\beta\hspace{3pt}}\) であるため、 $$\large{f(x)-g(x)=a(x-\alpha)(x-\beta)}$$ と表せます。

ここで、二次関数 \(\large{f(x)}\)、直線 \(\large{g(x)}\) で囲まれる面積\(\large{\hspace{1pt}S\hspace{2pt}}\)は、以下のように表せます。 \begin{eqnarray} \large S &\large =& \large \int_\alpha^\beta \left|f(x)-g(x)\right|\hspace{1pt}dx \\[0.5em] \large &\large =&\large\int_\alpha^\beta \left| a(x-\alpha)(x-\beta)\right| \hspace{1pt}dx \\[0.5em] \large &\large =&\large |a| \int_\alpha^\beta \left|(x-\alpha)(x-\beta)\right| \hspace{1pt}dx \\[0.5em] \end{eqnarray} ここで、\(\large{\alpha \leqq x \leqq \beta}\) において \(\large{(x-\alpha)(x-\beta) \leqq 0}\) より $$\large{|(x-\alpha)(x-\beta)|=-(x-\alpha)(x-\beta)}$$ また、6/1公式から $$\large{\int_\alpha^\beta (x-\alpha)(x-\beta)\hspace{1pt}dx = -\frac{1}{6}(\beta-\alpha)^3}$$ であるため、 \begin{eqnarray} \large S &\large =& \large |a| \int_\alpha^\beta \left|(x-\alpha)(x-\beta)\right| \hspace{1pt}dx \\[0.5em] \large &\large =&\large |a| \int_\alpha^\beta \{- (x-\alpha)(x-\beta)\} \hspace{1pt}dx \\[0.5em] \large &\large =&\large \frac{|a|}{6}(\beta-\alpha)^3 \\[0.5em] \end{eqnarray} となります。 したがって、二次関数 \(\large{f(x)= a x^2 + bx + c}\)、直線 \(\large{g(x)=px+q}\) が交点 \(\large{x=\alpha,\hspace{2pt}\beta\hspace{3pt}}\) (\(\large{\alpha < \beta\hspace{1pt}}\)) を持つとき、囲まれた面積\(\large{\hspace{1pt}S\hspace{2pt}}\)は $$\large{S = \frac{|a|}{6}(\beta-\alpha)^3}$$ となります。

【3】1/6公式 | 2つの二次関数に囲まれた面積

\(\large{2\hspace{1pt}}\)つの二次関数 \(\large{y= a_1 x^2 + b_1 x + c_1}\) と \(\large{y=a_2 x^2 + b_2 x + c_2}\) が交点 \(\large{x=\alpha,\hspace{2pt}\beta\hspace{3pt}}\) (\(\large{\alpha < \beta\hspace{1pt}}\)) を持つとき、囲まれた面積\(\large{\hspace{1pt}S\hspace{2pt}}\)は以下の式で表されます。

上式から、『\(\large{2\hspace{1pt}}\)つの二次関数の交点の値』 と 『二次の係数の差分の絶対値\(\large{\hspace{2pt}|a_1-a_2|\hspace{2pt}}\)』のみから面積を簡単に計算することができます。

・例題

【解答と解説】
二次関数 \(\large{y=2x^2-5x-5}\) と \(\large{y=-2x^2+3x+7}\) に囲まれた面積を図示すると、以下のようになります。 二次関数 \(\large{y=2x^2-5x-5}\) と \(\large{y=-2x^2+3x+7}\) の交点を求めると、 \begin{eqnarray} \large 2x^2-5x-5&\large =&\large -2x^2+3x+7 \\[0.5em] \large 4x^2 -8x - 12 &\large =&\large 0 \\[0.5em] \large 4(x+1)(x-3) &\large =&\large 0 \\ \end{eqnarray} つまり、交点は \(\large{x=-1\hspace{1pt},\hspace{1pt}3}\) となります。

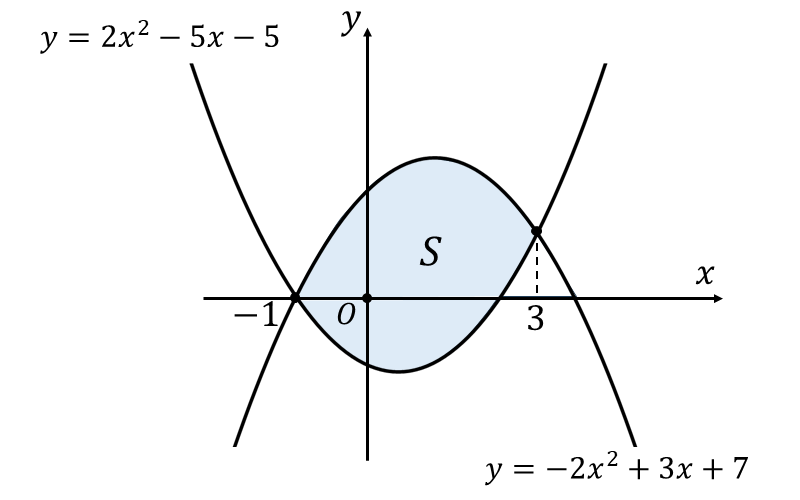
二次関数の係数がそれぞれ \(\large{a_1=2\hspace{1pt},\hspace{2pt}a_2=-2}\)、交点が \(\large{x=-1\hspace{1pt},\hspace{1pt}3}\) であることから 求める面積\(\large{\hspace{1pt}S}\) は \begin{eqnarray} \large S &\large =&\large\frac{|2-(-2)|}{6}(3-(-1))^3\\[0.5em] \large &\large =&\large \frac{128}{3}\\[0.5em] \end{eqnarray} と求められます。

・6分の1公式の証明 | 2つの二次関数に囲まれた面積

二次関数 \(\large{f(x)= a_1 x^2 + b_1 x + c_1}\) と \(\large{g(x)=a_2 x^2 + b_2 x + c_2}\) が交点 \(\large{x=\alpha,\hspace{2pt}\beta\hspace{3pt}}\) (\(\large{\alpha < \beta\hspace{1pt}}\)) を持つとき、囲まれた面積\(\large{\hspace{1pt}S\hspace{2pt}}\)が以下の式で表されることを示します。 $$\large{S = \frac{|a_1-a_2|}{6}(\beta-\alpha)^3}$$

\(\large{f(x)}\) と \(\large{g(x)}\) の交点が \(\large{x=\alpha,\hspace{2pt}\beta\hspace{3pt}}\) であるとき、\(\large{f(x)-g(x)=0}\) の解が \(\large{x=\alpha,\hspace{2pt}\beta\hspace{3pt}}\) であるため、 $$\large{f(x)-g(x)=(a_1-a_2)(x-\alpha)(x-\beta)}$$ と表せます。

ここで、二次関数 \(\large{f(x)\hspace{1pt},\hspace{2pt}g(x)}\) で囲まれる面積\(\large{\hspace{1pt}S\hspace{2pt}}\)は、以下のように表せます。 \begin{eqnarray} \large S &\large =& \large \int_\alpha^\beta |f(x)-g(x)|\hspace{1pt}dx \\[0.5em] \large &\large =&\large \int_\alpha^\beta |(a_1-a_2)(x-\alpha)(x-\beta)| \hspace{1pt}dx \\[0.5em] \large &\large =&\large |a_1-a_2|\int_\alpha^\beta |(x-\alpha)(x-\beta)| \hspace{1pt}dx \\[0.5em] \end{eqnarray} ここで、\(\large{\alpha \leqq x \leqq \beta}\) において \(\large{(x-\alpha)(x-\beta) \leqq 0}\) より $$\large{|(x-\alpha)(x-\beta)|=-(x-\alpha)(x-\beta)}$$ 1/6公式から $$\large{\int_\alpha^\beta (x-\alpha)(x-\beta)\hspace{1pt}dx = -\frac{1}{6}(\beta-\alpha)^3}$$ であるため、 \begin{eqnarray} \large S &\large =& \large |a_1-a_2| \int_\alpha^\beta \left|(x-\alpha)(x-\beta)\right| \hspace{1pt}dx \\[0.5em] \large &\large =&\large |a_1-a_2| \int_\alpha^\beta \{- (x-\alpha)(x-\beta)\} \hspace{1pt}dx \\[0.5em] \large &\large =&\large \frac{|a_1-a_2|}{6}(\beta-\alpha)^3 \\[0.5em] \end{eqnarray} となります。 したがって、二次関数 \(\large{f(x)= a_1 x^2 + b_1 x + c_1}\) と \(\large{g(x)=a_2 x^2 + b_2 x + c_2}\) が交点 \(\large{x=\alpha,\hspace{2pt}\beta\hspace{3pt}}\) (\(\large{\alpha < \beta\hspace{1pt}}\)) を持つとき、囲まれた面積\(\large{\hspace{1pt}S\hspace{2pt}}\)は $$\large{S = \frac{|a_1-a_2|}{6}(\beta-\alpha)^3}$$ となります。

【4】問題と解き方

本章では、1/6公式 に関連した問題について解説します。

(解答と解説 : 問題(1) 問題(2) )

問題(1) | 二次関数と直線に囲まれた面積の最小値

二次関数 \(\large{y=x^2+2x-3}\) と 直線 \(\large{y=mx +2}\) に囲まれた面積を図示すると、以下のようになります。 まず、二次関数 \(\large{y=x^2+2x-3}\) と 直線 \(\large{y=mx +2}\) が\(\large{\hspace{1pt}2\hspace{2pt}}\)つの交点を持つための条件を求めます。

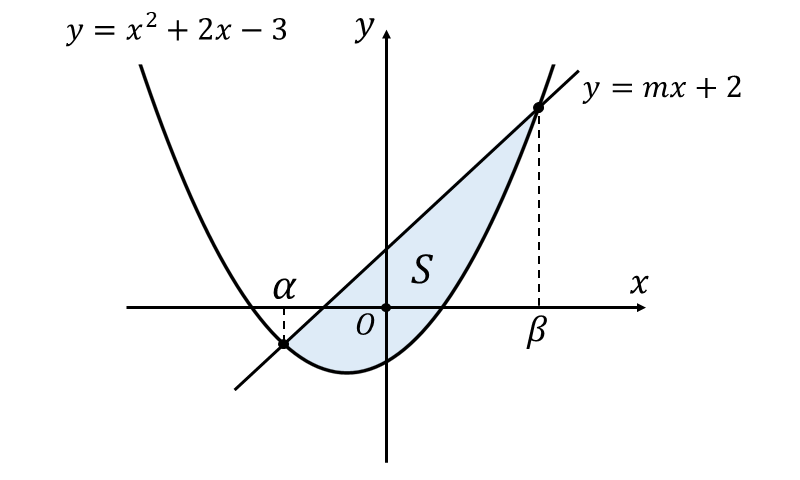
二次関数 と 直線 の式から 交点の\(\large{x\hspace{1pt}}\)座標の満たす式を求めると、 \begin{eqnarray} \large x^2+2x-3 &\large = &\large mx +2\\[0.5em] \large x^2+(2-m)x-5 &\large =&\large 0\\[0.5em] \end{eqnarray} となります。上式の判別式を計算すると $$\large{D = (2-m)^2 +20 > 0}$$ であるため、問題の二次関数と直線は すべての\(\large{\hspace{1pt}m\hspace{2pt}}\)に対して\(\large{\hspace{1pt}2\hspace{1pt}}\)つの交点を持ちます。

二次関数 \(\large{y=x^2+2x-3}\) と 直線 \(\large{y=mx +2}\) の交点の \(\large{x\hspace{1pt}}\)座標を \(\large{x=\alpha,\hspace{2pt}\beta\hspace{3pt}}\) とすると 二次関数と直線で囲まれた面積の公式から、面積\(\large{\hspace{1pt}S\hspace{2pt}}\)は以下のようになります。 \begin{eqnarray} \large S &\large =&\large\frac{|1|}{6}(\beta - \alpha)^3\\[0.5em] \large &\large =&\large \frac{1}{6}(\beta - \alpha)^3\\[0.5em] \end{eqnarray}

ここで \(\large{\beta\hspace{1pt},\hspace{2pt}\alpha}\) は、\(\large{ x^2+(2-m)x-5 = 0}\) の解であるため、解の公式から \begin{eqnarray} \large \beta - \alpha &\large =&\large \frac{-(2-m)+\sqrt{D}}{2}-\frac{-(2-m)-\sqrt{D}}{2}\\[0.5em] \large &\large =&\large \sqrt{D}\\[0.5em] \large &\large =&\large \sqrt{(2-m)^2 +20}\\[0.5em] \end{eqnarray} よって、\(\large{m=2}\) のとき \(\large{\beta - \alpha}\) は最小値 \(\large{2\sqrt{5}}\) となります。

したがって、このときの面積\(\large{S\hspace{1pt}}\)が \begin{eqnarray} \large S &\large =&\large \frac{1}{6}(2\sqrt{5})^3\\[0.5em] \large &\large =&\large \frac{20\sqrt{5}}{3}\\[0.5em] \end{eqnarray} であることから、\(\large{m=2}\) のとき 最小値 \(\displaystyle\large{\frac{20\sqrt{5}}{3}}\) となります。

問題(2) | 2つの二次関数に囲まれた面積の最小値

二次関数 \(\large{y=2x^2+mx-2}\) と \(\large{y=-2x^2+3x+1}\) に囲まれた面積を図示すると、以下のようになります。 まず、二次関数 \(\large{y=2x^2+mx-2}\) と \(\large{y=-2x^2+3x+1}\) が \(\large{2\hspace{1pt}}\)つの交点を持つための条件を求めます。

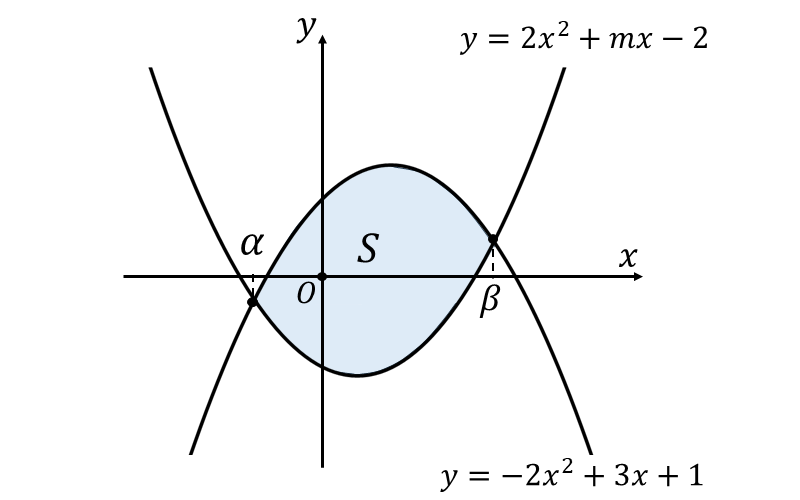
\(\large{2\hspace{1pt}}\)つの式から 交点の\(\large{x\hspace{1pt}}\)座標の満たす式を求めると、 \begin{eqnarray} \large 2x^2+mx-2 &\large = &\large -2x^2+3x+1\\[0.5em] \large 4x^2+(m-3)x-3 &\large =&\large 0\\[0.5em] \end{eqnarray} となります。

上式の判別式を計算すると $$\large{D = (m-3)^2 +48 > 0}$$ であるため、問題の\(\large{2\hspace{1pt}}\)つの二次関数は すべての\(\large{\hspace{1pt}m\hspace{2pt}}\)に対して\(\large{\hspace{1pt}2\hspace{1pt}}\)つの交点を持ちます。

二次関数 \(\large{y=2x^2+mx-2}\) と \(\large{y=-2x^2+3x+1}\) の交点の \(\large{x\hspace{1pt}}\)座標を \(\large{x=\alpha,\hspace{2pt}\beta\hspace{3pt}}\) とすると 2つの二次関数に囲まれた面積の公式から、面積\(\large{\hspace{1pt}S\hspace{2pt}}\)は以下のようになります。 \begin{eqnarray} \large S &\large =&\large\frac{|2-(-2)|}{6}(\beta - \alpha)^3\\[0.5em] \large &\large =&\large \frac{2}{3}(\beta - \alpha)^3\\[0.5em] \end{eqnarray}

ここで \(\large{\beta\hspace{1pt},\hspace{2pt}\alpha}\) は、\(\large{ 4x^2+(m-3)x-3 = 0}\) の解であるため、解の公式から \begin{eqnarray} \large \beta - \alpha &\large =&\large \frac{-(m-3)+\sqrt{D}}{8}-\frac{-(m-3)-\sqrt{D}}{8}\\[0.5em] \large &\large =&\large \frac{\sqrt{D}}{4}\\[0.5em] \large &\large =&\large \frac{\sqrt{(m-3)^2 +48}}{4}\\[0.5em] \end{eqnarray} よって、\(\large{m=3}\) のとき \(\large{\beta - \alpha}\) は最小値 \(\large{\sqrt{3}}\) となります。

したがって、このときの面積\(\large{S\hspace{1pt}}\)が \begin{eqnarray} \large S &\large =&\large \frac{2}{3}(\sqrt{3})^3\\[0.5em] \large &\large =&\large 2\sqrt{3}\\[0.5em] \end{eqnarray} であることから、\(\large{m=3}\) のとき 最小値 \(\displaystyle\large{2\sqrt{3}}\) をとります。