増減表の作り方
本項では、『増減表の作り方』 と 『問題の解き方』について解説します。
【1】増減表の作り方
増減表とは、関数の『定義域・増減・極値・凹凸・変曲点』などを一覧でまとめる表のことです。
増減表を作ることで、グラフを描くための情報を簡単に整理できるようになります。
本章では、まず増減表を作るときの基本となる 関数の増減 と 極大値・極小値 の調べ方について説明します。
・関数の増減の調べ方
関数\(\large{\hspace{1pt}f(x)}\) の増減 すなわち 『グラフが右上がりか、右下がりか』を調べるには 関数\(\large{\hspace{1pt}f(x)}\) を微分した \(\large{f'(x)}\) の符号を確認します。
ここで、\(\large{f'(x)}\) の符号 と 関数の増減には以下のような対応関係があります。
・\(\large{f'(x)>0}\) の場合、\(\large{f(x)\hspace{1pt}}\)は単調に増加 (右上がりのグラフ)
・\(\large{f'(x)< 0 }\) の場合、\(\large{f(x)\hspace{1pt}}\)は単調に減少 (右下がりのグラフ)
・\(\large{f'(x) = 0 }\) の場合、関数は一定
増減表を作るときは、まず \(\large{f'(x) = 0 }\) を満たす \(\large{x}\) を求めます。
次に \(\large{f'(x) = 0 }\) を満たす \(\large{x}\) を境界として \(\large{f'(x) }\) の符号を確認することで、関数の増減を調べます。
・極大値と極小値の調べ方
関数\(\large{\hspace{1pt}f(x)}\) の極大値と極小値では \(\large{f'(x)=0}\) となり、その前後で \(\large{f'(x)}\) の符号が変化します。
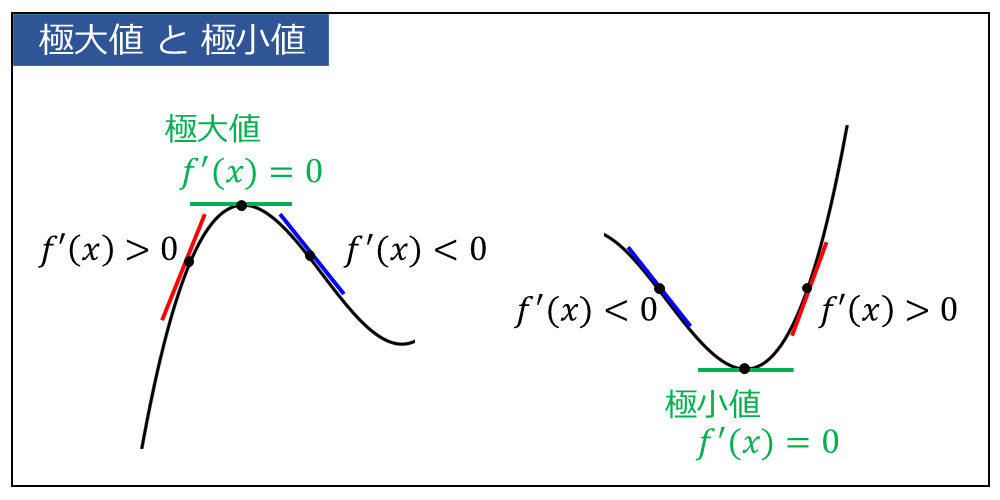
したがって、極大値と極小値を求めるためには \(\large{f'(x) = 0 }\) を満たす \(\large{x}\) の前後で \(\large{f'(x) }\) の符号がどのように変化するかを確認します。
・\(\large{x=a}\) の前後で \(\large{f'(x)}\) の符号が
正から負に変化するとき、\(\large{f(a)}\) は極大値
・\(\large{x=a}\) の前後で \(\large{f'(x)}\) の符号が
負から正に変化するとき、\(\large{f(a)}\) は極小値
・増減表の例題
関数の増減や極大値・極小値から増減表を作る例として、三次関数の問題について考えます。
\(\displaystyle \large{f(x)=2x^3-6x}\)
まず、関数 \(\displaystyle \large{f(x)=2x^3-6x}\) を微分すると、 $$\large{f'(x)=6x^2-6}$$ となります。
\(\large{f'(x)=0}\) を解くと、 \begin{eqnarray} \large 6x^2-6 &\large =&\large 0\\[0.5em] \large x^2 &\large =&\large 1\\[0.5em] \large x &\large =&\large \pm 1\\[0.5em] \end{eqnarray}
ここで、\(\large{x=\pm 1}\) の前後における \(\displaystyle\large{f'(x)}\) の符号の変化を調べます。
\(\large{f'(x)=6x^2-6}\) より
\(\large{x < -1}\) のとき \(\large{f'(x)>0}\)
\(\large{-1 < x < 1\hspace{2pt}}\) のとき \(\large{f'(x)< 0}\)
\(\large{ x > 1}\) のとき \(\large{f'(x) > 0}\)
となります。
よって、関数 \(\displaystyle \large{f(x)}\) は、\(\large{x=-1}\) で極大値、\(\large{x=1}\) で極小値をとります。
以上から、増減表を作ると 以下のようになります。
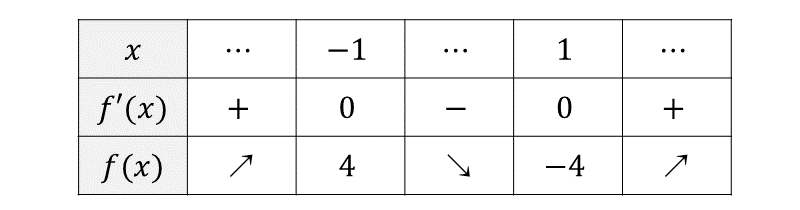
増減表の二行目には \(\large{f'(x)}\) の符号、三行目には 極大値・極小値の値を入れます。
また、グラフの概形が分かりやすいように、矢印の記号で関数の増減を示します。
この増減表からグラフを描くと、以下のようになります。
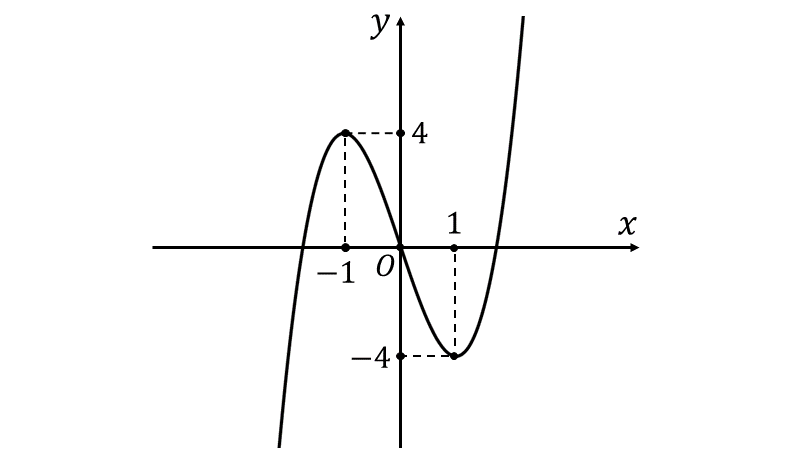
・増減表の作り方のまとめ
例題の増減表の作り方を整理すると、以下のようになります。
2. \(\large{f'(x)=0}\) を満たす \(\large{x}\) を求める
3. \(\large{f'(x)}\) の符号の変化を調べる
5. 二行目に \(\large{f'(x)}\) の符号を 『+,-,0』で記入
6. 三行目に 極小値・極大値
と \(\large{f(x)}\) の接線の傾きを矢印の記号で記入
【2】グラフの凹凸 と 変曲点
関数の増減や極大値・極小値に加え、『 グラフの凹凸 と 変曲点 』を調べることでより正確にグラフを描くことができます。
・なぜ凹凸を調べるのか
例題(1)の関数の増減のみを調べた増減表を以下に示します。
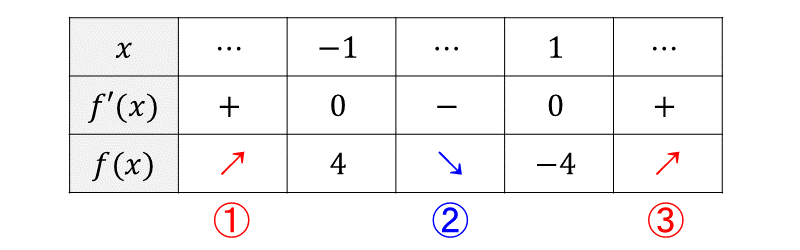
この増減表からグラフを描くと、以下のようになります。
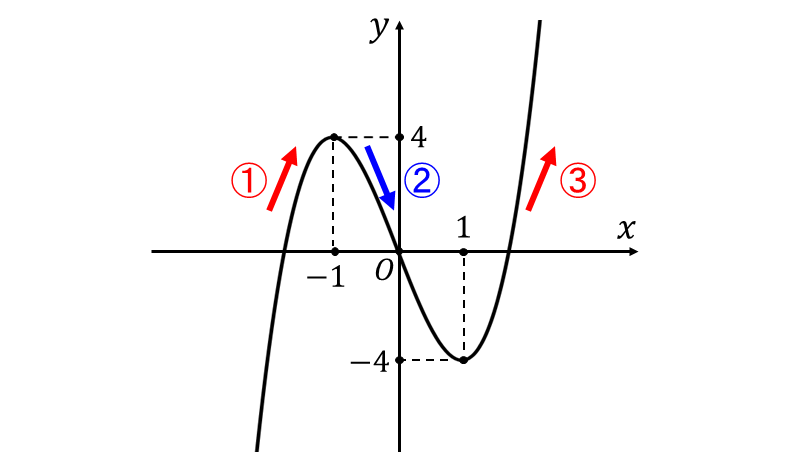
増減表から①と③の区間では 『\(\large{x}\) が増加すると\(\large{y}\) が増加する』ことが分かります。
しかし、実際のグラフでは ①の区間は『\(\large{x}\) が増加すると\(\large{y}\) が増加する かつ 増加する割合が減る(上に凸)』となります。
また、③の区間 は『\(\large{x}\) が増加すると\(\large{y}\) が増加する かつ 増加する割合が増える(下に凸)』となります。
つまり、同じ右上がりのグラフでも、増加の仕方が変わることになります。
そのため、正確にグラフを描くためには関数の増減だけでなく、グラフの凹凸まで調べる必要があります。
・グラフの凹凸
関数\(\large{\hspace{1pt}f(x)}\) のグラフの凹凸は、\(\large{f''(x)}\) の符号を調べることで分かります。
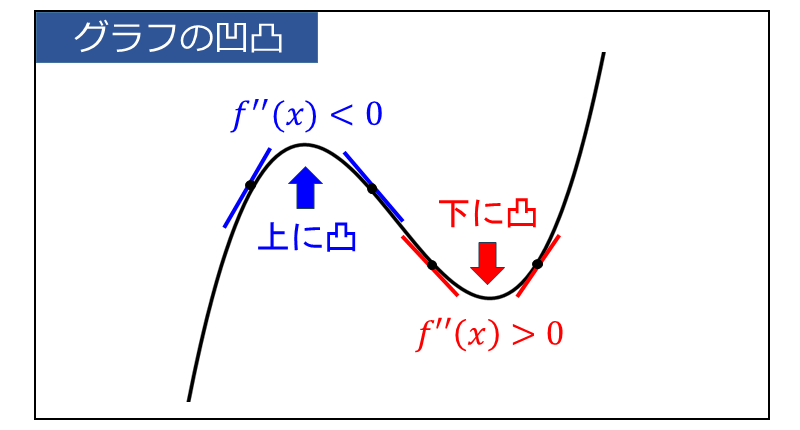
・\(\large{f''(x)>0}\) の区間は グラフが下に凸
・\(\large{f''(x) < 0}\) の区間は グラフが上に凸
下図のように、\(\large{f''(x)>0}\) の区間は 接線の傾きが増加する割合が増えるため、下に凸の形状となります。
一方、\(\large{f''(x) < 0}\) の区間は 接線の傾きの増加する割合が減るため、上に凸の形状となります。
・変曲点
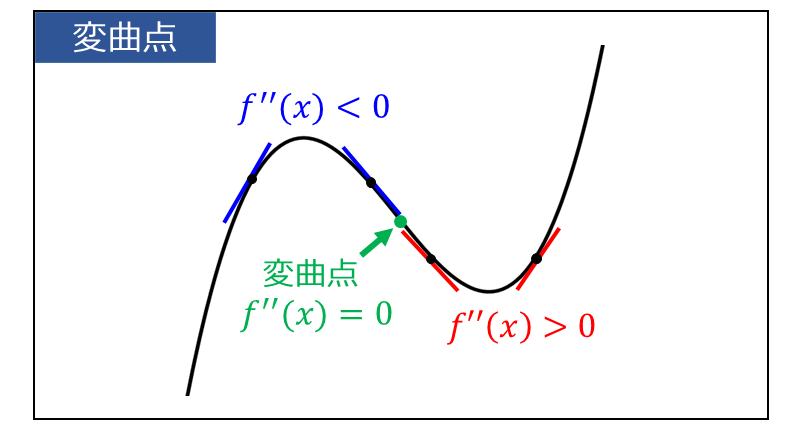
関数\(\large{\hspace{1pt}f(x)}\) の変曲点とは、グラフの凹凸の変化する境界のことをいいます。
変曲点は関数\(\large{\hspace{1pt}f(x)}\) の二次導関数 \(\large{f''(x)}\) の符号の変化を調べることで分かります。
下図のように \(\large{f''(x)=0}\) となる変曲点で グラフの凹凸の形状が変化します。
・増減表の例題
関数の凹凸や変曲点を調べて増減表を作る例として、三次関数の問題について考えます。
を調べ、増減表を作れ
\(\displaystyle \large{f(x)=2x^3-6x}\)
例題(1)で \(\displaystyle \large{f(x)=2x^3-6x}\) の増減と極大値・極小値を調べた増減表を作成しました。

本問では、この続きとして 凹凸, 変曲点 を調べて増減表を作成します。
まず、関数 \(\displaystyle \large{f(x)=2x^3-6x}\) の二次導関数 \(\large{f''(x)}\) を求めると $$\large{f'(x)=6x^2-6}$$ $$\large{f''(x)=12x}$$ となります。
\(\large{f''(x)=0}\) を解くと、\(\large{x=0}\) となります。
ここで、\(\large{x=0}\) の前後における \(\displaystyle\large{f''(x)}\) の符号の変化を調べます。
\(\large{f''(x)=12x}\) より
\(\large{x < 0}\) のとき \(\large{f''(x)< 0}\)
\(\large{x > 0 }\) のとき \(\large{f''(x) > 0}\)
となります。
よって、関数 \(\displaystyle \large{f(x)}\) は、\(\large{x=0}\) で変曲点をとります。
以上から、増減表を作ると 以下のようになります。
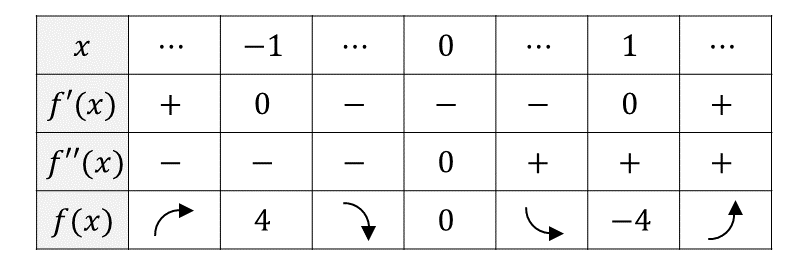
増減表の三行目には \(\large{f''(x)}\) の符号を『+,-,0』で記入します。
また、グラフの凹凸まで調べた増減表では、増減と凹凸の両方が分かりやすいように丸い矢印の記号を記入します。
【3】問題と解き方
本章では、増減表の作り方 に関連した問題について解説します。
を調べ、増減表を作れ
\(\displaystyle \large{f(x)=x^4-2x^2}\)
を調べ、増減表を作れ
\(\displaystyle \large{f(x)= \frac{\log x}{x}}\)
問題(1) 四次関数の増減表
を調べ、増減表を作れ
\(\displaystyle \large{f(x)=x^4-2x^2}\)
【解答と解説】
本問は、四次関数の増減表を作る問題です。
まず、関数 \(\displaystyle \large{f(x)=x^4-2x^2}\) を微分して、極値の座標の候補を求めます。
\(\displaystyle\large{f(x)=x^4-2x^2}\) のとき、\(\displaystyle\large{f'(x)=4x^3-4x}\) となります。
\(\large{f'(x)=0}\) を解くと、 \begin{eqnarray} \large 4x^3-4x &\large =&\large 0\\[0.5em] \large 4x(x^2-1) &\large =&\large 0\\[0.5em] \large 4x(x+1)(x-1) &\large =&\large 0\\[0.5em] \end{eqnarray}
したがって、\(\large{x=-1,\hspace{2pt}0,\hspace{2pt}1}\) のとき \(\large{f'(x)=0}\) となります。
ここで、\(\displaystyle\large{f'(x)}\) の符号を調べます。
\(\large{x < -1}\) のとき \(\large{f'(x) < 0}\)
\(\large{-1 < x < 0}\) のとき \(\large{f'(x) > 0}\)
\(\large{0 < x < 1}\) のとき \(\large{f'(x) < 0}\)
\(\large{ x > 1}\) のとき \(\large{f'(x) > 0}\)
以上から、関数 \(\displaystyle \large{f(x)}\) は、\(\large{x=-1,\hspace{1pt}1}\) で極小値、\(\large{x=0}\) で極大値をとります。
次に、関数 \(\displaystyle \large{f'(x)=4x^3-4x}\) を微分して、変曲点の座標の候補を求めます。
\(\displaystyle\large{f'(x)=4x^3-4x}\) のとき、\(\displaystyle\large{f''(x)=12x^2-4}\) となります。
\(\large{f''(x)=0}\) を解くと、 \begin{eqnarray} \large 12x^2-4 &\large =&\large 0\\[0.5em] \large x^2 &\large =&\large \frac{1}{3}\\[0.5em] \large x &\large =&\large \pm \frac{1}{\sqrt{3}}\\[0.5em] \end{eqnarray}
ここで、\(\displaystyle\large{f''(x)}\) の符号を調べます。
\(\displaystyle\large{x < -\frac{1}{\sqrt{3}}}\) のとき \(\large{f''(x) > 0}\)
\(\displaystyle\large{-\frac{1}{\sqrt{3}} < x < \frac{1}{\sqrt{3}}}\) のとき \(\large{f''(x) < 0}\)
\(\displaystyle\large{ x > \frac{1}{\sqrt{3}}}\) のとき \(\large{f''(x) > 0}\)
以上から、関数 \(\displaystyle \large{f(x)}\) は、\(\displaystyle\large{x=-\frac{1}{\sqrt{3}},\hspace{1pt}\frac{1}{\sqrt{3}}}\) に変曲点を持ちます。
したがって、増減表を作ると 以下のようになります。
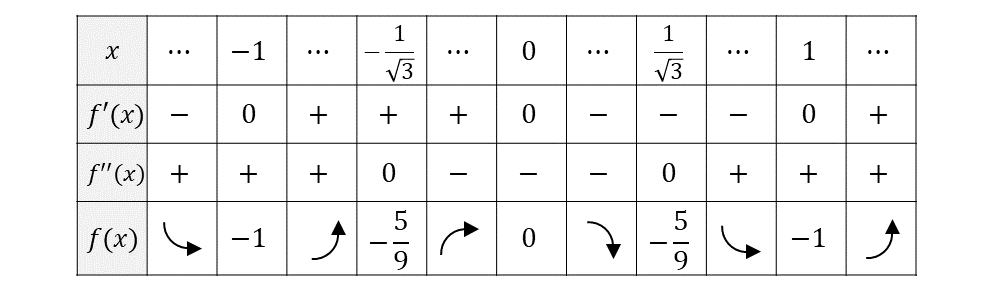
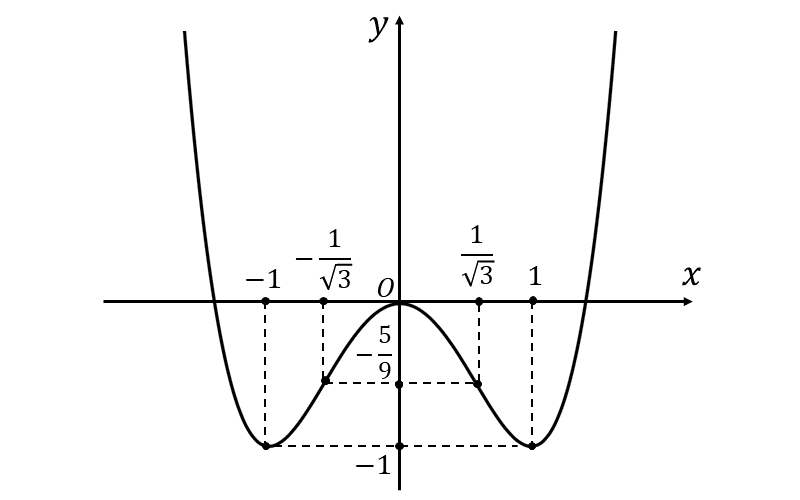
また、問題の四次関数のグラフは、以下のようになります。
問題(2) 対数関数を含む関数の増減表
を調べ、増減表を作れ
\(\displaystyle \large{f(x)=\frac{\log x}{x}}\)
【解答と解説】
本問は、対数関数を含む関数の増減表を作る問題です。
まず、対数の真数条件から \(\large{x}\) の定義域は \(\large{x>0}\) となります。
問題の関数は、自然対数の微分 $$\large{(\log x)' = \frac{1}{x}}$$ と、商の微分公式 $$\large{\left\{\frac{f(x)}{g(x)}\right\}' = \frac{f'(x)g(x)-f(x)g'(x)}{\{g(x)\}^2}}$$ を利用して微分します。
関数 \(\displaystyle \large{f(x)=\frac{\log x}{x}}\) を微分して、極値の座標の候補を求めます。
商の微分公式から、 \begin{eqnarray} \large f'(x) &\large =&\large \frac{(\log x)'\cdot x - \log x \cdot (x)'}{x^2}\\[0.5em] \large &\large =&\large \frac{\frac{1}{x} \cdot x - \log x \cdot 1}{x^2}\\[0.5em] \large &\large =&\large \frac{1 - \log x }{x^2}\\[0.5em] \end{eqnarray} となります。
\(\large{f'(x)=0}\) を解くと、 \begin{eqnarray} \large 1 - \log x &\large =&\large 0\\[0.5em] \large \log x &\large =&\large 1 \\[0.5em] \large x &\large =&\large e\\[0.5em] \end{eqnarray}
したがって、\(\large{x=e}\) のとき \(\large{f'(x)=0}\) となります。
ここで、\(\displaystyle\large{f'(x)}\) の符号を調べます。
\(\large{0 < x < e}\) のとき \(\large{f'(x) > 0}\)
\(\large{ x > e}\) のとき \(\large{f'(x) < 0}\)
以上から、関数 \(\displaystyle \large{f(x)}\) は、\(\large{x=e }\) で極大値をとります。
次に、関数 \(\displaystyle \large{f'(x)=\frac{1 - \log x }{x^2}}\) を微分して、変曲点の座標の候補を求めます。
商の微分公式から、 \begin{eqnarray} \large f''(x) &\large =&\large \frac{(1 - \log x)'\cdot x^2 - (1 - \log x)\cdot (x^2)'}{x^4}\\[0.5em] \large &\large =&\large \frac{( - \frac{1}{x})\cdot x^2 - (1 - \log x)\cdot (2x)}{x^4}\\[0.5em] \large &\large =&\large \frac{2\log x -3 }{x^3}\\[0.5em] \end{eqnarray} となります。
\(\large{f''(x)=0}\) を解くと、 \begin{eqnarray} \large 2\log x -3 &\large =&\large 0\\[0.5em] \large \log x &\large =&\large \frac{3}{2}\\[0.5em] \large x &\large =&\large e^{\frac{3}{2}}\\[0.5em] \end{eqnarray}
ここで、\(\displaystyle\large{f''(x)}\) の符号を調べます。
\(\displaystyle\large{0 < x < e^{\frac{3}{2}}}\) のとき \(\large{f''(x) < 0}\)
\(\displaystyle\large{ x > e^{\frac{3}{2}}}\) のとき \(\large{f''(x) > 0}\)
以上から、関数 \(\displaystyle \large{f(x)}\) は、\(\displaystyle\large{x=e^{\frac{3}{2}}}\) に変曲点を持ちます。
したがって、増減表を作ると 以下のようになります。
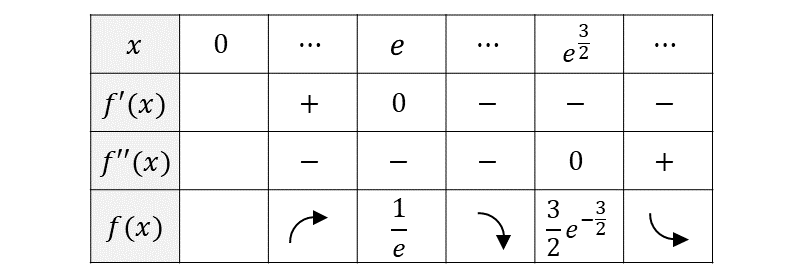
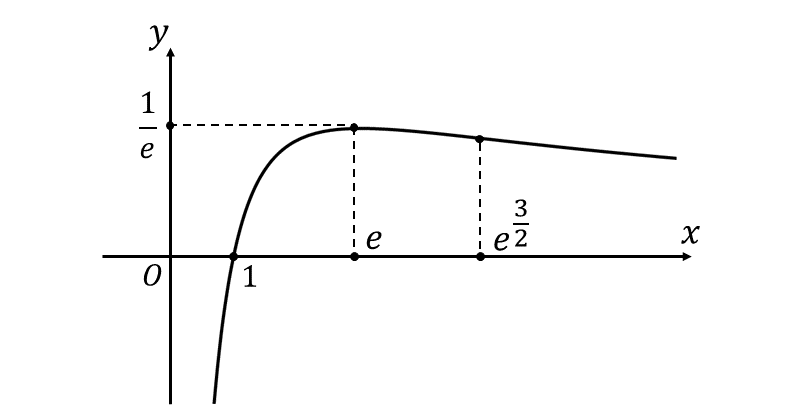
また、問題のグラフは以下のようになります。