-光と光学に関連する用語の解説サイト-

円の面積を求める積分

本項では、『円の面積を求める積分』と『関連する問題』について解説します。

1. 円の面積を求める積分
- ・積分の計算方法
2. 問題と解き方

【1】円の面積を求める積分

以下のような定積分を解く問題について考えます。

問題

$\large{a\hspace{1pt}}$を正の定数とするとき、次の定積分を求めよ
$\displaystyle \large{ \int_{-a}^a \sqrt{a^2-x^2} \hspace{1pt} dx}$

関数 $\large{y=\sqrt{a^2-x^2} }$ の両辺を二乗すると、 \begin{eqnarray} \large y^2 &\large =&\large (\sqrt{a^2 - x^2})^2 \\[0.5em] \large &\large =&\large a^2 - x^2\\[0.5em] \end{eqnarray} すなわち、 $$\large{x^2 + y^2 = a^2}$$ と変形されることから、関数 $\large{y=\sqrt{a^2-x^2} }$ は半径$\large{a\hspace{2pt}}$の円の上半分を表します。
( $\large{y=\sqrt{a^2-x^2} }$ を二乗していることから、$\large{y \geqq 0}$ の範囲となります。)

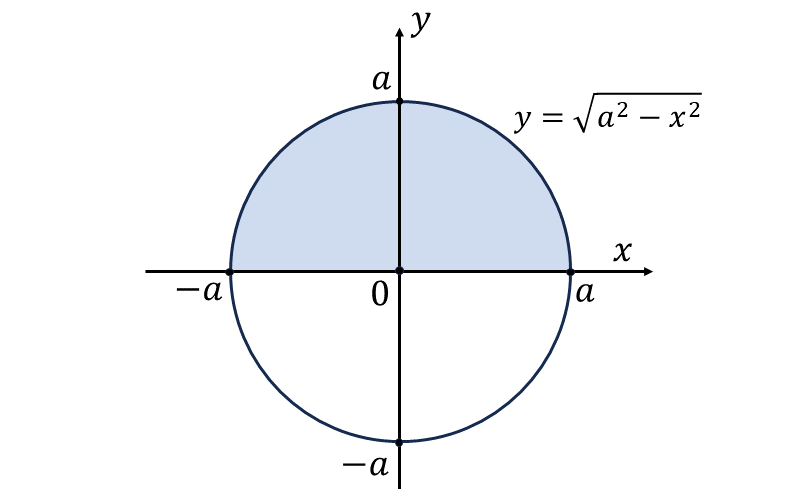
つまり、定積分 $\displaystyle\large{\int_{-a}^a \sqrt{a^2-x^2} \hspace{1pt} dx}$ は円の上半分の面積を表します。 $円の面積を積分で求める方法$

半径$\large{a\hspace{2pt}}$の円の面積は $\large{S=\pi a^2}$ であることから、問題の定積分は $$\large{\int_{-a}^a \sqrt{a^2-x^2} \hspace{1pt} dx = \frac{\pi}{2}a^2}$$ となります。

このように、半円を表す関数 $\displaystyle\large{y=\sqrt{a^2-x^2}}$ を含む積分では、円の面積から定積分が求められないかを考えることが定石です。

【1-1】円の面積を求める積分の計算

前章は関数を図示することで積分の計算を省略しましたが、本章では別解として積分による計算方法を示します。

まず、問題の定積分は偶関数であることから、 $$\large{ \int_{-a}^a \sqrt{a^2-x^2} \hspace{1pt} dx = 2\int_{0}^a \sqrt{a^2-x^2} \hspace{1pt} dx}$$ と変形します。

問題の定積分を計算するには、積分の変数$\large{x}$ を別の変数に置き換える置換積分法を使用します。

ここでは、$\large{x= a \sin t}$ とおいて積分を計算します。
変数$\large{x}$ の区間$\large{\hspace{1pt}[\hspace{1pt}0\hspace{1pt},\hspace{2pt}a\hspace{1pt}]}$ に対応する変数$\large{t}$ の区間を求めると、以下のようになります。

$\large{x}$	$\large{0 \to a}$
$\large{t}$	$\displaystyle\large{0 \to \frac{\pi}{2}}$

ここで、$\large{x= a\sin t}$ の両辺を $\large{t}$ で微分すると、三角関数の微分公式から $$\large{\frac{dx}{dt} = a\cos t}$$ となります。

よって、$\displaystyle\large{dx = a \cos t \hspace{1pt} dt}$ と表せます。

したがって、問題の定積分は以下のように計算されます。

\begin{eqnarray} \large \hspace{10pt}2\int_0^a \sqrt{a^2-x^2} \hspace{1pt} dx &\large =&\large 2\int_0^{\frac{\pi}{2}} \sqrt{a^2-a^2 \sin^2 t} \hspace{1pt}(a\cos t )\hspace{1pt} dt \hspace{10pt}\\[0.5em] \large &\large =&\large 2 a^2\int_0^{\frac{\pi}{2}} \sqrt{1- \sin^2 t} \cos t \hspace{1pt} dt\\[0.5em] \large &\large =&\large 2 a^2\int_0^{\frac{\pi}{2}} \cos^2 t \hspace{1pt} dt\\[0.5em] \end{eqnarray}

ここで、半角の公式 $$\large{\cos^2 t = \frac{1+\cos 2t}{2}}$$ から式変形すると、

\begin{eqnarray} \large \hspace{10pt}2 a^2\int_0^{\frac{\pi}{2}} \cos^2 t \hspace{1pt} dt &\large =&\large 2 a^2\int_0^{\frac{\pi}{2}} \frac{1+ \cos 2t}{2} \hspace{1pt} dt \\[0.5em] \large &\large =&\large a^2[\hspace{2pt}t + \frac{1}{2}\sin 2t\hspace{2pt}]_0^{\frac{\pi}{2}}\\[0.5em] \large &\large =&\large a^2\left(\hspace{1pt}\frac{\pi}{2}-0\right) +\frac{a^2}{2} (\sin \pi - \sin 0)\hspace{10pt}\\[0.5em] \large &\large =&\large \frac{\pi}{2}a^2\\[0.5em] \end{eqnarray}

したがって、 $$\large{\int_{-a}^a \sqrt{a^2-x^2} \hspace{1pt} dx = \frac{\pi}{2}a^2}$$ と求めることができます。

【2】問題と解き方

本章では、円の面積の積分に関連した問題について解説します。

問題(1)

以下の定積分を求めよ。
\begin{eqnarray} &&\large\int_{-\frac{1}{2}}^\frac{1}{2} \sqrt{1 -x^2} \hspace{1pt}\hspace{1pt} dx\\[0.7em] \end{eqnarray}

問題(2)

以下の定積分を求めよ。
\begin{eqnarray} &&\large\int_{0}^{2} \sqrt{-x^2 +2x} \hspace{1pt}\hspace{1pt} dx\\[0.7em] \end{eqnarray}

(解答と解説 : 問題(1) 問題(2) )

問題(1) 円の一部の面積を求める積分

【問題(1)】

次の定積分を求めよ。
\begin{eqnarray} &&\large\int_{-\frac{1}{2}}^\frac{1}{2} \sqrt{1 -x^2} \hspace{1pt}\hspace{1pt} dx\\[0.7em] \end{eqnarray}

【解答と解説】
関数 $\large{y=\sqrt{1-x^2} }$ の両辺を二乗すると、 $$\large{y^2 = 1-x^2}$$ すなわち、 $$\large{x^2 + y^2 = 1}$$ と変形されることから、関数 $\large{y=\sqrt{1-x^2} }$ は半径$\large{1\hspace{2pt}}$の円の上半分 ($\large{y \geqq 0}$) を表します。

先述したように、円を表す関数の積分の問題は、円の面積から定積分が求められないかを考えます。

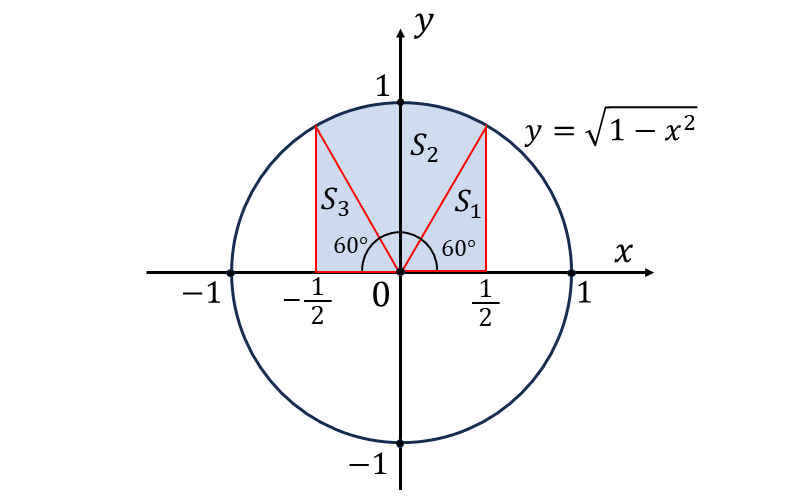
本問の定積分は、下の図の青色で示した半径$\large{1\hspace{1pt}}$の半円の $\displaystyle\large{-\frac{1}{2} \leqq x \leqq \frac{1}{2}}$ の範囲の面積を表します。 $円の面積を積分で求める方法$

ここで、上図の面積を三角形$\large{S_1,\hspace{1pt}S_3}$ と扇形$\large{S_2}$ の部分に分けて考えます。

まず、面積$\large{S_1\hspace{2pt}}$と$\large{\hspace{2pt}S_3}$ は底辺$\displaystyle\large{\hspace{2pt}\frac{1}{2}}$、高さ$\displaystyle\large{\hspace{2pt}\frac{\sqrt{3}}{2}}$ の三角形の面積のため、 \begin{eqnarray} \large S_1 = S_3 &\large =&\large \frac{1}{2}\times \frac{1}{2} \times \frac{\sqrt{3}}{2} \\[0.5em] \large &\large =&\large \frac{\sqrt{3}}{8} \\ \end{eqnarray} となります。

次に、面積$\large{\hspace{1pt}S_2\hspace{2pt}}$ は半径$\large{1\hspace{1pt}}$, 角度$\large{60°}$ の扇形の面積のため、 $$\large{S_2 = \pi \times 1^2 \times \frac{60}{360} = \frac{\pi}{6}}$$ となります。

したがって、求める定積分の値は \begin{eqnarray} \large \int_{-\frac{1}{2}}^\frac{1}{2} \sqrt{1 -x^2} \hspace{1pt}\hspace{1pt} dx&\large =&\large S_1 + S_2 + S_3\\[0.5em] \large &\large =&\large \frac{\pi}{6} + \frac{\sqrt{3}}{4} \\ \end{eqnarray} と求められます。

【別解と解説】
もしくは、置換積分法を利用した積分から解くこともできます。

まず、問題の定積分は偶関数であることから、 $$\large{ \int_{-\frac{1}{2}}^{\frac{1}{2}} \sqrt{1-x^2} \hspace{1pt} dx = 2\int_{0}^\frac{1}{2} \sqrt{1-x^2} \hspace{1pt} dx}$$ と変形します。

$\large{x= \sin t}$ とおき、変数$\large{x}$ の区間$\large{\hspace{1pt}[\hspace{1pt}0\hspace{1pt},\hspace{2pt}\frac{1}{2}\hspace{1pt}]}$ に対応する変数$\large{t}$ の区間を求めます。

$\large{x}$	$\displaystyle\large{0 \to \frac{1}{2}}$
$\large{t}$	$\displaystyle\large{0 \to \frac{\pi}{6}}$

ここで、$\large{x= \sin t}$ の両辺を $\large{t}$ で微分すると、三角関数の微分公式から $$\large{\frac{dx}{dt} = \cos t}$$ となります。

すなわち、$\displaystyle\large{dx = \cos t \hspace{1pt} dt}$ と表せます。

したがって、問題の定積分は以下のように計算されます。

\begin{eqnarray} \large \hspace{10pt}2\int_0^\frac{1}{2} \sqrt{1-x^2} \hspace{1pt} dx &\large =&\large 2\int_0^{\frac{\pi}{6}} \sqrt{1- \sin^2 t} \hspace{1pt}\cos t \hspace{1pt} dt\hspace{10pt} \\[0.5em] \large &\large =&\large 2 \int_0^{\frac{\pi}{6}} \cos^2 t \hspace{1pt} dt\\[0.5em] \end{eqnarray}

ここで、半角の公式 $$\large{\cos^2 t = \frac{1+\cos 2t}{2}}$$ から式変形すると、

\begin{eqnarray} \large \hspace{10pt}2 \int_0^{\frac{\pi}{6}} \cos^2 t \hspace{1pt} dt &\large =&\large 2 \int_0^{\frac{\pi}{6}} \frac{1+ \cos 2t}{2} \hspace{1pt} dt \\[0.5em] \large &\large =&\large [\hspace{2pt}t + \frac{1}{2}\sin 2t\hspace{2pt}]_0^{\frac{\pi}{6}}\\[0.5em] \large &\large =&\large \left(\hspace{1pt}\frac{\pi}{6}-0\right) +\frac{1}{2} \left(\sin \frac{\pi}{3} - \sin 0 \right)\hspace{10pt}\\[0.5em] \large &\large =&\large \frac{\pi}{6} + \frac{\sqrt{3}}{4}\\[0.5em] \end{eqnarray}

したがって、 $$\large{\int_{-\frac{1}{2}}^\frac{1}{2} \sqrt{1-x^2} \hspace{1pt} dx = \frac{\pi}{6} + \frac{\sqrt{3}}{4}}$$ と求めることができます。

問題(2) 平行移動した円の面積の積分

問題(2)

以下の定積分を求めよ。
\begin{eqnarray} &&\large\int_{0}^{2} \sqrt{-x^2 +2x} \hspace{1pt}\hspace{1pt} dx\\[0.7em] \end{eqnarray}

【解答と解説】
本問の定積分は、一見すると円の方程式とは異なるように見えますが、ルートの中の二次関数を平方完成をすると平行移動した円の方程式であることが分かります。

関数 $\large{y=\sqrt{-x^2 +2x}}$ の両辺を二乗し、平方完成すると以下のようになります。 \begin{eqnarray} \large y^2&\large =&\large -x^2 +2x\\[0.7em] \large &\large =&\large -(x^2 -2x) \\[0.7em] \large &\large =&\large -(x^2 -2x + 1) + 1 \\[0.7em] \large &\large =&\large -(x-1)^2 + 1 \\ \end{eqnarray}

すなわち、 $$\large{(x-1)^2 + y^2 = 1}$$ となります。

したがって、半径が$\large{\hspace{1pt}1\hspace{1pt}}$、中心が $\large{(\hspace{1pt}1\hspace{1pt},\hspace{2pt}0\hspace{1pt})}$ の円の上半分 $\large{(\mathrm{y \geqq 0})}$ を表す関数となります。

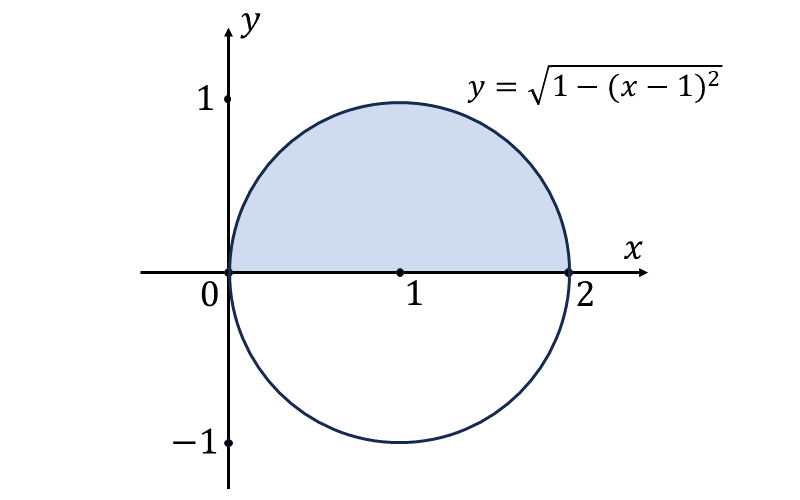
よって、問題の定積分 $\displaystyle\large{\int_{0}^{2} \sqrt{-x^2 +2x} \hspace{1pt}\hspace{1pt} dx}$ の表す領域を図示すると、以下の青色で示す範囲となります。 $平行移動した円の面積の積分$

したがって、問題の定積分は $$\large{\int_{0}^{2} \sqrt{-x^2 +2x} \hspace{1pt}\hspace{1pt} dx = \frac{\pi}{2}}$$ となります。

【別解と解説】
積分の計算から求める場合も、まず前記のようにルートの中を平方完成します。 $$\large{\int_{0}^{2} \sqrt{-x^2 +2x} \hspace{1pt}\hspace{1pt} dx = \int_{0}^{2} \sqrt{1-(x-1)^2 } \hspace{1pt}\hspace{1pt} dx\\[0.5em]}$$ 上式を置換積分法により変数を置き換えて積分を求めます。

中心が原点の円の積分 $\displaystyle\large{\int_{-1}^{1} \sqrt{1-x^2} \hspace{1pt}\hspace{1pt} dx}$ では $\large{x = \sin t}$ と置き換え積分することから類推し、$\large{x-1 = \sin t}$ とおいて積分します。

変数$\large{x}$ の区間$\large{\hspace{1pt}[\hspace{1pt}0\hspace{1pt},\hspace{2pt}2\hspace{1pt}]}$ に対応する変数$\large{t}$ の区間を求めます。

$\large{x}$	$\displaystyle\large{0 \to 2}$
$\large{t}$	$\displaystyle\large{-\frac{\pi}{2} \to \frac{\pi}{2}}$

ここで、$\large{x= \sin t}$ の両辺を $\large{t}$ で微分すると、三角関数の微分公式から $$\large{\frac{dx}{dt} = \cos t}$$ となります。

すなわち、$\displaystyle\large{dx = \cos t \hspace{1pt} dt}$ と表せます。

したがって、問題の定積分は以下のように計算されます。

\begin{eqnarray} \large \hspace{10pt}\int_{0}^{2} \sqrt{1-(x-1)^2 } \hspace{1pt}\hspace{1pt} dx &\large =&\large \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \sqrt{1- \sin^2 t} \hspace{1pt}\cos t \hspace{1pt} dt\hspace{10pt} \\[0.5em] \large &\large =&\large \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \cos^2 t \hspace{1pt} dt\\[0.5em] \end{eqnarray}

ここで、半角の公式 $$\large{\cos^2 t = \frac{1+\cos 2t}{2}}$$ から式変形すると、

\begin{eqnarray} \large \hspace{10pt}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \cos^2 t \hspace{1pt} dt &\large =&\large \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{1+ \cos 2t}{2} \hspace{1pt} dt \\[0.5em] \large &\large =&\large\frac{1}{2} [\hspace{2pt}t + \frac{1}{2}\sin 2t\hspace{2pt}]_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\\[0.5em] \large &\large =&\large \frac{1}{2}\left(\hspace{1pt}\frac{\pi}{2}+\frac{\pi}{2}\right) +\frac{1}{4} \left(\sin \pi - \sin (-\pi) \right)\hspace{10pt}\\[0.5em] \large &\large =&\large \frac{\pi}{2}\\[0.5em] \end{eqnarray}

したがって、 $$\large{\int_{0}^2 \sqrt{-x^2+2x} \hspace{1pt} dx = \frac{\pi}{2} }$$ と求めることができます。

トップページ > 数学基礎 > 極限・微積分 > 円の面積の積分

infomation

光学索引

あ行か行さ行た行な行は行ま行や行ら行わ行

\(\large{x}\)	\(\large{0 \to a}\)
\(\large{t}\)	\(\displaystyle\large{0 \to \frac{\pi}{2}}\)

\(\large{x}\)	\(\displaystyle\large{0 \to \frac{1}{2}}\)
\(\large{t}\)	\(\displaystyle\large{0 \to \frac{\pi}{6}}\)

\(\large{x}\)	\(\displaystyle\large{0 \to 2}\)
\(\large{t}\)	\(\displaystyle\large{-\frac{\pi}{2} \to \frac{\pi}{2}}\)