1/3公式 | 二次関数と接線に囲まれた面積
本項では、『1/3公式の使い方や導出』 と 『問題の解き方』について解説します。
【1】1/3公式とは
1/3公式 とは、以下のような 二次関数 \(\large{y=ax^2+bx+c}\) と 接線に囲まれる面積に成り立つ公式です。
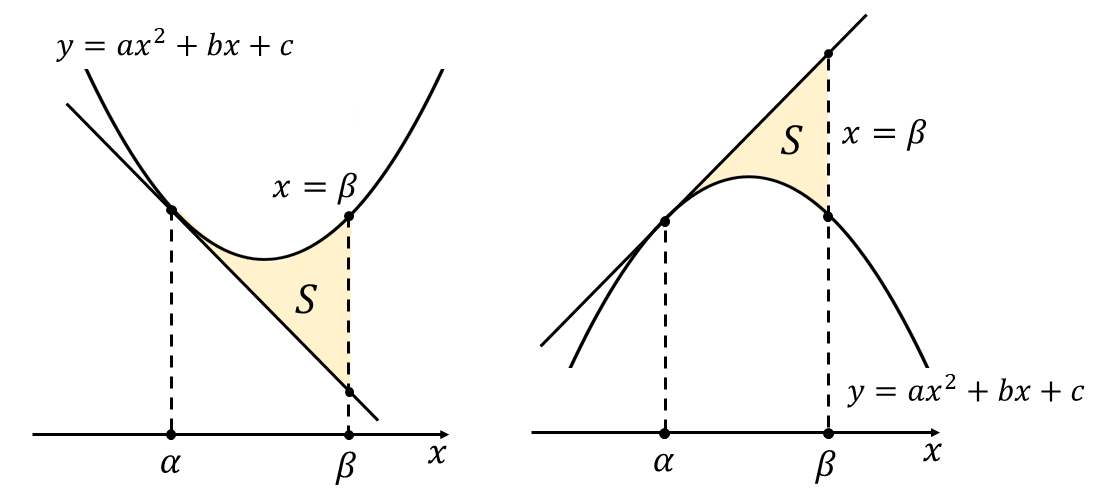
・曲線上の\(\large{\boldsymbol{\hspace{2pt}x=\alpha}}\) における接線
・直線\(\large{\boldsymbol{\hspace{2pt}x=\beta}\hspace{2pt}}\)
により 囲まれる面積\(\large{\hspace{1pt}S\hspace{2pt}}\)は以下のように求められる
$$\large{\displaystyle\large{S = \frac{|a|}{3}(\beta-\alpha)^3}}$$
1/3公式 を覚えておくと、『二次関数と接線, 直線に囲まれた面積』を瞬時に計算することができます。
・例題
\(\large{C}\) 上の点\(\large{(\hspace{1pt}-1\hspace{1pt},\hspace{1pt}10\hspace{1pt})}\) における接線, 曲線 \(\large{C}\), 直線\(\large{\hspace{1pt}x=2\hspace{2pt}}\)によって囲まれる面積 \(\large{S}\) を求めよ
【解答と解説】
曲線 \(\large{\hspace{2pt}y=2x^2-3x+5}\) 上の点\(\large{(\hspace{1pt}-1\hspace{1pt},\hspace{1pt}10\hspace{1pt})}\) における接線 と 曲線 \(\large{C}\)、直線\(\large{\hspace{1pt}x=2\hspace{2pt}}\)によって囲まれる面積 \(\large{S}\) を図示すると、以下のようになります。
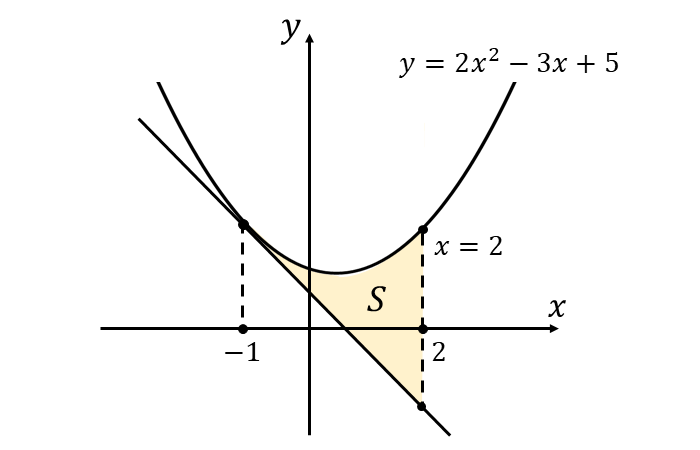
先述した1/3公式 $$\large{S = \frac{|a|}{3}(\beta-\alpha)^3}$$ において、二次関数の二次の係数が \(\large{a=2}\)、接点の\(\large{x\hspace{1pt}}\)座標が \(\large{\alpha=-1}\) 、\(\large{\hspace{1pt}\beta=2}\) であることから面積は \begin{eqnarray} \large S &\large =&\large \frac{|2|}{3}(2-(-1))^3 \\[0.5em] \large &\large =&\large 18 \\ \end{eqnarray} と求められます。
【別解と解説】
ここで、1/3公式を使わずに面積を求めてみます。
まず、曲線\(\large{C}\) 上の点\(\large{(\hspace{1pt}-1\hspace{1pt},\hspace{1pt}10\hspace{1pt})}\) における接線の方程式を求めます。
\(\large{f(x)=2x^2-3x+5}\) とすると、\(\large{f'(x)=4x-3}\) となります。
つまり、点\(\large(-1,10)\) における接線の傾きは \(\large{f'(-1)=-7}\) となります。
したがって、接線の方程式の公式 $$\large{y=f'(a)(x-a)+f(a)}$$ から、求める接線の方程式は \begin{eqnarray} \large y &\large =&\large -7(x-(-1)) +10 \\[0.5em] \large &\large =&\large -7x+3\\ \end{eqnarray} と求められます。
\(\large{-1 \leqq x \leqq 2}\) において、\(\large{2x^2-3x+5 \geqq -7x+3}\) であることから、面積\(\large{\hspace{1pt}S\hspace{2pt}}\) は以下のように求められます。
・1/3公式の証明
二次関数 \(\large{f(x)=ax^2+bx+c}\) と \(\large{x=\alpha\hspace{3pt}}\)における接線、直線\(\large{\hspace{1pt}x=\beta}\) に囲まれる面積\(\large{\hspace{1pt}S\hspace{2pt}}\)が
$$\displaystyle\large{S = \frac{|a|}{3}(\beta-\alpha)^3}$$
となることを証明します。
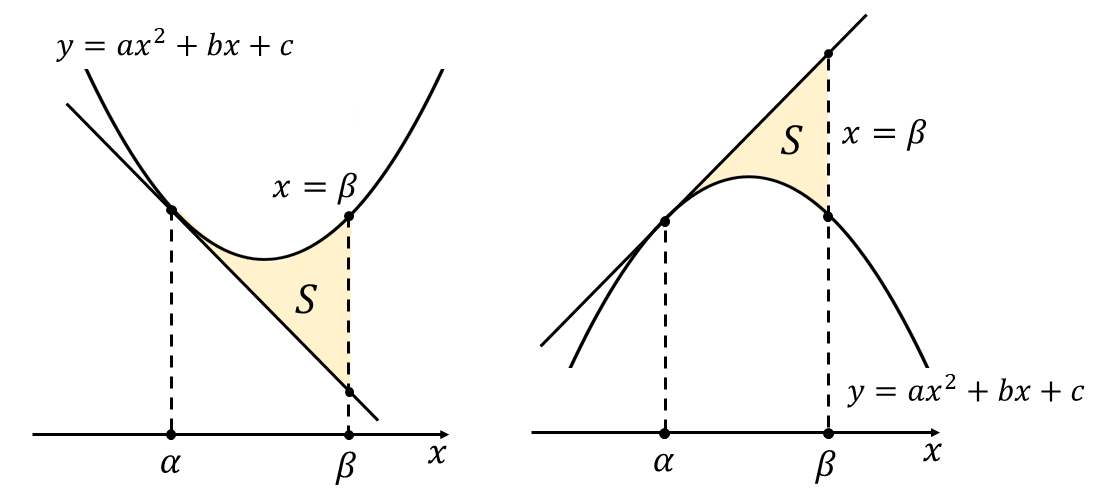
まず \(\large{f(x)=ax^2+bx+c}\) の 点(\(\large{\hspace{1pt}\alpha},\hspace{2pt}f(\alpha)\hspace{1pt}\)) における接線の方程式を求めます。
\(\large{f(x)=ax^2+bx+c}\) の導関数は \(\large{f'(x)=2ax+b}\) となります。
つまり、点(\(\large{\hspace{1pt}\alpha},\hspace{2pt}f(\alpha)\hspace{1pt}\)) における接線の傾きは \(\large{f'(\alpha)=2a\alpha+b}\) となります。
したがって、接線の方程式の公式 $$\large{y=f'(a)(x-a)+f(a)}$$ から、点(\(\large{\hspace{1pt}\alpha},\hspace{2pt}f(\alpha)\hspace{1pt}\)) で接する接線 は \begin{eqnarray} \large y &\large =& \large (2a\alpha+b)(x-\alpha) + a\alpha^2+b\hspace{1pt}\alpha + c\\[0.5em] &\large =&\large (2a\alpha+b)x -a\alpha^2+c \\[0.5em] \end{eqnarray} となります。
よって、(二次関数)-(接線の方程式) の絶対値の積分から 面積\(\large{\hspace{1pt}S\hspace{2pt}}\) を求めると、以下のようになります。
ここで、\(\large{(x-\alpha)^2 \geqq 0\hspace{1pt}}\) であるため、 $$\large{|(x-\alpha)^2| = (x-\alpha)^2}$$ となります。
したがって、
以上から $$\displaystyle\large{S = \frac{|a|}{3}(\beta-\alpha)^3}$$ が成り立ちます。
・証明の補足
証明の途中計算で以下の不定積分の式を使用しました。 $$\large{\int (x-\alpha)^2\hspace{1pt}dx = \frac{1}{3}(x-\alpha)^3+C}$$
上式は、二次関数の積分でよく表れるため、覚えておくと便利です。
置換積分法を用いて上式を導きます。
まず \(\large{x-\alpha =t }\) とおき、 \(\large{x =t+\alpha }\) の両辺を \(\large{t}\) で微分すると
$$\large{\frac{dx}{dt} = 1}$$
となります。すなわち、\(\large{dx = dt}\) と表せます。
したがって、 \begin{eqnarray} \large \int (x-\alpha)^2\hspace{1pt}dx &\large =&\large \int t^2\hspace{1pt}dt \\[0.5em] \large &\large =&\large \frac{1}{3}t^3 +C\\[0.5em] \large &\large =&\large \frac{1}{3}(x-\alpha)^3 +C\\[0.5em] \end{eqnarray} となり、以下の不定積分が成り立ちます。 $$\large{\int (x-\alpha)^2\hspace{1pt}dx = \frac{1}{3}(x-\alpha)^3+C}$$
【2】1/3公式 | 接する2つの二次関数と直線
1/3公式の応用として、以下のような \(\large{\hspace{1pt}2\hspace{2pt}}\)つの二次関数 と 直線 \(\large{x=\beta}\) に囲まれる面積についても 瞬時に計算する公式があります。
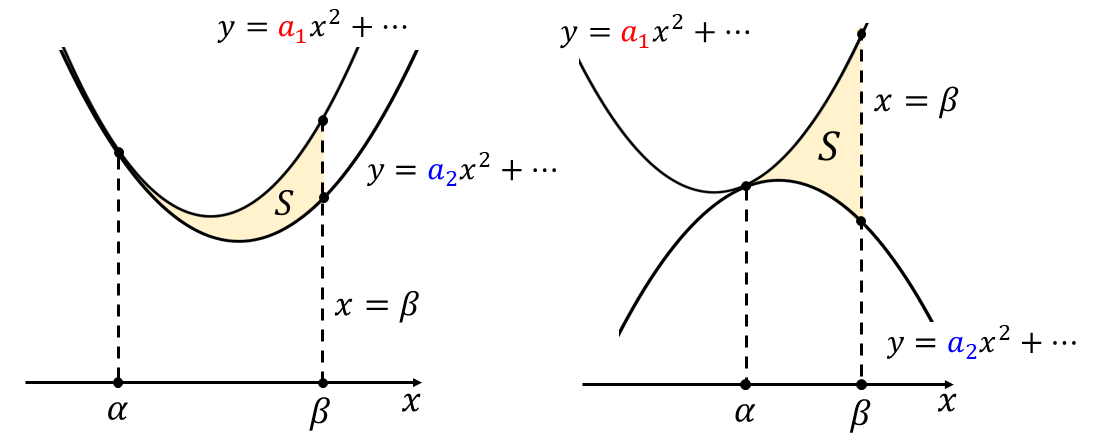
・曲線2 : \(\large{\boldsymbol{y=a_2x^2+b_2x+c_2\hspace{2pt}}}\)
・直線 : \(\large{\boldsymbol{\hspace{2pt}x=\beta}\hspace{2pt}}\)
により 囲まれる面積\(\large{\hspace{1pt}S\hspace{2pt}}\)は以下のように求められる
$$\large{\displaystyle\large{S = \frac{|a_1-a_2|}{3}(\beta-\alpha)^3}}$$
・例題
曲線\(\large{C_1, C_2}\) と 直線\(\large{\hspace{1pt}x=2\hspace{3pt}}\)によって囲まれる面積 \(\large{S}\) を求めよ
【解答と解説】
曲線\(\large{C_1}\) : \(\large{\hspace{2pt}y=2x^2}\) と 曲線\(\large{C_2}\) : \(\large{\hspace{2pt}y=3x^2+2x+1}\) の式から \(\large{y}\) を削除すると
\begin{eqnarray}
\large
3x^2+2x+1 &\large =&\large 2 x^2 \\[0.5em]
\large
x^2 + 2x + 1&\large =&\large 0 \\[0.5em]
\large
(x+1)^2&\large =&\large 0 \\
\end{eqnarray}
すなわち、\(\large{x=-1}\) で重解を持つことから、曲線\(\large{C_1, C_2}\) は \(\large{x=-1}\) で接することが分かります。
求める曲線\(\large{C_1, C_2}\) と 直線\(\large{\hspace{1pt}x=2\hspace{2pt}}\)によって囲まれる面積 \(\large{S}\) を図示すると、以下のようになります。
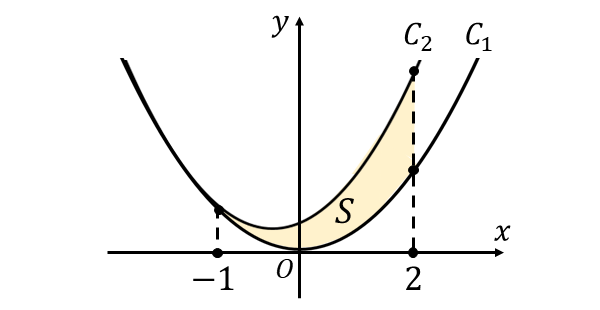
接する\(\large{\hspace{2pt}2\hspace{1pt}}\)つの二次関数の1/3公式 $$\large{S = \frac{|a_1-a_2|}{3}(\beta-\alpha)^3}$$ において、二次関数の二次の係数が \(\large{a_1=2\hspace{2pt}}\), \(\large{a_2=3}\), 接点の\(\large{x\hspace{1pt}}\)座標が \(\large{\alpha=-1}\), 直線の式の\(\large{x\hspace{1pt}}\)座標が \(\large{\hspace{1pt}\beta=2}\) であることから面積は \begin{eqnarray} \large S &\large =&\large \frac{|2-3|}{3}(2-(-1))^3 \\[0.5em] \large &\large =&\large 9 \\ \end{eqnarray} と求められます。
【別解と解説】
ここで、1/3公式を使わずに面積を求めてみます。
\(\large{-1 \leqq x \leqq 2}\) において、\(\large{3x^2+2x+1 \geqq 2x^2}\) であることから、面積\(\large{\hspace{1pt}S\hspace{2pt}}\)は以下のようになります。
・1/3公式の証明 | 接する2つの二次関数と直線
曲線\(\large{C_1}\) : \(\large{\hspace{2pt}f(x)=a_1x^2+b_1x+c_1}\) と 曲線\(\large{C_2}\) : \(\large{\hspace{2pt}g(x)=a_2x^2+b_2x+c_2}\) が \(\large{x=\alpha\hspace{1pt}}\) で接点を持つとき、\(\large{2\hspace{1pt}}\)つの曲線 と 直線\(\large{\hspace{1pt}x=\beta}\) に囲まれる面積\(\large{\hspace{1pt}S\hspace{2pt}}\)が
$$\displaystyle\large{S = \frac{|a_1-a_2|}{3}(\beta-\alpha)^3}$$
となることを証明します。

\(\large{f(x)}\) と \(\large{g(x)}\) が \(\large{x=\alpha}\) で接点を持つとき、\(\large{f(x)-g(x)=0}\) が \(\large{x=\alpha}\) の重解を持つため、 $$\large{f(x)-g(x)=(a_1-a_2)(x-\alpha)^2}$$ と表せます。
ここで、二次関数 \(\large{f(x)\hspace{1pt},\hspace{2pt}g(x)}\) と 直線 \(\large{x=\beta}\) で囲まれる面積\(\large{\hspace{1pt}S\hspace{2pt}}\)は、以下のように表せます。 \begin{eqnarray} \large S &\large =& \large \int_\alpha^\beta |f(x)-g(x)|\hspace{1pt}dx \\[0.5em] \large &\large =&\large \int_\alpha^\beta |(a_1-a_2)(x-\alpha)^2| \hspace{1pt}dx \\[0.5em] \large &\large =&\large |a_1-a_2|\int_\alpha^\beta |(x-\alpha)^2| \hspace{1pt}dx \\[0.5em] \end{eqnarray} ここで、\(\large{(x-\alpha)^2 \geqq 0\hspace{1pt}}\) であるため、 $$\large{|(x-\alpha)^2| = (x-\alpha)^2}$$ となります。
したがって、
以上から $$\displaystyle\large{S = \frac{|a_1-a_2|}{3}(\beta-\alpha)^3}$$ が成り立ちます。
【3】問題と解き方
本章では、1/3公式 に関連した問題について解説します。
曲線 \(\large{C}\) と \(\large{x\hspace{1pt}}\)軸 , \(\large{y\hspace{1pt}}\)軸 によって囲まれる面積 \(\large{S}\) を求めよ
曲線\(\large{C_1, C_2}\) と 直線\(\large{\hspace{1pt}x=2\hspace{3pt}}\)によって囲まれる面積 \(\large{S}\) を求めよ
問題(1) | 二次関数とx軸,y軸に囲まれた面積
曲線 \(\large{C}\) と \(\large{x\hspace{1pt}}\)軸 , \(\large{y\hspace{1pt}}\)軸 によって囲まれる面積 \(\large{S}\) を求めよ
【解答と解説】
二次関数 \(\large{y=(x-3)^2}\) と \(\large{x\hspace{1pt}}\)軸 , \(\large{y\hspace{1pt}}\)軸 に囲まれた面積を図示すると、以下のようになります。
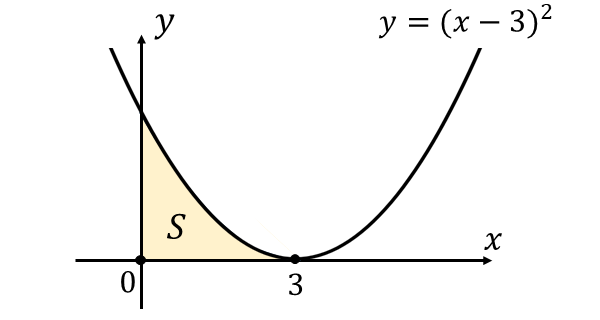
1/3公式から面積\(\large{\hspace{1pt}S\hspace{2pt}}\)は \begin{eqnarray} \large S &\large =&\large \frac{|a|}{3}(\beta-\alpha)^3\\[0.5em] \large &\large =&\large \frac{|1|}{3}(3-0)^3\\[0.5em] \large &\large =&\large 9\\[0.5em] \end{eqnarray} と求められます。
問題(2) | 2つの二次関数と直線に囲まれた面積
曲線\(\large{C_1, C_2}\) と 直線\(\large{\hspace{1pt}x=2\hspace{3pt}}\)によって囲まれる面積 \(\large{S}\) を求めよ
【解答と解説】
\(\large{\hspace{2pt}y=-2x^2+2}\) と \(\large{\hspace{2pt}y=x^2+6x + 5}\) の式から \(\large{y}\) を削除すると
\begin{eqnarray}
\large
x^2+6x + 5 &\large =&\large -2x^2+2 \\[0.5em]
\large
3x^2 + 6x + 3 &\large =&\large 0 \\[0.5em]
\large
3(x+1)^2&\large =&\large 0 \\
\end{eqnarray}
すなわち、\(\large{x=-1}\) で重解を持つことから、 曲線\(\large{C_1, C_2}\) は \(\large{x=-1}\) で接することが分かります。
求める曲線\(\large{C_1, C_2}\) と 直線\(\large{\hspace{1pt}x=2\hspace{2pt}}\)によって囲まれる面積 \(\large{S}\) を図示すると、以下のようになります。
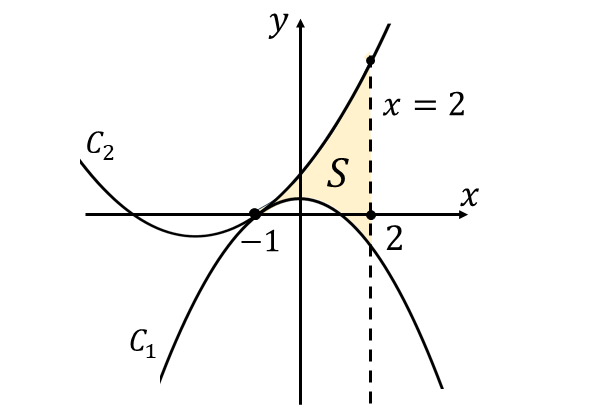
接する\(\large{\hspace{2pt}2\hspace{1pt}}\)つの二次関数の1/3公式 $$\large{S = \frac{|a_1-a_2|}{3}(\beta-\alpha)^3}$$ において、二次関数の二次の係数が \(\large{a_1=-2\hspace{2pt}}\), \(\large{a_2=1}\), 接点の\(\large{x\hspace{1pt}}\)座標が \(\large{\alpha=-1}\), 直線の式の\(\large{x\hspace{1pt}}\)座標が \(\large{\hspace{1pt}\beta=2}\) であることから面積は \begin{eqnarray} \large S &\large =&\large \frac{|-2-1|}{3}(2-(-1))^3 \\[0.5em] \large &\large =&\large 27 \\ \end{eqnarray} と求められます。