指数法則による計算

本項では、『指数法則による計算』、『指数が0や負,有理数のときの表記』、『指数法則の問題』について解説しています。

【1】指数法則

ある数 \(\large{a}\) を \(\large{n}\)回かけ合わせた数を 『\(\large{a}\)の\(\large{n}\)乗』といい、\(\large{a^n}\) と表記します。
例えば、\(\large{2}\) の \(\large{4}\)乗である \(\large{2^4}\) を式で表すと、以下のようになります。 $$\large{2^4 = 2 \times 2 \times 2 \times 2}$$

\(\large{a^n}\) を \(\large{a}\) の累乗といい、\(\large{a}\) を累乗の底、\(\large{n}\) を累乗の指数といいます。
例えば、\(\large{2^4}\) の底は \(\large{2}\)、指数は \(\large{4}\) となります。

【1-1】指数法則とは

指数法則とは、正の整数\(\large{n,m}\)に成り立つ、以下の式のことをいいます。

指数法則に具体的な値を入れると、以下のような計算が成り立つことが分かります。 \begin{eqnarray} \large 2^4 \times 2^3&\large =&\large 2^7\\ \large (2^4)^3&\large=&\large 2^{12}\\ \large \large (2\times5)^3&\large =&\large 2^3 \times 5^3\\ \end{eqnarray}

(指数が正の整数である場合の問題は後述しています。問題(1))

【1-2】指数が0の場合

上記の指数法則を、\(\large{0}\) や、負の数、有理数にまで拡張した場合の指数について考えます。

まず、指数が\(\large{0}\)である場合について考えます。
\(\large{2}\) の累乗は、\(\large{2^1=2}\)、\(\large{2^2=4}\)、\(\large{2^3=8}\) と指数が \(\large{1}\) 増えるごとに、\(\large{\times 2}\)倍されます。

逆に指数が \(\large{1}\) 減ると \(\large{2}\) で割ることになります。したがって、指数が \(\large{0}\) のときは、 \(\large{2^1=2}\)を \(\large{2}\) で割ることで \(\large{2^0=\color{red}{1}}\) と定めることができます。

また、\(\large{3}\) の累乗の場合でも \(\large{3^1=3}\)を \(\large{3}\) で割ることで \(\large{3^0=\color{red}{1}}\) と定めることができます。

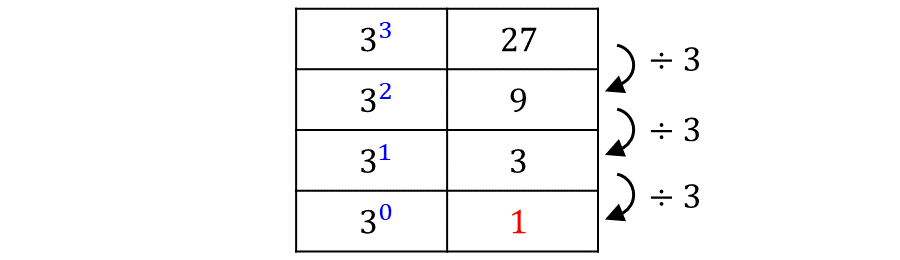
このように指数が \(\large{0}\) の場合は、底の値 \(\large{a}\) に関わらず\(\large{a^0 = 1}\) となります。

【1-3】指数が負の場合

指数が \(\large{0}\) の式 \(\large{a^0=1}\) から、さらに指数を減らすことで、指数が負の場合を考えることができます。 例えば、\(\large{a=2}\) のとき、\(\large{2^0=1}\) に対して指数を \(\large{1}\) だけ減らすとき、\(\large{2}\) で割ればよいので、\(\large{2^{-1}=\frac{1}{2}}\)となります。

同様に、\(\displaystyle \large{2^{-2}=\frac{1}{2^{2}}}\)、\(\displaystyle \large{2^{-3}=\frac{1}{2^{3}}}\)となります。

このように、指数が負である場合は、\(\displaystyle \large{a^{-n} = \frac{1}{a^n}}\) とすることができます。

指数が \(\large{0}\) と負の整数であるについてまとめると、以下のようになります。

上記のように0と負の整数の指数を定めることで、任意の整数\(\large{m,n}\)について指数法則が成り立ちます。

ここで、\(\large{a^m \div a^{n}}\)を計算すると、指数が負の整数である場合より $$\large{a^m \div a^{n} = a^m \times \frac{1}{a^n} =a^m \times a^{-n} = a^{m-n}}$$ とすることができます。
この式変形は、指数法則を用いた計算でよく使用されます。

(指数が0や負の整数である場合の問題は後述しています。問題(2))

【1-4】指数が有理数の場合

次に指数が有理数である場合について考えます。

指数法則の \(\large{(a^m)^n = a^{mn}}\) の式に対して、\(\large{a=3}\)、\(\large{m=\frac{1}{2}}\)、\(\large{n=2}\)の場合を考えると、 $$\large{(3^{\frac{1}{2}})^2 = 3^{1}=3}$$ すなわち、二乗すると \(\large{3}\) になる数が\(\large{3^{\frac{1}{2}}}\)であることが分かります。 したがって、\(\large{\frac{1}{2}}\)を指数にもつ \(\large{3^{\frac{1}{2}}}\) は、\(\large{3}\) の平方根となります。 $$\large{3^{\frac{1}{2}} = \sqrt{3}}$$

同様に、\(\large{\frac{1}{3}}\)は三乗根、\(\large{\frac{1}{4}}\)は四乗根を表します。 $$\large{2^{\frac{1}{3}}=\sqrt[3]{2}}$$ $$\large{5^{\frac{1}{4}}=\sqrt[4]{5}}$$

一般的には、\(\large{a>0}\)、\(\large{n,m}\)を正の整数、\(\large{r}\)を正の有理数 とした累乗を以下のように定めます。

上記のように定めることで、指数法則が任意の有理数に対しても成り立ちます。

(指数が有理数である場合の問題は後述しています。問題(3)～(5))

【2】指数法則の問題

指数法則に関連した問題を解説します。

問題(1) 正の整数の指数

【解答と解説】
以下の指数法則から、適切な式を選び計算します。 $$\large{a^m \times a^n = a^{m+n}}$$ $$\large{a^m \div a^n = a^{m-n}}$$ $$\large{(a^m)^n = a^{mn}}$$ $$\large{(ab)^n = a^n b^n}$$

まず、\(\large{a^m \times a^n = a^{m+n}}\)を利用して式を変形します。 $$\large{2^3 \times 2^6 \div 2^7 = 2^9 \div 2^7}$$ 次に、\(\large{a^m \div a^n = a^{m-n}}\)を利用して式を変形します。 $$\large{2^9 \div 2^7 = 2^2}$$ したがって、 $$\large{2^3 \times 2^6 \div 2^7 = 4}$$

問題(2) 0や負の整数の指数

【解答と解説】
指数が \(\large{0}\) のときは底によらず \(\large{1}\) となるため、 $$\large{7^0=1}$$ となります。

また、以下のように底が \(\large{3}\) の指数 \(\large{3^n}\) の形にそろえます。 $$\large{1 \times3^{-1} \times 9^{-2}=3^{-1} \times (3^2)^{-2} }$$ 次に、以下の指数法則から、適切な式を選び計算します。 $$\large{a^m \times a^n = a^{m+n}}$$ $$\large{a^m \div a^n = a^{m-n}}$$ $$\large{(a^m)^n = a^{mn}}$$ $$\large{(ab)^n = a^n b^n}$$

\(\large{(a^m)^n = a^{mn}}\)を利用して式を変形すると、 $$\large{3^{-1} \times (3^2)^{-2} = 3^{-1} \times 3^{-4} }$$ また、\(\large{a^m \times a^n = a^{m+n}}\)を利用して式を変形すると、 $$\displaystyle \large{3^{-1} \times 3^{-4} =3^{-5} =\frac{1}{3^5}}$$ したがって、 $$\large{7^{0} \times3^{-1} \times 9^{-2} = \frac{1}{243}}$$

問題(3) 有理数の指数

【解答と解説】
まず、与えられた式を指数 \(\large{a^n}\) の形に変形します。 $$\large{{(81^{\frac{1}{6}})}^{\frac{3}{4}}={((3^4)^{\frac{1}{6}})}^{\frac{3}{4}}}$$

次に、以下の指数法則から、適切な式を選び計算します。 $$\large{a^m \times a^n = a^{m+n}}$$ $$\large{a^m \div a^n = a^{m-n}}$$ $$\large{(a^m)^n = a^{mn}}$$ $$\large{(ab)^n = a^n b^n}$$

ここでは、\(\large{(a^m)^n = a^{mn}}\) を利用して式を変形します。 $$\large{{((3^4)^{\frac{1}{6}})}^{\frac{3}{4}} = {(3^{\frac{4}{6}})}^{\frac{3}{4}}=3^{\frac{1}{2}}}$$ したがって、 $$\displaystyle \large{{(81^{\frac{1}{6}})}^{\frac{3}{4}} = \sqrt{3}}$$

問題(4) 有理数の指数

【解答と解説】
まず以下のように指数 \(\large{2^n}\) の形にそろえます。 $$\large{4^{\frac{3}{2}} \times64^{\frac{3}{8}} \div 32^{\frac{1}{4}} = (2^2)^{\frac{3}{2}} \times(2^6)^{\frac{3}{8}} \div (2^5)^{\frac{1}{4}} }$$

次に、以下の指数法則から、適切な式を選び計算します。 $$\large{a^m \times a^n = a^{m+n}}$$ $$\large{a^m \div a^n = a^{m-n}}$$ $$\large{(a^m)^n = a^{mn}}$$ $$\large{(ab)^n = a^n b^n}$$

ここでは、\(\large{(a^m)^n = a^{mn}}\) を利用して式を変形します。 $$\large{(2^2)^{\frac{3}{2}} \times(2^6)^{\frac{3}{8}} \div (2^5)^{\frac{1}{4}} = 2^3 \times 2^\frac{9}{4} \div 2^\frac{5}{4}}$$ 次に、\(\large{a^m \times a^n = a^{m+n}}\) と \(\large{a^m \div a^n = a^{m-n}}\) を利用して式を変形します。 $$\large{2^{3} \times 2^\frac{9}{4} \div 2^\frac{5}{4} = 2^4}$$ したがって、 $$\large{4^{\frac{3}{2}} \times64^{\frac{3}{8}} \div 32^{\frac{1}{4}} = 16}$$

問題(5) 有理数の指数

【解答と解説】
まず以下のように指数 \(\large{3^n}\) に変形します。 $$\large{\left(\frac{1}{9}\right)^{-\frac{5}{6}} \div \left(\frac{1}{27}\right)^{-\frac{2}{9}} = \left(\frac{1}{3^2}\right)^{-\frac{5}{6}} \div \left(\frac{1}{3^3}\right)^{-\frac{2}{9}}}$$

上式を負の指数 \(\displaystyle \large{\frac{1}{a^n} = a^{-n}}\) を使用して書き換えます。 $$\large{\left(\frac{1}{3^2}\right)^{-\frac{5}{6}} \div \left(\frac{1}{3^3}\right)^{-\frac{2}{9}} = (3^{-2})^{-\frac{5}{6}} \div (3^{-3})^{-\frac{2}{9}}}$$

ここで、指数法則 \(\large{(a^m)^n = a^{mn}}\) を利用して式を変形します。 $$\large{(3^{-2})^{-\frac{5}{6}} \div (3^{-3})^{-\frac{2}{9}} = 3^\frac{5}{3} \div 3^\frac{2}{3} }$$ 指数法則 \(\large{a^m \div a^n = a^{m-n}}\) から、 $$\large{3^\frac{5}{3} \div 3^\frac{2}{3} = 3}$$ したがって、 $$\large{\left(\frac{1}{9}\right)^{-\frac{5}{6}} \div \left(\frac{1}{27}\right)^{-\frac{2}{9}} = 3}$$

---