平均変化率と微分係数

本項では以下の内容を解説します。

• ・平均変化率
• ・微分係数
• ・問題と解き方

【1】平均変化率とは

ある関数 \(\large{y=f(x)}\) において \(\large{x}\) の値が \(\large{\hspace{1pt}a\hspace{1pt}}\) から \(\large{\hspace{1pt}b\hspace{1pt}}\) まで変化するとき、
  ・ \(\large{x}\) の変化量は \(\large{b-a}\)
  ・ \(\large{y}\) の変化量は \(\large{f(b)-f(a)}\)
と表されます。

ここで、\(\large{x}\) の変化量に対する \(\large{y}\) の変化量の割合は以下の式で計算されます。

上式で表される\(\large{x}\) の変化量に対する \(\large{y}\) の変化量を、関数\(\large{f(x)}\)の 平均変化率 といいます。

以下の図のように、平均変化率とは 関数\(\large{f(x)}\)上の 点\(\large{(\hspace{1pt}a\hspace{1pt},\hspace{1pt}f(a)\hspace{1pt})}\)、点\(\large{(\hspace{1pt}b\hspace{1pt},\hspace{1pt}f(b)\hspace{1pt})}\) の2点を通る直線の傾きを意味します。

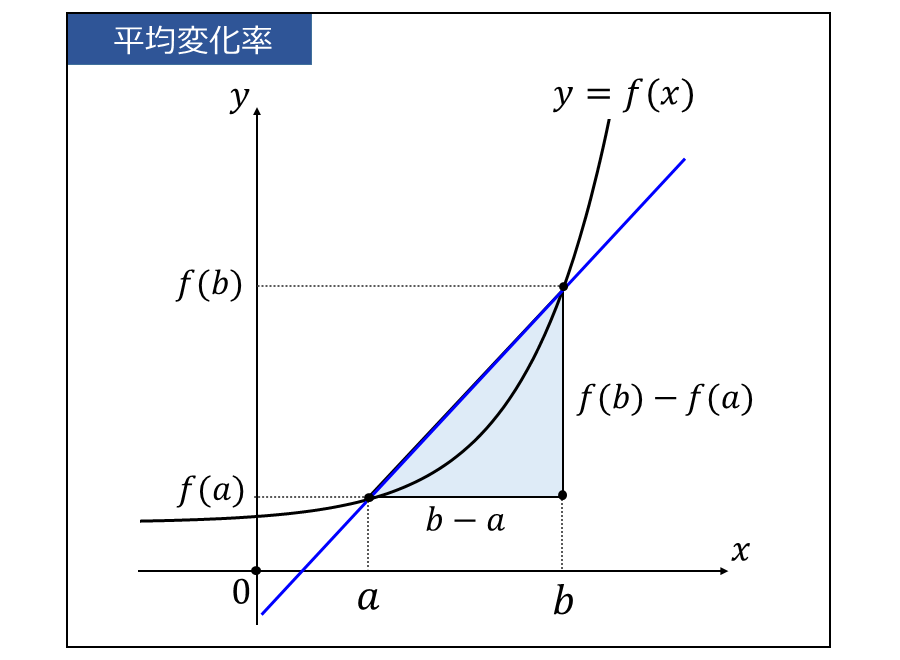
・計算例

平均変化率の式から、 $$\large{\frac{f(b)-f(a)}{b-a}=\frac{3^2-1^2}{3-1}=4}$$ となります。

したがって、関数 \(\displaystyle \large{f(x)=x^2}\) の \(\large{x=1}\) から \(\large{x=3}\) における平均変化率は \(\large{4}\) となります。

【2】微分係数とは

平均変化率の式 $$\large{\frac{f(b)-f(a)}{b-a}}$$ において、\(\large{x}\) の変化量 を \(\large{h=b-a}\) とおいて変形すると、以下のようになります。

・計算例

平均変化率の式から、 \begin{eqnarray} \large \frac{f(a+h)-f(a)}{h}&\large =&\large\frac{(2+h)^2-2^2}{h} \\[0.5em] \large &\large =&\large \frac{h^2+4h}{h} \\[0.5em] \large &\large =&\large 4+h \\ \end{eqnarray} と求められます。

したがって、関数 \(\displaystyle \large{f(x)=x^2}\) の \(\large{x=2}\) から \(\large{x=2+h}\) における平均変化率は \(\large{4+h}\) となります。

【2-1】極限値

上記の関数 \(\large{f(x)=x^2}\) の \(\large{x=2}\) から \(\large{x=2+h}\) までの平均変化率 $$\large{\frac{f(2+h)-f(2)}{h}=4+h}$$ において、\(\large{h}\) の値を限りなく \(\large{0}\) に近づけたときの値を $$\large{\lim_{h \to 0} (4+h)}$$ と記述します。

上式では、\(\large{4+h}\) の \(\large{h}\) を限りなく \(\large{0}\) に近づけると、\(\large{4}\) に限りなく近づき $$\large{\lim_{h \to 0} (4+h) = 4}$$ となります。

このとき、『\(\large{4}\) を \(\large{h}\) が限りなく \(\large{0}\) に近づいたときの \(\large{4+h}\) の極限値』といいます。

【2-2】微分係数

関数 \(\large{y=f(x)}\) において \(\large{x}\) の値が \(\large{\hspace{1pt}a\hspace{1pt}}\) から \(\large{\hspace{1pt}a+h\hspace{1pt}}\) における平均変化率は $$\large{\frac{f(a+h)-f(a)}{h}}$$ となります。

ここで、上式の \(\large{h}\) の値を限りなく \(\large{0}\) に近づけたときの値を微分係数といいます。

先述した関数 \(\large{f(x)=x^2}\) の \(\large{x=2}\) から \(\large{x=2+h}\) までの平均変化率の\(\large{h}\) を限りなく \(\large{0}\) に近づけたときの値は $$\large{\lim_{h \to 0}\frac{f(2+h)-f(2)}{h}=4}$$ となりました。

したがって、関数 \(\large{f(x)=x^2}\) の \(\large{x=2}\) における微分係数は \(\large{4}\) となります。

【2-3】微分係数の意味

ここで、下図に関数\(\large{f(x)}\)上の 点\(\large{P}\)\(\large{(\hspace{1pt}a\hspace{1pt},\hspace{1pt}f(a)\hspace{1pt})}\)、点\(\large{Q}\)\(\large{(\hspace{1pt}a+h\hspace{1pt},\hspace{1pt}f(a+h)\hspace{1pt})}\) の2点を通る直線を示します。

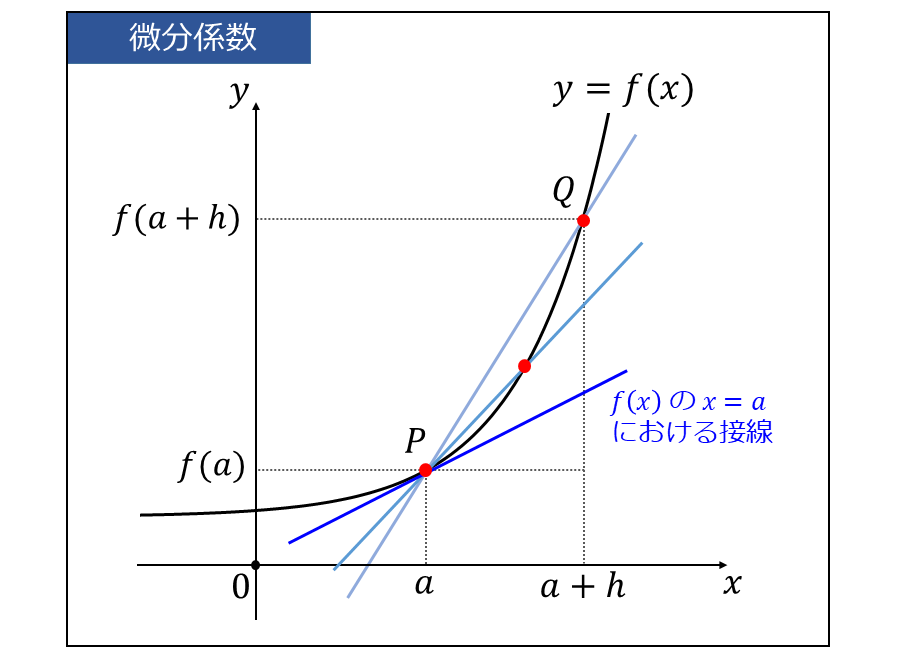
\(\large{h}\) が限りなく \(\large{0}\) に近づくとき、上図の 点\(\large{Q}\) が 点\(\large{P}\) に限りなく近づくことを表します。
点\(\large{Q}\) が 点\(\large{P}\) に限りなく近づくとき、直線\(\large{PQ}\) は 曲線\(\large{f(x)}\) の 点\(\large{P(x=a)}\) を通る接線となります。

微分係数\(\large{f'(a)}\) とは、下図のように曲線 \(\large{y=f(x)}\) の \(\large{x=a}\) における接線の傾きを意味します。

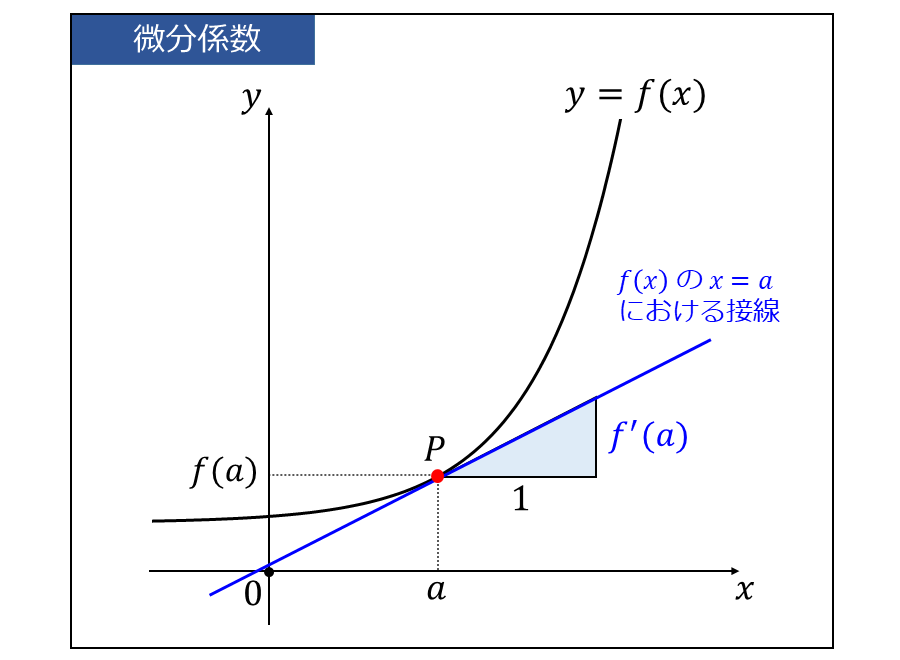
【3】問題と解き方

問題1 は、平均変化率を求める問題です。
(解答と解説 : 問題1)

問題2,問題3 は、微分係数を求める問題です。
(解答と解説 : 問題2 問題3)

問題4 は、平均変化率の結果から 変化率を計算した \(\large{x}\)の範囲を求める問題です。
(解答と解説 : 問題4)

問題5 は、2点を通る直線の傾きと、接線の傾きが一致するという条件から接点の座標を求める問題です。
(解答と解説 : 問題5)

問題.1 平均変化率の問題

【解答と解説】
関数\(\large{f(x)}\) の \(\large{x=a}\) から \(\large{x=b}\) における平均変化率の式 $$\large{\frac{f(b)-f(a)}{b-a}}$$ から \begin{eqnarray} \large \frac{f(3)-f(1)}{3-1}&\large =&\large\frac{(2\cdot 3^2+1)-(2\cdot 1^2+1)}{2} \\[0.5em] \large &\large =&\large \frac{19-3}{2} \\[0.5em] \large &\large =&\large 8 \\ \end{eqnarray} と求められます。

問題.2 微分係数の問題

【解答と解説】
関数\(\large{f(x)}\) の \(\large{x=a}\) における微分係数の式 $$\large{ f'(a) = \lim_{h \to 0}\frac{f(a+h)-f(a)}{h}}$$ から \begin{eqnarray} \large f'(a) &\large =&\large\lim_{h \to 0}\frac{(2+h)^3-2^3}{h} \\[0.5em] \large &\large =&\large \lim_{h \to 0}\frac{8+12 h + 6 h^2+h^3-8}{h} \\[0.5em] \large &\large =&\large \lim_{h \to 0}\frac{h^3+6h^2+12h}{h} \\[0.5em] \large &\large =&\large \lim_{h \to 0}(h^2 + 6h +12) \\[0.5em] \large &\large =&\large 12 \\[0.5em] \end{eqnarray} と求められます。

問題.3 微分係数の問題

【解答と解説】
関数\(\large{f(x)}\) の \(\large{x=a}\) における微分係数の式 $$\large{ f'(a) = \lim_{h \to 0}\frac{f(a+h)-f(a)}{h}}$$ から \begin{eqnarray} \large f'(a) &\large =&\large\lim_{h \to 0}\frac{\sqrt{2+h}-\sqrt{2}}{h} \\[0.5em] \large &\large =&\large \lim_{h \to 0}\frac{(\sqrt{2+h}-\sqrt{2})(\sqrt{2+h}+\sqrt{2})}{h(\sqrt{2+h}+\sqrt{2})} \\[0.5em] \large &\large =&\large \lim_{h \to 0}\frac{(\sqrt{2+h})^2-(\sqrt{2})^2}{h(\sqrt{2+h}+\sqrt{2})} \\[0.5em] \large &\large =&\large \lim_{h \to 0}\frac{h}{h(\sqrt{2+h}+\sqrt{2})} \\[0.5em] \large &\large =&\large \lim_{h \to 0}\frac{1}{\sqrt{2+h}+\sqrt{2}} \\[0.5em] \large &\large =&\large \frac{\sqrt{2}}{4} \\[0.5em] \end{eqnarray} と求められます。

問題.4 平均変化率から定数aの決定

本問は、平均変化率を求める範囲に 定数\(\large{a}\) が含まれている場合の問題です。

関数\(\large{f(x)=x^2}\) の \(\large{x=a}\) から \(\large{x=a+1}\) における平均変化率は、 \begin{eqnarray} \large \frac{f(a+1)-f(a)}{(a+1)-a}&\large =&\large\frac{ (a+1)^2-a^2}{1} \\[0.5em] \large &\large =&\large 2a+1 \\[0.5em] \end{eqnarray} となります。

求められた平均変化率が、\(\large{7}\) に等しくなるため、 \begin{eqnarray} \large 2a+1&\large =&\large7 \\[0.5em] \large a&\large =&\large 3 \\[0.5em] \end{eqnarray} したがって、定数\(\large{a}\) の値は \(\large{a=3}\) となります。

問題.5 平均変化率と微分係数から定数aの決定

本問は、接線の座標に 定数\(\large{a}\) が含まれている場合の問題です。

ある関数の2点を通る直線の傾きは、平均変化率から求められます。

関数\(\large{f(x)=2x^2}\) の \(\large{x=1}\) から \(\large{x=2}\) における平均変化率は、 \begin{eqnarray} \large \frac{f(2)-f(1)}{2-1}&\large =&\large\frac{(2\times2^2)-(2\times1^2)}{1} \\[0.5em] \large &\large =&\large 6 \\[0.5em] \end{eqnarray} となります。

また、\(\large{x=a}\) における接線の傾きは、微分係数から求められます。
関数\(\large{f(x)=2x^2}\) の \(\large{x=a}\) における微分係数を求めると \begin{eqnarray} \large f'(a) &\large =&\large\lim_{h \to 0}\frac{f(a+h)-f(a)}{h} \\[0.5em] \large &\large =&\large \lim_{h \to 0}\frac{2(a+h)^2 - 2a^2}{h} \\[0.5em] \large &\large =&\large \lim_{h \to 0}\frac{4ah+2h^2}{h} \\[0.5em] \large &\large =&\large \lim_{h \to 0}(4a+2h) \\[0.5em] \large &\large =&\large 4a\\[0.5em] \end{eqnarray} となります。

したがって、平均変化率と微分係数が等しいとき $$\large{6=4a}$$ $$\large{a=\frac{3}{2}}$$ となります。

---