1/12公式 | 三次関数と接線に囲まれた面積
本項では、『1/12公式の使い方や導出』 と 『問題の解き方』について解説します。
【1】1/12公式とは
1/12公式とは、三次関数 \(\large{y=ax^3+bx^2+cx+d}\) と その接線に囲まれる面積\(\large{\hspace{1pt}S\hspace{3pt}}\)を瞬時に計算する公式です。
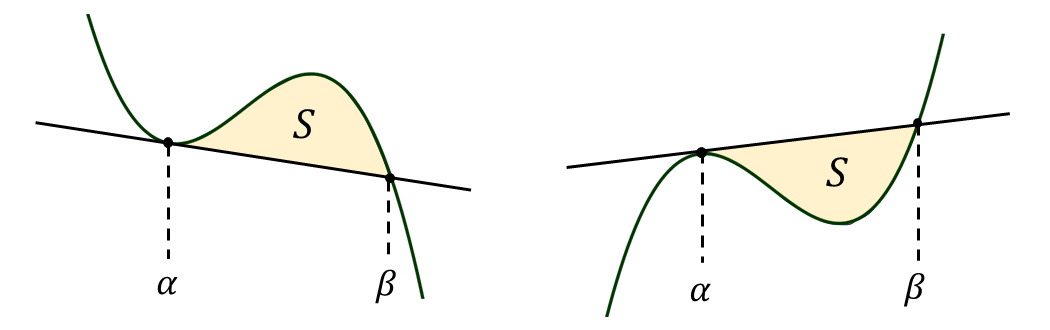
・三次関数上の接線
に囲まれる面積\(\large{\hspace{1pt}S\hspace{2pt}}\)は 接点と交点の\(\large{\hspace{2pt}x\hspace{1pt}}\)座標をそれぞれ \(\large{\alpha, \beta}\) とすると $$\displaystyle\large{S = \frac{|a|}{12}(\beta-\alpha)^4}$$ と求められる
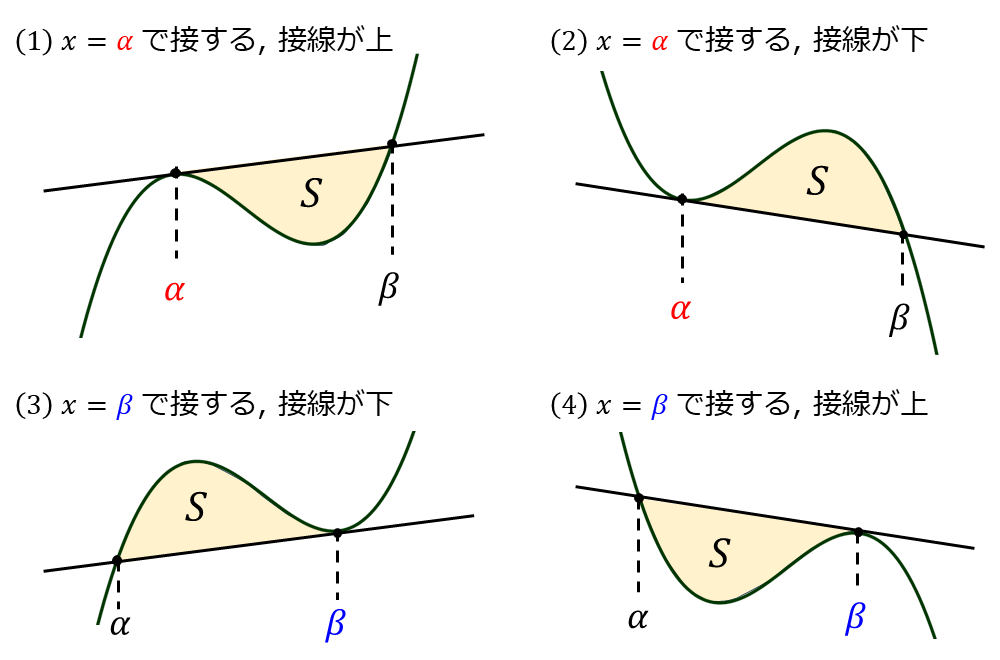
1/12公式は『\(\large{\alpha < \beta}\) のとき 接点が \(\large{x=\alpha}\) または \(\large{x=\beta\hspace{1pt}}\)』 と 『三次関数に対する接線の上下関係』 により場合分けすると 以下の(1)~(4)のパターンが考えられますが、いずれも場合も面積は
$$\large{S = \frac{|a|}{12}(\beta-\alpha)^4}$$
で求めることができます。
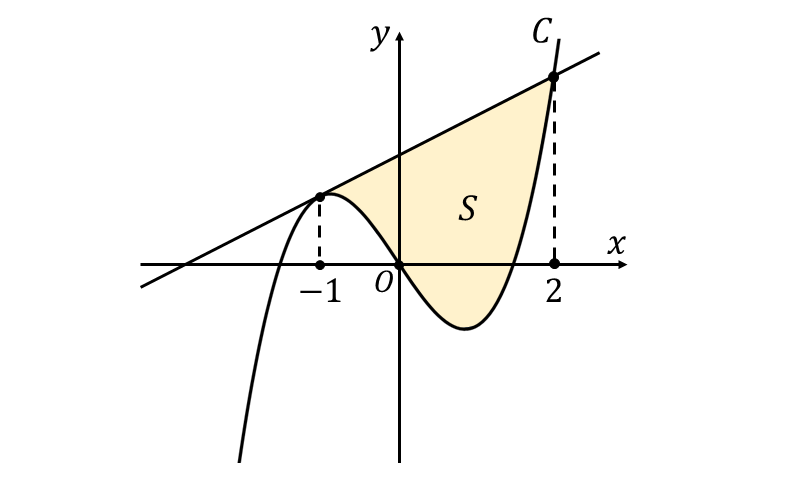
・例題
\(\large{C}\) 上の点\(\large{(\hspace{1pt}-1\hspace{1pt},\hspace{1pt}3\hspace{1pt})}\) における接線 と 曲線 \(\large{C}\) によって囲まれる面積 \(\large{S}\) を求めよ
【解答と解説】
曲線 \(\large{\hspace{2pt}y=2x^3-5x}\) 上の点\(\large{(\hspace{1pt}-1\hspace{1pt},\hspace{1pt}3\hspace{1pt})}\) における接線 と 曲線 \(\large{C}\) によって囲まれる面積 \(\large{S}\) を図示すると、以下のようになります。
まず、曲線\(\large{C}\) 上の点\(\large{(\hspace{1pt}-1\hspace{1pt},\hspace{1pt}3\hspace{1pt})}\) における接線の方程式を求めます。
\(\large{f(x)=2x^3-5x}\) とすると、\(\large{f'(x)=6x^2-5}\) となります。
つまり、点\(\large(-1,3)\) における接線の傾きは \(\large{f'(-1)=1}\) となります。
したがって、接線の方程式の公式 $$\large{y=f'(a)(x-a)+f(a)}$$ から、求める接線の方程式は \begin{eqnarray} \large y &\large =&\large 1 \cdot (x-(-1)) +3 \\[0.5em] \large &\large =&\large x+4\\ \end{eqnarray} と求められます。
\(\large{f(x)=2x^3-5x}\) と 接線\(\large{\hspace{2pt}y=x+4}\) の交点の\(\large{\hspace{1pt}x\hspace{1pt}}\)座標 を求めると \begin{eqnarray} \large 2x^3-5x &\large =&\large x+4 \\[0.5em] \large \large x^3-3x-2 &\large =&\large 0 \\[0.5em] \large \large (x+1)^2(x-2)&\large =&\large 0 \\ \end{eqnarray}
したがって、\(\large{x=-1,\hspace{1pt}2}\) を交点に持つことが分かります。
つまり、1/12公式 $$\large{S = \frac{|a|}{12}(\beta-\alpha)^4}$$ において、三次関数の三次の係数が \(\large{a=2\hspace{1pt}}\)、接点の\(\large{x\hspace{1pt}}\)座標が \(\large{\alpha=-1\hspace{1pt}}\)、交点の\(\large{\hspace{1pt}x\hspace{1pt}}\)座標が\(\large{\hspace{1pt}\beta=2}\) であることから面積は \begin{eqnarray} \large S &\large =&\large \frac{|2|}{12}(2-(-1))^4 \\[0.5em] \large &\large =&\large \frac{27}{2} \\ \end{eqnarray} と求められます。
【別解と解説】
ここで、1/12公式を使わずに面積を求めてみます。(接線の方程式と交点の\(\large{\hspace{1pt}x\hspace{1pt}}\)座標を求めるまでは同じ手順です。)
\(\large{-1 \leqq x \leqq 2}\) において、\(\large{2x^3-5x \leqq x+4}\) であることから、面積\(\large{\hspace{1pt}S\hspace{2pt}}\) は以下のように求められます。
・1/12公式(三次関数と接線)の証明
三次関数を \(\large{f(x)=ax^3+bx^2+cx+d\hspace{1pt}}\)、接線を \(\large{g(x)=px+q\hspace{1pt}}\) とすると \(\large{f(x)}\) と \(\large{g(x)}\) に囲まれる面積\(\large{\hspace{1pt}S\hspace{2pt}}\)が $$\displaystyle\large{S = \frac{|a|}{12}(\beta-\alpha)^4}$$ となることを証明します。
1/12公式は『\(\large{\alpha < \beta}\) のとき 接点が \(\large{x=\alpha}\) または \(\large{x=\beta\hspace{1pt}}\)』 と 『三次関数に対する接線の上下関係』により場合分けすると 以下の(1)~(4)のパターンがあるため、それぞれの場合について示します。
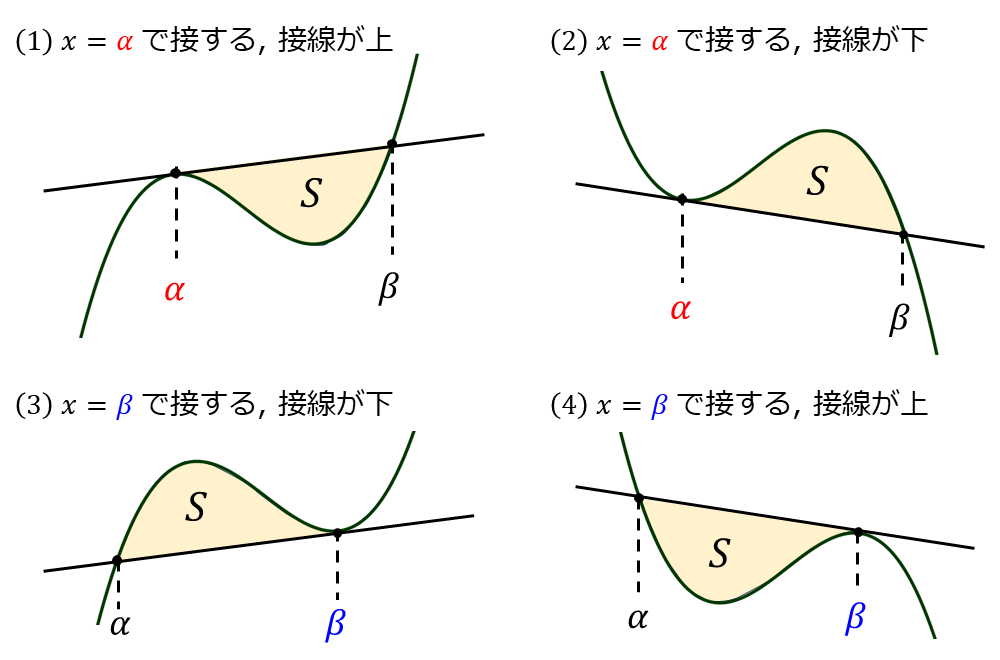
・証明 | (1) x=αで接する, 接線が上の場合
三次関数\(\large{\hspace{1pt}f(x)}\) と 接線\(\large{\hspace{1pt}g(x)}\) が \(\large{x=\alpha}\) で接点を持ち、\(\large{x=\beta}\) で交点を持つ場合、\(\large{g(x)-f(x)}\) は以下のように表されます。 $$\large{g(x)-f(x)=-a(x-\alpha)^2(x-\beta)}$$
\(\large{\alpha \leqq x \leqq \beta}\) において \(\large{g(x) \geqq f(x)}\) であるとき、三次関数 \(\large{f(x)}\) と 接線 \(\large{g(x)}\) で囲まれる面積\(\large{\hspace{1pt}S\hspace{2pt}}\)は、以下のように表せます。 \begin{eqnarray} \large S &\large =& \large \int_\alpha^\beta \{g(x)-f(x)\}\hspace{1pt}dx \\[0.5em] \large &\large =&\large \int_\alpha^\beta -a(x-\alpha)^2(x-\beta) \hspace{1pt}dx \\[0.5em] \large &\large =&\large -a\int_\alpha^\beta (x-\alpha)^2(x-\beta) \hspace{1pt}dx \\[0.5em] \large &\large =&\large -a\int_\alpha^\beta (x-\alpha)^2\{(x-\alpha)-(\beta-\alpha)\} \hspace{1pt}dx \\[0.5em] \large &\large =&\large -a\int_\alpha^\beta \{(x-\alpha)^3-(\beta-\alpha)(x-\alpha)^2\} \hspace{1pt}dx \\[0.5em] \end{eqnarray} ここで、 $$\large{\int (x-\alpha)^n\hspace{1pt}dx = \frac{1}{n+1}(x-\alpha)^{n+1}+C}$$ の関係から、以下のように計算されます。
\begin{eqnarray} \large S &\large =& \large -a\int_\alpha^\beta \{(x-\alpha)^3-(\beta-\alpha)(x-\alpha)^2\} \hspace{1pt}dx \\[0.5em] \large &\large =&\large -a\left[\frac{1}{4}(x-\alpha)^4 -\frac{\beta-\alpha}{3}(x-\alpha)^3 \right]_\alpha^\beta \\[0.7em] \large &\large =&\large -\frac{a}{4}(\beta-\alpha)^4 +\frac{a}{3}(\beta-\alpha)^4 \\[0.7em] \large &\large =&\large \frac{a}{12}(\beta-\alpha)^4 \\[0.5em] \end{eqnarray}・証明 | (2) x=αで接する, 接線が下の場合
\(\large{\alpha \leqq x \leqq \beta}\) において \(\large{g(x) \leqq f(x)}\) であるとき、三次関数\(\large{\hspace{1pt}f(x)}\) と 接線\(\large{\hspace{1pt}g(x)}\) で囲まれる面積\(\large{\hspace{1pt}S\hspace{2pt}}\)は 先述の証明の結果を利用して以下のように求められます。 \begin{eqnarray} \large S &\large =& \large \int_\alpha^\beta \{f(x)-g(x)\}\hspace{1pt}dx \\[0.5em] \large &\large =&\large \int_\alpha^\beta a(x-\alpha)^2(x-\beta) \hspace{1pt}dx \\[0.5em] \large &\large =&\large -\frac{a}{12}(\beta-\alpha)^4 \\[0.5em] \end{eqnarray}
・証明 | (3) x=βで接する, 接線が下の場合
三次関数\(\large{\hspace{1pt}f(x)}\) と 接線\(\large{\hspace{1pt}g(x)}\) が \(\large{x=\beta}\) で接点を持ち、\(\large{x=\alpha}\) で交点を持つ場合、\(\large{f(x)-g(x)}\) は以下のように表されます。 $$\large{f(x)-g(x)=a(x-\alpha)(x-\beta)^2}$$
\(\large{\alpha \leqq x \leqq \beta}\) において \(\large{f(x) \geqq g(x)}\) であるとき、三次関数 \(\large{f(x)}\) と 接線 \(\large{g(x)}\) で囲まれる面積\(\large{\hspace{1pt}S\hspace{2pt}}\)は、以下のように表せます。 \begin{eqnarray} \large S &\large =& \large \int_\alpha^\beta \{f(x)-g(x)\}\hspace{1pt}dx \\[0.5em] \large &\large =&\large \int_\alpha^\beta a(x-\alpha)(x-\beta)^2 \hspace{1pt}dx \\[0.5em] \large &\large =&\large a\int_\alpha^\beta (x-\alpha)(x-\beta)^2 \hspace{1pt}dx \\[0.5em] \large &\large =&\large a\int_\alpha^\beta \{(x-\beta)-(\alpha-\beta)\}(x-\beta)^2 \hspace{1pt}dx \\[0.5em] \large &\large =&\large a\int_\alpha^\beta \{(x-\beta)^3-(\alpha-\beta)(x-\beta)^2\} \hspace{1pt}dx \\[0.5em] \end{eqnarray} ここで、 $$\large{\int (x-\alpha)^n\hspace{1pt}dx = \frac{1}{n+1}(x-\alpha)^{n+1}+C}$$ の関係から、以下のように計算されます。
\begin{eqnarray} \large S &\large =& \large a\int_\alpha^\beta \{(x-\beta)^3-(\alpha-\beta)(x-\beta)^2\} \hspace{1pt}dx \\[0.5em] \large &\large =&\large a\left[\frac{1}{4}(x-\beta)^4 -\frac{\alpha-\beta}{3}(x-\beta)^3 \right]_\alpha^\beta \\[0.7em] \large &\large =&\large -\frac{a}{4}(\beta-\alpha)^4 +\frac{a}{3}(\beta-\alpha)^4 \\[0.7em] \large &\large =&\large \frac{a}{12}(\beta-\alpha)^4 \\[0.5em] \end{eqnarray}・証明 | (4) x=βで接する, 接線が上の場合
\(\large{\alpha \leqq x \leqq \beta}\) において \(\large{f(x) \leqq g(x)}\) であるとき、三次関数 \(\large{f(x)}\) と 接線 \(\large{g(x)}\) で囲まれる面積\(\large{\hspace{1pt}S\hspace{2pt}}\)は 先述の証明の結果を利用して以下のように求められます。 \begin{eqnarray} \large S &\large =& \large \int_\alpha^\beta \{g(x)-f(x)\}\hspace{1pt}dx \\[0.5em] \large &\large =&\large \int_\alpha^\beta -a(x-\alpha)(x-\beta)^2 \hspace{1pt}dx \\[0.5em] \large &\large =&\large -\frac{a}{12}(\beta-\alpha)^4 \\[0.5em] \end{eqnarray} 証明(1)~(4)の結果から、三次関数\(\large{\hspace{1pt}f(x)}\) と 接線\(\large{\hspace{1pt}g(x)}\) によって囲まれる面積\(\large{\hspace{1pt}S\hspace{2pt}}\)は、接点と交点の\(\large{\hspace{2pt}x\hspace{1pt}}\)座標をそれぞれ \(\large{\alpha, \beta}\) とすると $$\large{S=\frac{|a|}{12}(\beta-\alpha)^4}$$ となることが示されます。
・証明の補足
証明の途中計算で以下の不定積分の式を使用しました。 $$\large{\int (x-\alpha)^n\hspace{1pt}dx = \frac{1}{n+1}(x-\alpha)^{n+1}+C}$$
上式を 置換積分法により導きます。
まず \(\large{x-\alpha =t }\) とおき、 \(\large{x =t+\alpha }\) の両辺を \(\large{t}\) で微分すると
$$\large{\frac{dx}{dt} = 1}$$
となります。すなわち、\(\large{dx = dt}\) と表せます。
つまり、左辺の積分を計算すると \begin{eqnarray} \large \int (x-\alpha)^n\hspace{1pt}dx &\large =&\large \int t^n\hspace{1pt}dt \\[0.5em] \large &\large =&\large \frac{1}{n+1}t^{n+1} +C\\[0.5em] \large &\large =&\large \frac{1}{n+1}(x-\alpha)^{n+1} +C\\[0.5em] \end{eqnarray} となることから、以下の不定積分が導かれます。 $$\large{\int (x-\alpha)^n\hspace{1pt}dx = \frac{1}{n+1}(x-\alpha)^{n+1}+C}$$
【2】問題と解き方
本章では、1/12公式 に関連した問題について解説します。
\(\large{C}\) 上の点\(\large{(\hspace{1pt}-2\hspace{1pt},\hspace{1pt}1\hspace{1pt})}\) における接線 と 曲線 \(\large{C}\) によって囲まれる面積 \(\large{S}\) を求めよ
曲線 \(\large{C}\) と 点\(\large{(0,2)}\) から引いた曲線 \(\large{C}\) の接線によって囲まれる面積 \(\large{S}\) を求めよ
問題(1) | 三次関数と接線に囲まれた面積
\(\large{C}\) 上の点\(\large{(\hspace{1pt}-2\hspace{1pt},\hspace{1pt}1\hspace{1pt})}\) における接線 と 曲線 \(\large{C}\) によって囲まれる面積 \(\large{S}\) を求めよ
【解答と解説】
曲線 \(\large{\hspace{2pt}y=x^3+4x^2+3x-1}\) 上の点\(\large{(\hspace{1pt}-2\hspace{1pt},\hspace{1pt}1\hspace{1pt})}\) における接線 と 曲線 \(\large{C}\) によって囲まれる面積 \(\large{S}\) を図示すると、以下のようになります。
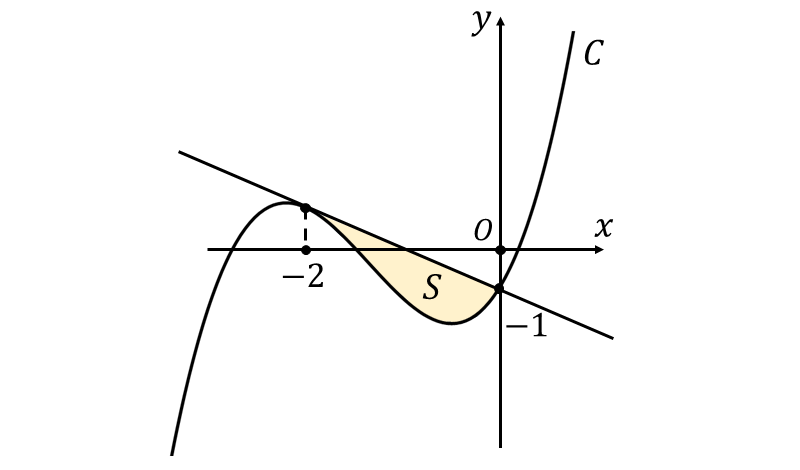
まず、曲線\(\large{C}\) 上の点\(\large{(\hspace{1pt}-2\hspace{1pt},\hspace{1pt}1\hspace{1pt})}\) における接線の方程式を求めます。
\(\large{f(x)=x^3+4x^2+3x-1}\) とすると、\(\large{f'(x)=3x^2+8x+3}\) となります。
つまり、点\(\large(-2,1)\) における接線の傾きは \(\large{f'(-2)=-1}\) となります。
したがって、接線の方程式の公式 $$\large{y=f'(a)(x-a)+f(a)}$$ から、求める接線の方程式は \begin{eqnarray} \large y &\large =&\large -1 \cdot (x-(-2)) +1 \\[0.5em] \large &\large =&\large -x-1\\ \end{eqnarray} と求められます。
三次関数\(\large{\hspace{2pt}f(x)=x^3+4x^2+3x-1}\) と 接線\(\large{\hspace{2pt}y=-x-1}\) の交点の\(\large{\hspace{1pt}x\hspace{1pt}}\)座標 を求めると \begin{eqnarray} \large x^3+4x^2+3x-1 &\large =&\large -x-1 \\[0.5em] \large \large x^3+4x^2+4x&\large =&\large 0 \\[0.5em] \large \large x(x+2)^2&\large =&\large 0 \\ \end{eqnarray}
したがって、交点の\(\large{\hspace{1pt}x\hspace{1pt}}\)座標は \(\large{x=-2,\hspace{1pt}0}\) となります。
つまり、1/12公式 $$\large{S = \frac{|a|}{12}(\beta-\alpha)^4}$$ において、三次関数の三次の係数が \(\large{a=1}\)、接点の\(\large{x\hspace{1pt}}\)座標が \(\large{\alpha=-2}\) 、交点の\(\large{x\hspace{1pt}}\)座標が\(\large{\hspace{1pt}\beta=0}\) であることから面積は \begin{eqnarray} \large S &\large =&\large \frac{|1|}{12}(0-(-2))^4 \\[0.5em] \large &\large =&\large \frac{4}{3} \\ \end{eqnarray} と求められます。
【別解と解説】
ここで、1/12公式を使わずに面積を求めてみます。(接線の方程式と交点の\(\large{\hspace{1pt}x\hspace{1pt}}\)座標を求めるまでは同じ手順です。)
\(\large{-2 \leqq x \leqq 0}\) において、\(\large{x^3+4x^2+3x-1 \leqq -x-1}\) であることから、面積\(\large{\hspace{1pt}S\hspace{2pt}}\) は以下のように求められます。
問題(2) | 三次関数と接線に囲まれた面積
曲線 \(\large{C}\) と 点\(\large{(0,2)}\) から引いた曲線 \(\large{C}\) の接線によって囲まれる面積 \(\large{S}\) を求めよ
【解答と解説】
まず、曲線\(\large{C}\) 上の点\(\large{(\hspace{1pt}t\hspace{1pt},\hspace{1pt}-t^3+4t\hspace{1pt})}\) における接線の方程式を求めます。
\(\large{f(x)=-x^3+4x}\) とすると、\(\large{f'(x)=-3x^2+4}\) となります。
つまり、点\(\large(\hspace{1pt}t\hspace{1pt},\hspace{1pt}-t^3+4t\hspace{1pt})\) における接線の傾きは \(\large{f'(t)=-3t^2+4}\) となります。
したがって、接線の方程式の公式 $$\large{y=f'(a)(x-a)+f(a)}$$ から、接線の方程式は $$\large{y=(-3t^2+4)(x-t)-t^3+4t \hspace{5pt}\cdots(1)}$$ となります。
ここで、(1)式が 点\(\large{(0,2)}\) を通るという条件から、三次関数上の接点の座標を求めます。 \begin{eqnarray} \large 2 &\large =&\large (-3t^2+4)(0-t)-t^3+4t \\[0.5em] \large \large t^3 &\large =&\large 1 \\[0.5em] \large \large t &\large =&\large 1 \\ \end{eqnarray}
したがって、点\(\large{(0,2)\hspace{1pt}}\)を通る接線は、三次関数と点\(\large{(1,3)}\) で接します。
このとき、接線の方程式は以下のようになります。 $$\large{y=x + 2}$$
三次関数\(\large{\hspace{1pt}y=-x^3+4x}\) と 接線\(\large{\hspace{1pt}y=x + 2}\) の交点を求めると、 \begin{eqnarray} \large -x^3+4x &\large =&\large x + 2 \\[0.5em] \large \large x^3-3x +2 &\large =&\large 0 \\[0.5em] \large \large (x-1)^2(x+2) &\large =&\large 0 \\ \end{eqnarray}
つまり、三次関数\(\large{\hspace{1pt}y=-x^3+4x}\) と 接線\(\large{\hspace{1pt}y=x + 2}\) は接点の他に \(\large{x=-2}\) において交点を持ちます。
ここで、三次関数と接線によって囲まれた面積\(\large{\hspace{1pt}S\hspace{2pt}}\)を図示すると、以下のようになります。
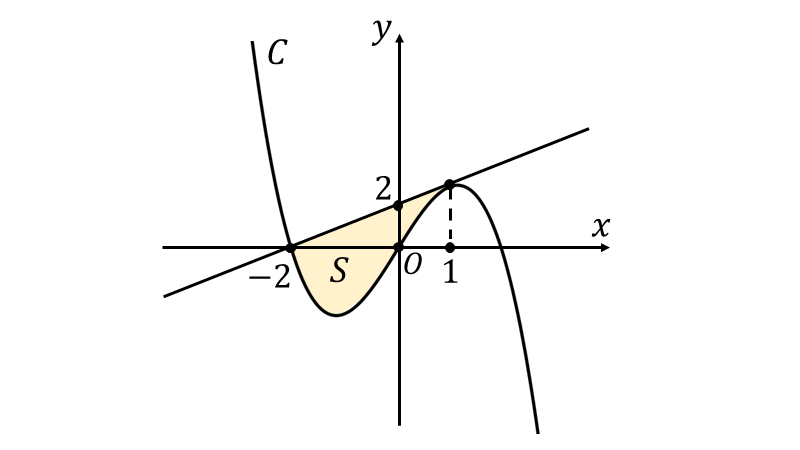
1/12公式 $$\large{S = \frac{|a|}{12}(\beta-\alpha)^4}$$ において、三次関数の三次の係数が \(\large{a=-1}\)、接点の\(\large{x\hspace{1pt}}\)座標が \(\large{\beta=1}\) 、交点の\(\large{x\hspace{1pt}}\)座標が\(\large{\hspace{1pt}\alpha=-2}\) であることから面積は \begin{eqnarray} \large S &\large =&\large \frac{|-1|}{12}(1-(-2))^4 \\[0.5em] \large &\large =&\large \frac{27}{4} \\ \end{eqnarray} と求められます。
【別解と解説】
ここで、1/12公式を使わずに面積を求めてみます。(接線の方程式と交点の\(\large{\hspace{1pt}x\hspace{1pt}}\)座標を求めるまでは同じ手順です。)
\(\large{-2 \leqq x \leqq 1}\) において、\(\large{-x^3+4x \leqq x+2}\) であることから、面積\(\large{\hspace{1pt}S\hspace{2pt}}\) は以下のように求められます。