接線の方程式
本項では、『接線の方程式』 と 『問題の解き方』について解説します。
【1】接線の方程式
関数 \(\large{y=f(x)}\) が \(\large{x=a}\) で微分可能であるとき、\(\large{x=a}\) における接線は以下のように表されます。
【1-1】接線の方程式の導出
点\(\large{(x_1 , y_1)}\) を通り、傾き\(\large{m}\) であるような直線の方程式は以下の式によって表されます。 $$\large{y - y_1 = m (x-x_1) \cdots(1)}$$
ここで、関数 \(\large{y=f(x)}\) の 微分係数 \(\large{f'(a)}\) は、点\(\large{(a,f(a))}\) における接線の傾きを表します。
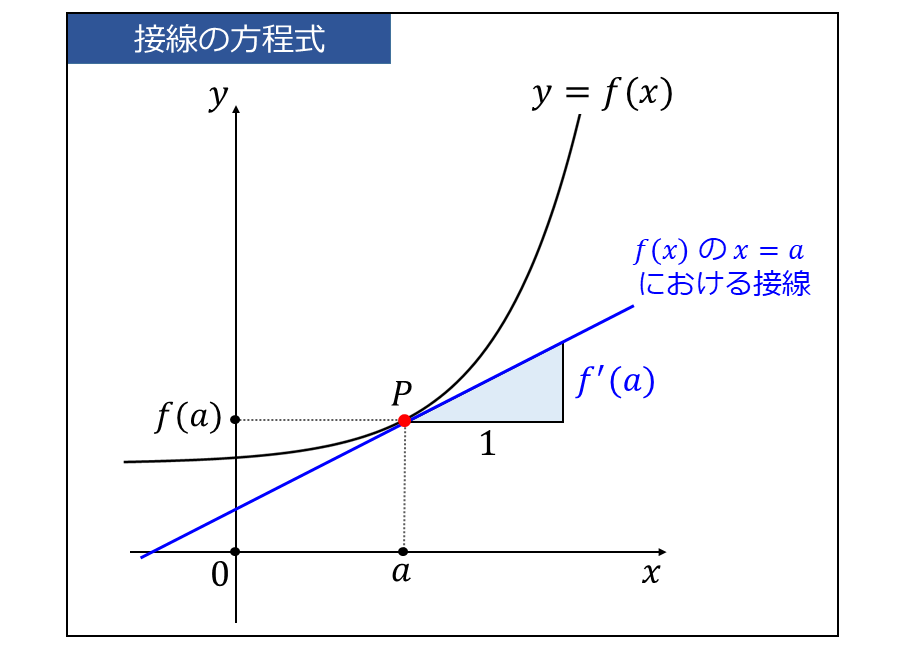
つまり、点\(\large{(a,f(a))}\) を通る傾き \(\large{f'(a)}\) の接線の方程式は、(1)式の変数と以下の関係があります。 $$\large{x_1 = a}$$ $$\large{y_1 = f(a)}$$ $$\large{m = f'(a)}$$ したがって、\(\large{y=f(x)}\) の \(\large{x=a}\) における接線の方程式は、以下のようになります。 $$\large{y= f'(a)(x-a)+f(a)}$$
【1-2】例題
例えば、以下のような問題について考えます。
\(\displaystyle \large{y=x^3-2x}\)
\(\large{f(x)=x^3-2x}\) とすると、\(\large{f'(x)=3x-2}\) となります。
つまり、点\(\large(2,4)\) における微分係数は \(\large{f'(2)=4}\) となります。
したがって、接線の方程式の公式 $$\large{y=f'(a)(x-a)+f(a)}$$ から、求める接線の方程式は $$\large{y=4(x-2)+4}$$ すなわち $$\large{y=4x-4}$$ となります。
【2】円の接線の方程式
円の接線の方程式は、以下の式により表されます。
【2-1】円の接線の方程式の導出
円 \(\large{x^2+y^2=r^2}\) 上の点\(\large{(x_1,y_1)}\) を通る円の接線の方程式は以下のように導出されます。
円の方程式 \(\large{x^2+y^2=r^2}\) (\(\large{r>0}\)) の両辺を \(\large{x}\) について微分すると、合成関数の微分から、 $$\large{2x + 2y\cdot y\hspace{1pt}' = 0}$$ つまり、\(\large{y \neq 0}\) のとき、 $$\large{y\hspace{1pt}' = -\frac{x}{y}}$$ となります。
ここで、接線の公式から、接線の方程式は \(\large{y_1 \neq 0}\) のとき、 $$\large{y = -\frac{x_1}{y_1}(x-x_1)+y_1}$$ となります。上式を整理すると、 $$\large{x_1 x + y_1 y = {x_1}^2+{y_1}^2}$$ ここで、点\(\large{(x_1,y_1)}\) は 半径\(\large{r}\) の円上の点であるため、\(\large{{x_1}^2+{y_1}^2=r^2}\) が成り立ちます。
したがって、\(\large{y_1 \neq 0}\) のとき、円の接線の方程式は $$\large{x_1 x + y_1 y =r^2 \cdots (2)}$$ となります。
ここで、\(\large{y_1=0}\) の場合は、\(\large{x_1 =\pm\hspace{1pt} r}\) のとき \(\large{x = \pm\hspace{1pt} r}\) が接線となります。
したがって、この場合も(2)式に含まれます。
以上から、円の接線の方程式は $$\large{x_1 x + y_1 y =r^2}$$ となります。
【2-2】例題
例えば、以下のような問題について考えます。
\(\displaystyle \large{x^2 + y^2 = 4}\)
円 \(\large{x^2+y^2=r^2}\) 上の点\(\large{(x_1,y_1)}\) を通る接線の方程式の公式 $$\large{x_1 x + y_1 y =r^2}$$ から、求める接線は \(\large{x_1 = 1}\)、\(\large{y_1 = \sqrt{3}}\)、\(\large{r=2}\) であるため $$\large{x+\sqrt{3}y = 4}$$ すなわち $$\large{y = -\frac{\sqrt{3}}{3}x+\frac{4\sqrt{3}}{3}}$$ となります。
【3】問題と解き方
本章では、接線の方程式 に関連した問題について解説します。
・基礎問題 (1)~(5)
\(\displaystyle \large{y=\frac{2}{x+1}}\)
\(\displaystyle \large{y=\sin x}\)
\(\displaystyle \large{y=\log x}\)
問題(1)~(3)は、曲線上の点における接線の方程式を求める問題です。
(解答と解説 : 問題(1) 問題(2) 問題(3))
\(\displaystyle \large{x^2+y^2=1}\)
\(\displaystyle \large{\frac{x^2}{4}+\frac{y^2}{3}=1}\)
問題(4)、(5)は、円や楕円の接線の方程式を求める問題です。
(解答と解説 : 問題(4) 問題(5))
・応用問題 (6)~(8)
\(\displaystyle \large{y = e^x}\)
問題(6)は、曲線外の点から引いた接線を求める問題です。
(解答と解説 : 問題(6))
\(\displaystyle \large{y = \log x}\)
問題(7)は、傾きがわかっている接線を求める問題です。
(解答と解説 : 問題(7))
問題(8)は、2つの曲線に共通する接線を求める問題です。
(解答と解説 : 問題(8))
問題(1) 分数関数の接線の方程式
\(\displaystyle \large{y=\frac{2}{x+1}}\)
【解答と解説】
本問は、分数関数の接線を求める問題です。
\(\displaystyle\large{f(x)=\frac{2}{x+1}}\) とすると、\(\displaystyle\large{f'(x)=-\frac{2}{(x+1)^2}}\) となります。
つまり、点\(\large(1,1)\) における微分係数は \(\displaystyle\large{f'(1)=-\frac{1}{2}}\) となります。
したがって、接線の方程式の公式 $$\large{y=f'(a)(x-a)+f(a)}$$ から、求める接線の方程式は $$\large{y=-\frac{1}{2}(x-1)+1}$$ すなわち $$\large{y=-\frac{1}{2}x+\frac{3}{2}}$$ となります。
問題(2) 三角関数の接線の方程式
\(\displaystyle \large{y=\sin x}\)
【解答と解説】
本問は、三角関数の接線を求める問題です。
\(\displaystyle\large{f(x)=\sin x}\) とすると、三角関数の微分から $$\large{f'(x)=\cos x}$$ となります。
すなわち、点\(\large(0,0)\) における微分係数は \(\displaystyle\large{f'(0)=1}\) となります。
したがって、接線の方程式の公式 $$\large{y=f'(a)(x-a)+f(a)}$$ から、求める接線の方程式は $$\large{y=1\cdot(x-0)+0}$$ すなわち $$\large{y=x}$$ となります。
問題(3) 対数関数の接線の方程式
\(\displaystyle \large{y=\log x}\)
【解答と解説】
本問は、対数関数の接線を求める問題です。
\(\displaystyle\large{f(x)=\log x}\) とすると、対数関数の微分から $$\large{f'(x)=\frac{1}{x}}$$ となります。
すなわち、点\(\large(e,1)\) における微分係数は \(\displaystyle\large{f'(e)=\frac{1}{e}}\) となります。
したがって、接線の方程式の公式 $$\large{y=f'(a)(x-a)+f(a)}$$ から、求める接線の方程式は $$\large{y=\frac{1}{e}(x-e)+1}$$ すなわち $$\large{y=\frac{1}{e}x}$$ となります。
問題(4) 円の接線の方程式
\(\displaystyle \large{x^2+y^2=1}\)
【解答と解説】
本問は、円の方程式の接線を求める問題です。
円 \(\large{x^2+y^2=r^2}\) 上の点\(\large{(x_1,y_1)}\) を通る接線の方程式の公式 $$\large{x_1 x + y_1 y =r^2}$$ から、求める接線は \(\displaystyle\large{x_1 = \frac{\sqrt{3}}{2}}\)、\(\displaystyle\large{y_1 =\frac{1}{2}}\)、\(\large{r=1}\) であるため $$\large{\frac{\sqrt{3}}{2}x+\frac{1}{2}y = 1}$$ すなわち $$\large{y = -\sqrt{3}x + 2}$$ となります。
【別解】
円の接線の公式を使用しない場合は、以下のように求められます。
円の方程式 \(\large{x^2+y^2=1}\) を \(\large{x}\) について微分すると、合成関数の微分から、 $$\large{2x + 2y\cdot y\hspace{1pt}' = 0}$$ したがって、\(\large{y\neq 0}\) であるとすると、 $$\large{y' = -\frac{x}{y}}$$ となります。
すなわち、点\(\displaystyle\large{\left(\frac{\sqrt{3}}{2},\frac{1}{2}\right)}\) における接線の傾きは、\(\large{-\sqrt{3}}\) となります。
したがって、接線の方程式の公式 $$\large{y=f'(a)(x-a)+f(a)}$$ から、求める接線の方程式は $$\large{y=-\sqrt{3}\left(x-\frac{\sqrt{3}}{2}\right)+\frac{1}{2}}$$ すなわち $$\large{y=-\sqrt{3}x+2}$$ となります。
問題(5) 楕円の接線の方程式
\(\displaystyle \large{\frac{x^2}{4}+\frac{y^2}{3}=1}\)
【解答と解説】
本問は、楕円の方程式の接線を求める問題です。
楕円の方程式 \(\displaystyle\large{\frac{x^2}{4}+\frac{y^2}{3}=1}\) を \(\large{x}\) について微分すると、合成関数の微分から、 $$\large{\frac{2x}{4} + \frac{2y}{3}\cdot y\hspace{1pt}' = 0}$$ したがって、\(\large{y\neq 0}\) であるとすると、 $$\large{y' = -\frac{3x}{4y}}$$ となります。
すなわち、点\(\displaystyle\large{\left(\sqrt{3},\frac{\sqrt{3}}{2}\right)}\) における接線の傾きは、\(\displaystyle\large{-\frac{3}{2}}\) となります。
したがって、接線の方程式の公式 $$\large{y=f'(a)(x-a)+f(a)}$$ から、求める接線の方程式は $$\large{y=-\frac{3}{2}(x-\sqrt{3})+\frac{\sqrt{3}}{2}}$$ すなわち $$\large{y=-\frac{3}{2}x+2\sqrt{3}}$$ となります。
問題(6) 曲線外の点から引いた接線
\(\displaystyle \large{y = e^x}\)
【解答と解説】
本問は、曲線外の点から接線の方程式を求める問題です。
このような問題では、接点が分からないため、接点を \(\large{(a,f(a))}\) とおき、接線が点\(\large{(1,0)}\) を通る条件から接線の方程式を求めます。
\(\large{y= e^x}\) を微分すると、 $$\large{y\hspace{1pt}' = e^x }$$ となります。
つまり、接点を \(\large{(a,e^a)}\) とすると、接線の傾きは \(\large{e^a}\) となります。
したがって、接線の方程式は以下のようになります。 $$\large{y = e^a (x-a) + e^a}$$
上記の接線の方程式が点\(\displaystyle\large{(1,0)}\) を通るという条件から、 $$\large{0 = e^a (1-a) + e^a}$$ $$\large{0 = e^a (2-a) }$$ 上式から、\(\large{a=2}\) となります。
したがって、求める接線の方程式は、 $$\large{y=e^2(x-2)+e^2}$$ すなわち、 $$\large{y=e^2(x-1)}$$ となります。
問題(7) 傾きがわかっている接線の方程式
\(\displaystyle \large{y = \log x}\)
本問は、接点が分かりませんが、傾きがわかっている場合の接線の方程式の問題です。
\(\displaystyle\large{f(x)=\log x}\) とすると、対数関数の微分から $$\large{f'(x)=\frac{1}{x}}$$ となります。
接点を \(\large{(a,\log a)}\) とおくと、接線の傾きが \(\large{e}\) であるため、 $$\large{f'(a)=\frac{1}{a} = e}$$ を満たします。上式から、\(\large{a}\)を求めると $$\large{a=\frac{1}{e} }$$ となります。
したがって、点\(\displaystyle\large{\left(\frac{1}{e},\hspace{2pt}\log \frac{1}{e}\right)=\left(\frac{1}{e},\hspace{2pt}-1\right)}\) における傾き \(\large{e}\) の直線が求める接線となるので、求める接線の方程式は $$\large{y = e\left(x-\frac{1}{e}\right)-1}$$ すなわち、 $$\large{y = ex -2}$$ が求める接線の方程式となります。
問題(8) 2つの曲線に共通する接線の方程式
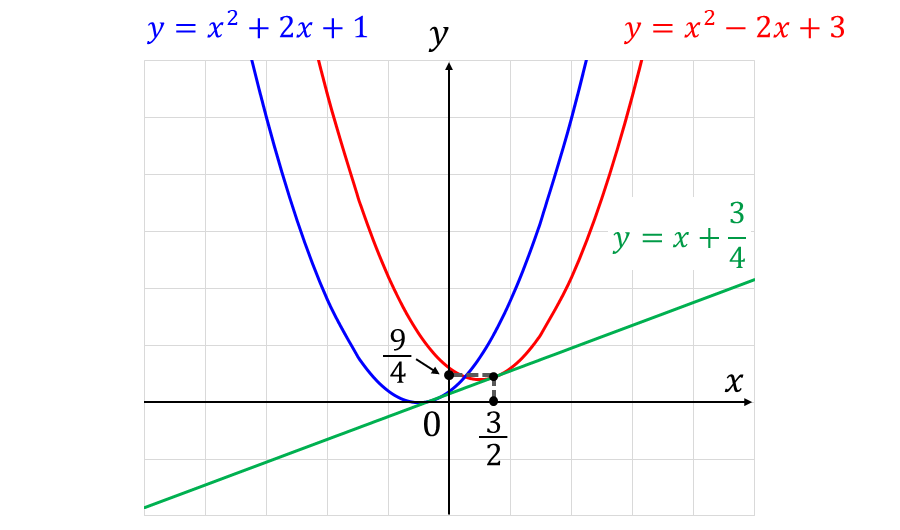
本問は、2つの曲線に共通する接線を求める問題です。
\(\displaystyle\large{f(x)=x^2-2x+3}\)、\(\displaystyle\large{g(x)=x^2+2x+1}\) とすると、 $$\large{f'(x)=2x-2}$$ $$\large{g'(x)=2x+2}$$ となります。
ここで、\(\displaystyle\large{f(x)=x^2-2x+3}\) が 接点\(\large{(\hspace{1pt}a,a^2-2a+3\hspace{1pt})}\) に接線をもつとすると、接線の方程式は $$\large{y = 2(a-1)(x-a)+a^2-2a+3}$$ すなわち、 $$\large{y = 2(a-1)x-a^2+3\hspace{10pt}\cdots(3)}$$ となります。
一方、\(\displaystyle\large{g(x)=x^2+2x+1}\) が 接点\(\large{(\hspace{1pt}b,b^2+2b+1\hspace{1pt})}\) に接線をもつとすると、接線の方程式は $$\large{y = 2(b+1)(x-b)+b^2+2b+1}$$ すなわち、 $$\large{y = 2(b+1)x-b^2+1\hspace{10pt}\cdots(4)}$$ となります。
ここで、(3)式と(4)式が一致するためには、 $$\large{2(a-1) = 2(b+1)}$$ $$\large{-a^2+3 = -b^2+1}$$
上式を解くと、\(\displaystyle\large{a=\frac{3}{2},\hspace{1pt}b=-\frac{1}{2}}\) となります。
したがって、\(\displaystyle\large{f(x)=x^2-2x+3}\) は、点\(\displaystyle\large{\left(\frac{3}{2},\frac{9}{4}\right)}\) に傾き \(\large{1}\) の接線を持つため、 $$\large{y = 1\cdot\left(x-\frac{3}{2}\right)+\frac{9}{4}}$$ すなわち、 $$\large{y = x +\frac{3}{4}}$$ が求める接線となります。
下図に問題の2つの関数と共通する接線を描いた図を示します。