法線の方程式
本項では、『法線の方程式』 と 『問題の解き方』について解説します。
【1】法線の方程式
曲線 \(\large{y=f(x)}\) が \(\large{x=a}\) で微分可能であるとき、\(\large{x=a}\) における法線は以下の式により求められます。
【1-1】法線の方程式の導出
曲線 \(\large{y=f(x)}\) において \(\large{x=a}\) における接線の方程式は以下のように表されます。 $$\large{y= f'(a)(x-a)+f(a)}$$
ここで、下図のような接線と垂直に交わる直線のことを法線といいます。
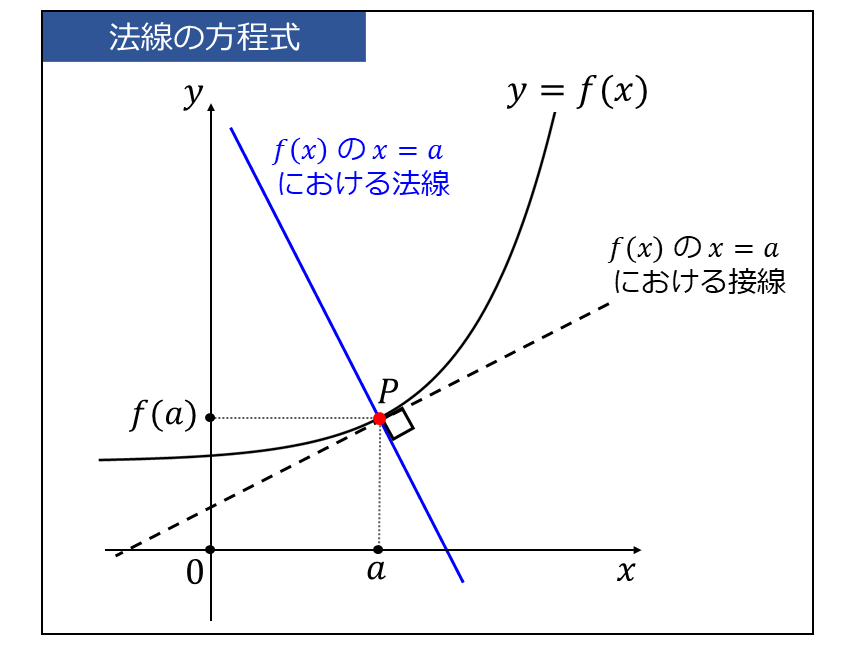
垂直に交わる2つの直線の傾きの積は、\(\large{-1}\) となる性質があります。
したがって、法線の傾きを \(\large{m}\) とすると、接線の傾きが \(\large{f'(a)}\) であることから、\(\large{f'(a) \neq 0}\) のとき
$$\large{m \cdot f'(a) = -1}$$
$$\large{m=-\frac{1}{f'(a)}}$$
と求めることができます。
よって、接点 \(\large{(a,f(a))}\) を通り、接線と垂直に交わる法線は、以下の式により表されます。 $$\large{y= -\frac{1}{f'(a)}(x-a)+f(a)}$$
【1-2】例題
例えば、以下のような関数の法線を求めます。
\(\displaystyle \large{y=x^3+x}\)
\(\large{f(x)=x^3+x}\) とおくと、\(\large{f'(x)=3x+1}\) となります。
つまり、点\(\large(1,2)\) における微分係数は \(\large{f'(1)=4}\) となります。
したがって、法線の方程式の公式 $$\large{y=-\frac{1}{f'(a)}(x-a)+f(a)}$$ から、求める法線の方程式は $$\large{y=-\frac{1}{4}(x-1)+2}$$ すなわち $$\large{y=-\frac{1}{4}x+\frac{9}{4}}$$ となります。
【2】問題と解き方
本章では、法線の方程式 に関連した問題について解説します。
\(\displaystyle \large{y=\frac{1}{x-2}}\)
\(\displaystyle \large{y=\cos x}\)
\(\displaystyle \large{y=e^{-2x}}\)
\(\displaystyle \large{y=\log x^2}\)
問題(1)~(4)は、曲線上の点における法線の方程式を求める問題です。
(解答と解説 : 問題(1) 問題(2) 問題(3) 問題(4))
\(\displaystyle \large{x^2+y^2=9}\)
問題(5)は、円上の点における法線の方程式を求める問題です。
(解答と解説 : 問題(5))
問題(1) 分数関数の法線の方程式
\(\displaystyle \large{y=\frac{1}{x-2}}\)
【解答と解説】
本問は、分数関数の法線を求める問題です。
\(\displaystyle\large{f(x)=\frac{1}{x-2}}\) とすると、\(\displaystyle\large{f'(x)=-\frac{1}{(x-2)^2}}\) となります。
つまり、点\(\large(3,1)\) における微分係数は \(\displaystyle\large{f'(3)=-1}\) となります。
したがって、法線の方程式の公式 $$\large{y=-\frac{1}{f'(a)}(x-a)+f(a)}$$ から、求める法線の方程式は $$\large{y=1 \cdot (x-3)+1}$$ すなわち $$\large{y=x -2}$$ となります。
問題(2) 三角関数の法線の方程式
\(\displaystyle \large{y=\cos x}\)
【解答と解説】
本問は、三角関数の法線を求める問題です。
\(\displaystyle\large{f(x)=\cos x}\) とすると、三角関数の微分から $$\large{f'(x)=-\sin x}$$ となります。
すなわち、点\(\displaystyle\large{\left(\frac{\pi}{3},\frac{1}{2}\right)}\) における微分係数は \(\displaystyle\large{f'\left(\frac{\pi}{3}\right)=-\frac{\sqrt{3}}{2}}\) となります。
したがって、法線の方程式の公式 $$\large{y=-\frac{1}{f'(a)}(x-a)+f(a)}$$ から、求める法線の方程式は $$\large{y= \frac{2}{\sqrt{3}}\cdot (x-\frac{\pi}{3})+\frac{1}{2}}$$ すなわち $$\large{y=\frac{2\sqrt{3}}{3}x + \frac{9-4\sqrt{3}\pi}{18}}$$ となります。
問題(3) 指数関数の法線の方程式
\(\displaystyle \large{y=e^{-2x}}\)
【解答と解説】
本問は、指数関数の法線を求める問題です。
\(\displaystyle\large{f(x)=e^{-2x}}\) とすると、 $$\large{f'(x)=e^{-2x} \cdot (-2) = -2e^{-2x}}$$ となります。
すなわち、点\(\large(-1,e^2)\) における微分係数は \(\displaystyle\large{f'(-1)=-2e^2}\) となります。
したがって、法線の方程式の公式 $$\large{y=-\frac{1}{f'(a)}(x-a)+f(a)}$$ から、求める法線の方程式は $$\large{y= \frac{1}{2e^2}\cdot (x+1)+e^2}$$ すなわち $$\large{y=\frac{1}{2e^2}x + \frac{1+2e^4}{2e^2}}$$ となります。
問題(4) 対数関数の法線の方程式
\(\displaystyle \large{y=\log x^2}\)
【解答と解説】
本問は、対数関数の法線を求める問題です。
\(\displaystyle\large{f(x)=\log x^2}\) とすると、対数関数の微分から $$\large{f'(x)=\frac{1}{x^2} \cdot 2x = \frac{2}{x}}$$ となります。
すなわち、点\(\large(e,2)\) における微分係数は \(\displaystyle\large{f'(e)=\frac{2}{e}}\) となります。
したがって、法線の方程式の公式 $$\large{y=-\frac{1}{f'(a)}(x-a)+f(a)}$$ から、求める法線の方程式は $$\large{y= -\frac{e}{2}\cdot (x-e)+2}$$ すなわち $$\large{y=-\frac{e}{2}x + \frac{e^2}{2}+2}$$ となります。
問題(5) 円の法線の方程式
\(\displaystyle \large{x^2+y^2=9}\)
【解答と解説】
本問は、円の方程式の法線を求める問題です。
円の方程式 \(\large{x^2+y^2=9}\) を \(\large{x}\) について微分すると、合成関数の微分から、 $$\large{2x + 2y\cdot y\hspace{1pt}' = 0}$$ したがって、\(\large{y\neq 0}\) であるとすると、 $$\large{y\hspace{1pt}' = -\frac{x}{y}}$$ となります。
すなわち、点\(\displaystyle\large{(2,\sqrt{5})}\) における微分係数は、\(\displaystyle\large{-\frac{2}{\sqrt{5}}}\) となります。
したがって、法線の方程式の公式 $$\large{y=-\frac{1}{f'(a)}(x-a)+f(a)}$$ から、求める法線の方程式は $$\large{y=\frac{\sqrt{5}}{2}(x-2)+\sqrt{5}}$$ すなわち $$\large{y=\frac{\sqrt{5}}{2}x}$$ となります。