導関数の定義

本項では、『導関数の定義』 と 『問題の解き方』について解説します。

【1】導関数の定義

微分係数 \(\large{f'(a)}\) は \(\large{y=f(x)}\) のグラフを描いたとき、\(\large{x=a}\) における接線の傾きを表します。

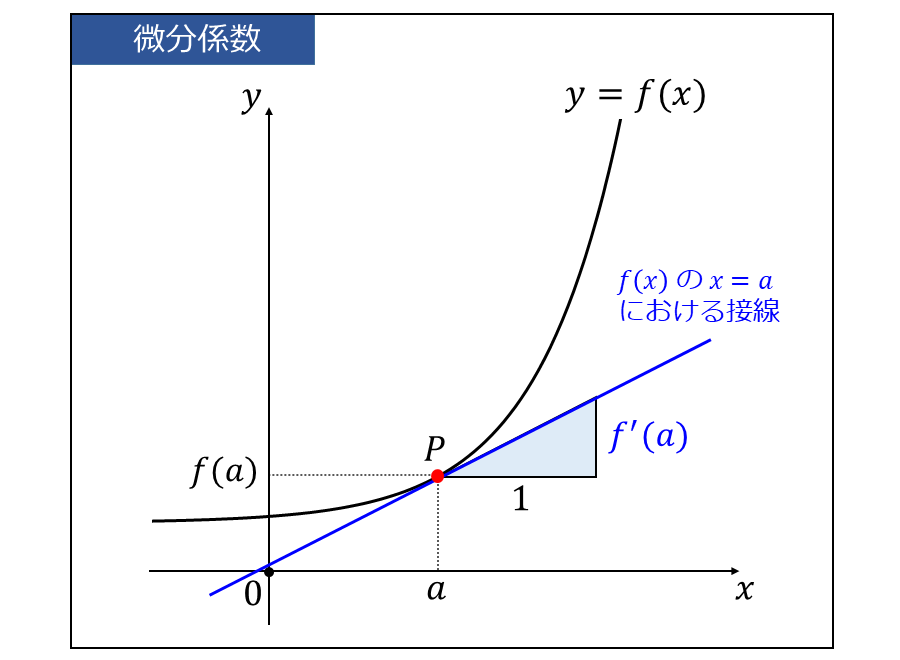
関数 \(\large{f(x)}\) の \(\large{x=a}\) における微分係数 \(\large{f'(a)}\) は、以下の式により求めることができます。

上記の微分係数の計算において \(\large{a}\) を \(\large{x}\) に置き換えると、関数\(\large{f(x)}\) の \(\large{x}\) における微分係数を表す関数が得られます。
関数\(\large{f(x)}\) の \(\large{x}\) における微分係数を表す関数を 導関数 といい、\(\large{f'(x)}\) により表します。

導関数\(\large{f'(x)}\) は、以下の式により定義されます。

・微分係数 と 導関数 の関係

導関数\(\large{f'(x)}\) とは、関数\(\large{f(x)}\) の \(\large{x}\) における微分係数を表したものです。
このとき、微分係数\(\large{f'(a)}\) は 導関数 \(\large{f'(x)}\) に \(\large{x=a}\) を代入することで得られます。

以下に、導関数 と 微分係数 の関係を利用する例題を解説します。

【例題】の解答
導関数の定義 $$\large{f'(x) = \lim_{h \to 0}\frac{f(x+h)-f(x)}{h}}$$ から、関数\(\large{f(x)=x^2}\) の導関数を求めると \begin{eqnarray} \large f'(x) &\large =&\large\lim_{h \to 0}\frac{(x+h)^2-x^2}{h}\\[0.5em] \large &\large =&\large \lim_{h \to 0}\frac{x^2+2xh+h^2-x^2}{h} \\[0.5em] \large &\large =&\large \lim_{h \to 0}\frac{2xh+h^2}{h} \\[0.5em] \large &\large =&\large \lim_{h \to 0}(2x+h) \\[0.5em] \large &\large =&\large 2x \\[0.5em] \end{eqnarray} したがって、関数\(\large{f(x)=x^2}\) の導関数は $$\large{f'(x)=2x}$$ となります。

ここで、導関数 \(\large{f'(x)=2x}\) に \(\large{x=1}\) を代入することで、\(\large{x=1}\) における微分係数が求められます。 $$\large{f'(1)=2\cdot1 = 2}$$ すなわち、
・関数\(\large{f(x)=x^2}\) の導関数は \(\large{f'(x)=2x}\)
・関数\(\large{f(x)=x^2}\) の \(\large{x=1}\) における微分係数は \(\large{2}\)
となります。

【2】問題と解き方

本章では、導関数の定義 に関連した問題について解説します。

(解答と解説 : 問題(1) 問題(2) 問題(3) 問題(4) 問題(5) 問題(6) 問題(7))

問題.1 定数関数の導関数

【解答と解説】
本問は、定数関数の導関数を求める問題です。

問題文の『導関数の定義に従って、以下の関数の導関数を求めよ』とは、以下の導関数の定義を利用することを意味します。

上記の導関数の定義から、定数関数 \(\large{f(x)=c}\) の導関数は、以下のように求められます。 \begin{eqnarray} \large f'(x) &\large =&\large\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}\\[0.5em] \large &\large =&\large\lim_{h \to 0}\frac{c-c}{h}\\[0.5em] \large &\large =&\large \lim_{h \to 0}\frac{0}{h} \\[0.5em] \large &\large =&\large 0 \\[0.5em] \end{eqnarray}

したがって、\(\displaystyle \large{f(x)=c}\) の導関数は \(\large{f'(x)=0}\) となります。

\(\large{f'(x)=0}\) は、変数\(\large{x}\) によってグラフの傾きが変化しないことを意味しています。

問題.2 二次関数の導関数

【解答と解説】
本問は、二次関数の導関数を定義に従って求める問題です。

導関数の定義 $$\large{f'(x) = \lim_{h \to 0}\frac{f(x+h)-f(x)}{h}}$$ から、 \begin{eqnarray} \large f'(x) &\large =&\large\lim_{h \to 0}\frac{2(x+h)^2-2x^2}{h}\\[0.5em] \large &\large =&\large \lim_{h \to 0}\frac{2(x^2+2xh+h^2)-2x^2}{h} \\[0.5em] \large &\large =&\large \lim_{h \to 0}\frac{4xh+2h^2}{h} \\[0.5em] \large &\large =&\large \lim_{h \to 0}(4x+2h) \\[0.5em] \large &\large =&\large 4x \\[0.5em] \end{eqnarray} となります。

したがって、\(\displaystyle \large{f(x)=2x^2}\) の導関数は \(\large{f'(x)=4x}\) となります。

問題.3 三次関数の導関数

【解答と解説】
本問は、三次関数の導関数を定義に従って求める問題です。

導関数の定義 $$\large{f'(x) = \lim_{h \to 0}\frac{f(x+h)-f(x)}{h}}$$ から、 \begin{eqnarray} \large f'(x) &\large =&\large\lim_{h \to 0}\frac{(x+h)^3-x^3}{h}\\[0.5em] \large &\large =&\large \lim_{h \to 0}\frac{(x^3+3x^2h+3xh^2+h^3)-x^3}{h} \\[0.5em] \large &\large =&\large \lim_{h \to 0}\frac{3x^2h+3xh^2+h^3}{h} \\[0.5em] \large &\large =&\large \lim_{h \to 0}(3x^2+3xh+h^2) \\[0.5em] \large &\large =&\large 3x^2 \\[0.5em] \end{eqnarray} となります。

したがって、\(\displaystyle \large{f(x)=x^3}\) の導関数は \(\large{f'(x)=3x^2}\) となります。

問題.4 分数関数の導関数

【解答と解説】
本問は、分数関数の導関数を定義に従って求める問題です。

導関数の定義 $$\large{f'(x) = \lim_{h \to 0}\frac{f(x+h)-f(x)}{h}}$$ から、 \begin{eqnarray} \large f'(x) &\large =&\large\lim_{h \to 0}\frac{1/(x+h)-1/x}{h}\\[0.5em] \large &\large =&\large \lim_{h \to 0}\frac{1}{h}\left(\frac{1}{x+h}-\frac{1}{x}\right)\\[0.5em] \large &\large =&\large \lim_{h \to 0}\frac{1}{h}\frac{x-(x+h)}{x(x+h)}\\[0.5em] \large &\large =&\large \lim_{h \to 0}\frac{1}{h}\frac{-h}{x(x+h)}\\[0.5em] \large &\large =&\large \lim_{h \to 0}\frac{-1}{x(x+h)}\\[0.5em] \large &\large =&\large -\frac{1}{x^2}\\[0.5em] \end{eqnarray} となります。

したがって、\(\displaystyle \large{f(x)=\frac{1}{x}}\) の導関数は \(\displaystyle\large{f'(x)=-\frac{1}{x^2}}\) となります。

問題.5 分数関数の導関数

【解答と解説】
本問は、分数関数の導関数を定義に従って求める問題です。

導関数の定義 $$\large{f'(x) = \lim_{h \to 0}\frac{f(x+h)-f(x)}{h}}$$ から、 \begin{eqnarray} \large f'(x) &\large =&\large\lim_{h \to 0}\frac{1/(2(x+h)+1)-1/(2x+1)}{h}\\[0.5em] \large &\large =&\large \lim_{h \to 0}\frac{1}{h}\left(\frac{1}{2(x+h)+1}-\frac{1}{2x+1}\right)\\[0.5em] \large &\large =&\large \lim_{h \to 0}\frac{1}{h}\frac{2x+1-\{2(x+h)+1\}}{(2x+2h+1)(2x+1)}\\[0.5em] \large &\large =&\large \lim_{h \to 0}\frac{1}{h}\frac{-2h}{(2x+2h+1)(2x+1)}\\[0.5em] \large &\large =&\large \lim_{h \to 0}\frac{-2}{(2x+2h+1)(2x+1)}\\[0.5em] \large &\large =&\large -\frac{2}{(2x+1)^2}\\[0.5em] \end{eqnarray} となります。

したがって、\(\displaystyle \large{f(x)=\frac{1}{2x+1}}\) の導関数は \(\displaystyle\large{f'(x)=-\frac{2}{(2x+1)^2}}\) となります。

問題.6 無理関数の導関数

【解答と解説】
本問は、無理関数の導関数を定義に従って求める問題です。

導関数の定義 $$\large{f'(x) = \lim_{h \to 0}\frac{f(x+h)-f(x)}{h}}$$ から、 \begin{eqnarray} \large f'(x) &\large =&\large\lim_{h \to 0}\frac{\sqrt{x+h}-\sqrt{x}}{h}\\[0.5em] \large &\large =&\large \lim_{h \to 0}\frac{1}{h}\frac{(\sqrt{x+h}-\sqrt{x})(\sqrt{x+h}+\sqrt{x})}{\sqrt{x+h}+\sqrt{x}}\\[0.5em] \large &\large =&\large \lim_{h \to 0}\frac{1}{h}\frac{(x+h)-x}{\sqrt{x+h}+\sqrt{x}}\\[0.5em] \large &\large =&\large \lim_{h \to 0}\frac{1}{h}\frac{h}{\sqrt{x+h}+\sqrt{x}}\\[0.5em] \large &\large =&\large \lim_{h \to 0}\frac{1}{\sqrt{x+h}+\sqrt{x}}\\[0.5em] \large &\large =&\large \frac{1}{2\sqrt{x}}\\[0.5em] \end{eqnarray} となります。

したがって、\(\displaystyle \large{f(x)=\sqrt{x}}\) の導関数は \(\displaystyle\large{f'(x)= \frac{1}{2\sqrt{x}}}\) となります。

問題.7 無理関数の導関数

【解答と解説】
本問は、無理関数の導関数を定義に従って求める問題です。

導関数の定義 $$\large{f'(x) = \lim_{h \to 0}\frac{f(x+h)-f(x)}{h}}$$ から、 \begin{eqnarray} \large f'(x) &\large =&\large\lim_{h \to 0}\frac{1/\sqrt{3(x+h)}-1/\sqrt{3x}}{h}\\[0.5em] \large &\large =&\large \lim_{h \to 0}\frac{1}{h}\left(\frac{1}{\sqrt{3(x+h)}}-\frac{1}{\sqrt{3x}}\right)\\[0.5em] \large &\large =&\large \lim_{h \to 0}\frac{1}{h}\left(\frac{\sqrt{3x}-\sqrt{3(x+h)}}{\sqrt{3(x+h)}\cdot\sqrt{3x}}\right)\\[0.5em] \large &\large =&\large \lim_{h \to 0}\frac{1}{\sqrt{3}h}\left(\frac{\sqrt{x}-\sqrt{x+h}}{\sqrt{x+h}\cdot\sqrt{x}}\right)\\[0.5em] \large &\large =&\large \lim_{h \to 0}\frac{1}{\sqrt{3}h}\frac{x-(x+h)}{\sqrt{x(x+h)}(\sqrt{x}+\sqrt{x+h})}\\[0.5em] \large &\large =&\large \lim_{h \to 0}\frac{1}{\sqrt{3}h}\frac{-h}{\sqrt{x(x+h)}(\sqrt{x}+\sqrt{x+h})}\\[0.5em] \large &\large =&\large \lim_{h \to 0}\frac{-1}{\sqrt{3}\sqrt{x(x+h)}(\sqrt{x}+\sqrt{x+h})}\\[0.5em] \large &\large =&\large -\frac{1}{2\sqrt{3}}x^{-\frac{3}{2}}\\[0.5em] \end{eqnarray} となります。

したがって、\(\displaystyle \large{f(x)=\frac{1}{\sqrt{3x}}}\) の導関数は \(\displaystyle\large{-\frac{1}{2\sqrt{3}}x^{-\frac{3}{2}}}\) となります。

---