関数の極限
本項では以下の内容を解説します。
- ・関数の極限の性質
- ・極限の発散
- ・右側極限と左側極限
- ・問題と解き方
【1】関数の極限
関数の極限とは、関数\(\large{f(x)}\) において 変数\(\large{x}\)を ある値\(\large{a}\) と異なる値にとりながら \(\large{a}\) に限りなく近づける操作のことをいいます。
関数の極限を表記するときは、関数\(\large{f(x)}\) において \(\large{x}\) が \(\large{a}\) に限りなく近づくとき、関数\(\large{f(x)}\)がある一定の値 \(\large{\alpha}\) に近づくならば
$$\large{\lim_{x \to a}f(x) = \alpha}$$
と書きます。この \(\large{\alpha}\) を \(\large{x \to a}\) のときの関数\(\large{f(x)}\) の極限値といいます。
また、このとき 関数\(\large{f(x)}\) は、\(\large{\alpha}\) に収束するといいます。
【1-1】極限値の性質
関数の極限値には、以下のような性質があります。
\begin{eqnarray} &&\large \cdot\hspace{2pt}\lim_{x \to a}f(x) + \lim_{x \to a}g(x)= \alpha + \beta\\[0.7em] &&\large \cdot\hspace{2pt} c\lim_{x \to a}f(x) =\large c\hspace{1pt}\alpha\\[0.7em] &&\large \cdot\hspace{2pt}\lim_{x \to a}f(x)\hspace{1pt}g(x) =\alpha\hspace{1pt}\beta\\[0.7em] &&\large \cdot\hspace{2pt}\frac{\lim_{x \to a}f(x)}{\lim_{x \to a}g(x)}=\frac{\alpha}{\beta} \\ \end{eqnarray} (ただし、\(\large{c}\) は定数、\(\large{\beta \neq 0}\))
以下に極限値の性質を利用した例題を解説します。
\(\displaystyle \large{(1)\hspace{5pt}\lim_{x \to 1}(2x^3+3x)}\)
\(\displaystyle \large{(2)\hspace{5pt}\lim_{x \to 2}\frac{x^2}{x-1}\hspace{15pt}}\)
\(\large{x}\)の多項式や分数関数、三角関数、指数関数、対数関数などの関数では、\(\large{a}\) が \(\large{x}\) の定義域に含まれる場合 $$\large{\lim_{x \to a}f(x) = f(a)}$$ と極限値を求めることができます。
例題1(1)は、各項の極限値を求めてから、足し合わせればよいので \begin{eqnarray} \large \lim_{x \to 1}(2x^3+3x)&\large= &\large 2\cdot 1^3+3\cdot1\\[0.5em] \large & \large=&\large 5\\[0.7em] \end{eqnarray} となります。
例題1(2)は、分母と分子の極限値を求めてから、分数を計算すればよいため $$\large{\lim_{x \to 2}\frac{x^2}{x-1} = \frac{2^2}{2-1}= 4}$$ となります。
【1-2】極限が発散する場合
関数 \(\large{f(x)}\) において \(\large{x}\) が \(\large{a}\) と異なる値をとりながら \(\large{a}\) に限りなく近づくとき、関数\(\large{f(x)}\) が正に限りなく大きくなるとき $$\large{\lim_{x \to a}f(x) = \infty}$$ と書きます。
また、関数\(\large{f(x)}\) が負に限りなく大きくなるときは $$\large{\lim_{x \to a}f(x) = -\infty}$$ と書きます。
関数の極限が正に限りなく大きくなるとき、正の無限大に発散するといいます。また、負に限りなく大きくなるとき、負の無限大に発散するといいます。
\(\displaystyle \large{\lim_{x \to 1}\frac{2}{(x-1)^2}}\)
関数 \(\displaystyle\large{f(x)=\frac{2}{(x-1)^2}}\) は下図のように \(\large{x=1}\) で正に限りなく大きなる関数です。
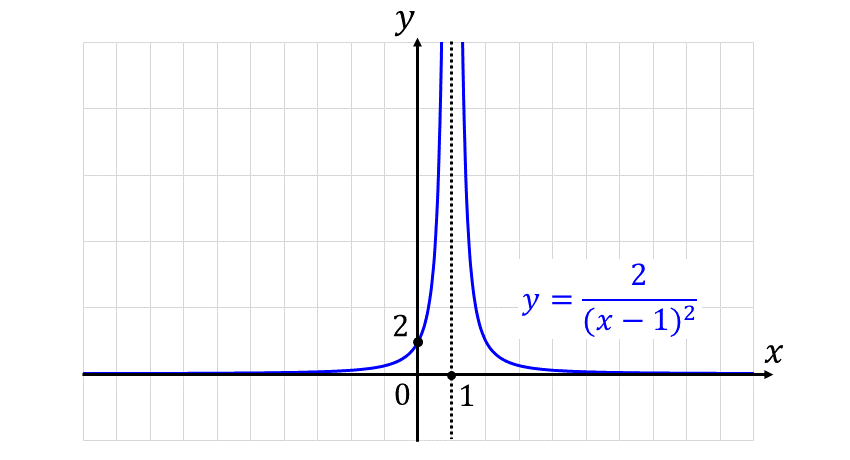
関数 \(\large{f(x)}\) が正に限りなく大きくなることから $$\large{\lim_{x \to 1}\frac{2}{(x-1)^2} = \infty}$$ となります。
【1-3】右側極限と左側極限
関数 \(\large{f(x)}\) において \(\large{x}\) が \(\large{a}\) より大きい値をとりながら \(\large{a}\) に限りなく近づくときの極限を右側極限といい、以下のように表記します。 $$\large{\lim_{x \to a+0}f(x) = \alpha}$$
一方、\(\large{x}\) が \(\large{a}\) より小さい値をとりながら \(\large{a}\) に限りなく近づくときの極限を左側極限といい、以下のように表記します。 $$\large{\lim_{x \to a-0}f(x) = \alpha}$$
関数 \(\large{f(x)}\) における \(\large{x \to a}\) の極限 \(\hspace{1pt}\displaystyle\large{\lim_{x \to a}f(x)}\hspace{1pt}\)が存在するとき、右側極限と左側極限は一致するため、以下の式が成り立ちます。 $$\large{\lim_{x \to a+0}f(x) = \lim_{x \to a-0}f(x)}$$
\(\displaystyle \large{f(x) = \frac{1}{x-2}}\)
関数 \(\displaystyle \large{f(x) = \frac{1}{x-2}}\) をグラフにすると以下のようになります。
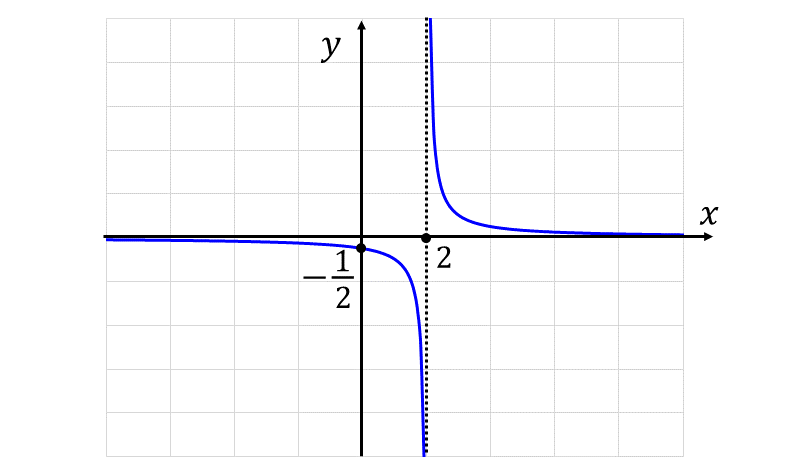
\(\large{x=2}\) における右側極限を求めると $$\large{\lim_{x \to 2+0}\frac{1}{x-2}= \infty}$$ \(\large{x=2}\) における左側極限を求めると $$\large{\lim_{x \to 2-0}\frac{1}{x-2}= -\infty}$$ となります。
上記のような、右側極限と左側極限が一致しない場合、\(\large{x \to 2}\) のときの 関数 \(\large{f(x)}\) の極限は存在しません。
【2】問題と解き方
本章では、関数の極限 に関連した問題について解説します。
\(\displaystyle \large{\lim_{x \to 1}\frac{x-1}{x^2-1}}\)
\(\displaystyle \large{\lim_{x \to 3}\frac{x^2-5x+6}{x^2-4x+3}}\)
問題1、問題2 は 因数分解を利用する問題です。
(解答と解説 : 問題1 問題2)
\(\displaystyle \large{\lim_{x \to 2}\frac{x-2}{\sqrt{2x}-2}}\)
\(\displaystyle \large{\lim_{x \to 1}\frac{\sqrt{x+3}-2}{x-1}}\)
問題3、問題4 は 有理化を利用する問題です。
(解答と解説 : 問題3 問題4)
\(\displaystyle \large{\lim_{x \to \infty}\frac{x^2+3}{3x^2+4x+2}}\)
問題5 は \(\large{x \to \infty}\) の場合の問題です。
(解答と解説 : 問題5)
\(\displaystyle\large{\lim_{x \to 1}f(x)}\) が存在するか調べよ
\(\displaystyle \large{f(x) = \frac{x^2-1}{|x-1|}}\)
問題6 は 右側極限と左側極限を計算し、極限が存在するか調べる問題です。
(解答と解説 : 問題6)
\(\displaystyle \large{\lim_{x \to 1}\frac{ax+b}{\sqrt{x}-1}=2}\)
問題7 は 極限値から関数の定数を決定する問題です。
(解答と解説 : 問題7)
問題.1 因数分解を利用する問題
\(\displaystyle \large{\lim_{x \to 1}\frac{x-1}{x^2-1}}\)
問題の関数をそのまま \(\large{x \to 1}\) の極限をとろうとすると、\(\displaystyle\large{\frac{0}{0}}\) となり極限値を求めることができません。
このように関数の極限が \(\displaystyle\large{\frac{0}{0}}\)、\(\displaystyle\large{\frac{\infty}{\infty}}\)、\(\displaystyle\large{\infty-\infty}\) となる場合を不定形といい、極限値を求めることができません。
本問では、因数分解により式を変形し、不定形を解消して極限値を求めます。 \begin{eqnarray} \large \lim_{x \to 1}\frac{x-1}{x^2-1}&\large =&\large \lim_{x \to 1}\frac{x-1}{(x+1)(x-1)} \\[0.5em] \large &\large =&\large \lim_{x \to 1}\frac{1}{x+1} \\ \large &\large =&\large \frac{1}{2} \\ \end{eqnarray}
問題.2 因数分解を利用する問題
\(\displaystyle \large{\lim_{x \to 3}\frac{x^2-5x+6}{x^2-4x+3}}\)
問題1と同様に、問題の関数をそのまま \(\large{x \to 3}\) の極限をとろうとすると、\(\displaystyle\large{\frac{0}{0}}\) となり極限値を求めることができません。
そのため、分母と分子を因数分解して式変形します。
\begin{eqnarray}
\large
\lim_{x \to 3}\frac{x^2-5x+6}{x^2-4x+3}&\large =&\large \lim_{x \to 3}\frac{(x-2)(x-3)}{(x-1)(x-3)} \\[0.5em]
\large
&\large =&\large \lim_{x \to 3}\frac{x-2}{x-1} \\[0.5em]
\large
&\large =&\large \frac{1}{2} \\
\end{eqnarray}
問題.3 有理化を利用する問題
\(\displaystyle \large{\lim_{x \to 2}\frac{x-2}{\sqrt{2x}-2}}\)
問題1、問題2 と同様に、問題の関数をそのまま \(\large{x \to 2}\) の極限をとると、\(\displaystyle\large{\frac{0}{0}}\) となり極限値を求めることができません。
本問のように、分子もしくは分母に ルート が含まれている場合は、有理化により式変形をします。
問題の関数の分母、分子に \(\large{\sqrt{2x}+2}\) をかけると \begin{eqnarray} \large \lim_{x \to 2}\frac{x-2}{\sqrt{2x}-2}&\large =&\large \lim_{x \to 2}\frac{(x-2)(\sqrt{2x}+2)}{(\sqrt{2x}-2)(\sqrt{2x}+2)} \\[0.5em] \large &\large =&\large \lim_{x \to 2}\frac{(x-2)(\sqrt{2x}+2)}{2x-4} \\[0.5em] \large &\large =&\large \lim_{x \to 2}\frac{(x-2)(\sqrt{2x}+2)}{2(x-2)} \\[0.5em] \large &\large =&\large \lim_{x \to 2}\frac{\sqrt{2x}+2}{2} \\[0.5em] \large &\large =&\large 2 \\[0.5em] \end {eqnarray}
問題.4 有理化を利用する問題
\(\displaystyle \large{\lim_{x \to 1}\frac{\sqrt{x+3}-2}{x-1}}\)
問題3 と同様に、分子もしくは分母に ルート が含まれているため、有理化により式変形をします。
問題の関数の分母、分子に \(\large{\sqrt{x+3}+2}\) をかけると \begin{eqnarray} \large \lim_{x \to 1}\frac{\sqrt{x+3}-2}{x-1}&\large =&\large \lim_{x \to 1}\frac{(\sqrt{x+3}-2)(\sqrt{x+3}+2)}{(x-1)(\sqrt{x+3}+2)} \\[0.5em] \large &\large =&\large\lim_{x \to 1}\frac{x+3 - 4}{(x-1)(\sqrt{x+3}+2)} \\[0.5em] \large &\large =&\large \lim_{x \to 1}\frac{x-1}{(x-1)(\sqrt{x+3}+2)} \\[0.5em] \large &\large =&\large \lim_{x \to 1}\frac{1}{\sqrt{x+3}+2} \\[0.5em] \large &\large =&\large \frac{1}{4} \\[0.5em] \end {eqnarray}
問題.5 x→∞ の極限の問題
\(\displaystyle \large{\lim_{x \to \infty}\frac{x^2+3}{3x^2+4x+2}}\)
本問は、\(\large{x \to \infty}\) の極限値を求めると、\(\displaystyle\large{\frac{\infty}{\infty}}\) の不定形となってしまいます。
そこで、以下のように関数 \(\displaystyle\large{\frac{1}{x}}\) や \(\displaystyle\large{\frac{1}{x^2}}\) が \(\displaystyle\large{x \to \infty}\) のときに限りなく \(\large{0}\) に近づくことを利用して極限値を求めます。 $$\large{\lim_{x \to \infty}\frac{1}{x}=0\hspace{1pt},\hspace{3pt}\lim_{x \to \infty}\frac{1}{x^2}=0}$$
問題の式を変形すると、 $$\large{\lim_{x \to \infty}\frac{x^2+3}{3x^2+4x+2} = \lim_{x \to \infty}\frac{1+\frac{3}{x^2}}{3+\frac{4}{x}+\frac{2}{x^2}}}$$ ここで、\(\displaystyle\large{\lim_{x \to \infty}\frac{1}{x}=0\hspace{1pt},\hspace{3pt}\lim_{x \to \infty}\frac{1}{x^2}=0}\) より、 $$\large{\lim_{x \to \infty}\frac{1+\frac{3}{x^2}}{3+\frac{4}{x}+\frac{2}{x^2}} = \frac{1}{3}}$$ と求められます。
問題.6 右側極限と左側極限の問題
\(\displaystyle\large{\lim_{x \to 1}f(x)}\) が存在するか調べよ
\(\displaystyle \large{f(x) = \frac{x^2-1}{|x-1|}}\)
本問は、右側極限と左側極限 を計算し、極限が存在するかを調べる問題です。
関数 \(\large{f(x)}\) の右側極限は、
\(\large{x \to 1+0}\) のとき \(\large{x>1}\) より \(\large{|x-1|=x-1}\) であることから、
\begin{eqnarray}
\large
\lim_{x \to 1+0} \frac{x^2-1}{|x-1|}&\large =&\large \lim_{x \to 1+0}\frac{x^2-1}{x-1} \\[0.5em]
\large
&\large =&\large \lim_{x \to 1+0}\frac{(x+1)(x-1)}{x-1} \\[0.5em]
\large
&\large =&\large \lim_{x \to 1+0}(x+1) \\[0.5em]
\large
&\large =&\large 2 \\[0.5em]
\end{eqnarray}
となります。
また、関数 \(\large{f(x)}\) の左側極限は、
\(\large{x \to 1-0}\) のとき \(\large{x < 1}\) より \(\large{|x-1|=-x+1}\) であることから、
\begin{eqnarray}
\large
\lim_{x \to 1-0} \frac{x^2-1}{|x-1|}&\large =&\large \lim_{x \to 1-0}\frac{x^2-1}{-x+1} \\[0.5em]
\large
&\large =&\large \lim_{x \to 1-0}\frac{(x+1)(x-1)}{-(x-1)} \\[0.5em]
\large
&\large =&\large \lim_{x \to 1-0}(-(x+1)) \\[0.5em]
\large
&\large =&\large -2 \\[0.5em]
\end{eqnarray}
となります。
したがって、関数\(\large{f(x)}\) の右側極限と左側極限は一致しないことから、\(\displaystyle\large{\lim_{x \to 1}f(x)}\) は存在しません。
問題.7 極限値から定数を決定する問題
\(\displaystyle \large{\lim_{x \to 1}\frac{ax+b}{\sqrt{x}-1}=2}\)
問題の分母は、 $$\large{\lim_{x \to 1}(\sqrt{x}-1)=0}$$ となります。
ここで、分子の極限について考えると、極限値の性質から \begin{eqnarray} \large \lim_{x \to 1}(ax+b)&\large =&\large \lim_{x \to 1}\frac{ax+b}{\sqrt{x}-1}\cdot(\sqrt{x}-1) \\[0.5em] \large &\large =&\large 2 \cdot 0 \\[0.5em] \large &\large =&\large 0\\[0.5em] \end{eqnarray} が成り立ちます。
したがって、 $$\large{\lim_{x \to 1}(ax+b) = 0}$$ であるため $$\large{b=-a}$$ が導かれます。
問題の式に代入して式変形すると、 \begin{eqnarray} \large \lim_{x \to 1}\frac{ax+b}{\sqrt{x}-1}&\large =&\large \lim_{x \to 1}\frac{a(x-1)}{\sqrt{x}-1} \\[0.5em] \large &\large =&\large \lim_{x \to 1}\frac{a(x-1)(\sqrt{x}+1)}{(\sqrt{x}-1)(\sqrt{x}+1)}\\[0.5em] \large &\large =&\large \lim_{x \to 1}\frac{a(x-1)(\sqrt{x}+1)}{x-1}\\[0.5em] \large &\large =&\large \lim_{x \to 1}a(\sqrt{x}+1)\\[0.5em] \large &\large =&\large 2a\\[0.5em] \end{eqnarray}
上記の極限値が \(\large{2}\) に一致すればよいので $$\large{2a = 2}$$ から $$\large{a = 1}$$ となります。
したがって、求める定数は \(\large{a=1\hspace{1pt},b=-1}\) となります。