-光と光学に関連する用語の解説サイト-

関数の連続と微分可能性

本項では、『関数の連続』と『微分可能性』や問題の解き方について解説します。

1. 関数の連続
- ・例題1
2. 微分可能性
- ・例題2
3. 問題と解き方
- ・問題1
- ・問題2

【1】関数の連続

関数が連続であるとは、『関数のグラフが切れずにつながっている』ことを表します。

関数 $\large{f(x)}$ が $\large{x=a}$ で連続であるとき、以下が成り立ちます。

【関数の連続】

関数 $\large{y=f(x)}$ が $\large{x=a}$ で連続であるとき
$\displaystyle\large{\lim_{x \to a}f(a)}$ が存在し、その値が $\large{f(a)}$ に等しい

定義域のすべての点で連続である関数を連続関数といいます。
例えば、$\large{y=x}$ や $\large{y=\sin x}$ などは連続関数です。

また、$\large{x=a}$ で関数が連続していなければ、『$\large{\boldsymbol{x=a}}$ で不連続』といいます。

・例題1

【例題1】

関数 $\displaystyle \large{f(x)=|x|}$ は $\large{x=0}$ において連続か調べよ

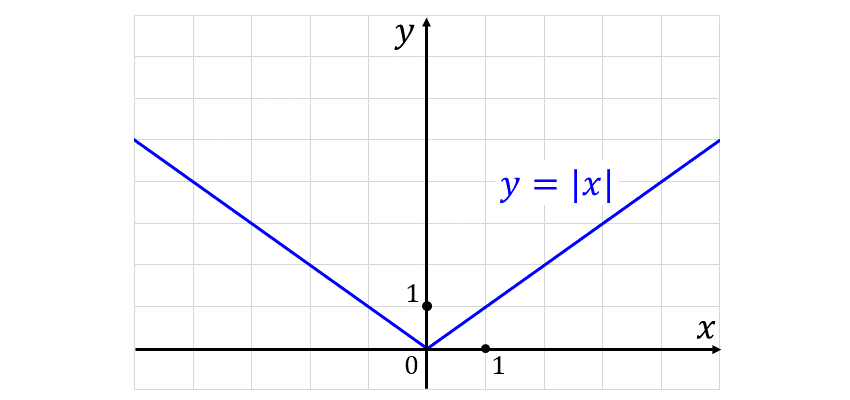
関数 $\displaystyle \large{f(x)=|x|}$ は、以下のようなグラフの形状をしています。 $関数y=|x|の連続性を調べる問題$

上図の関数 $\displaystyle \large{f(x)=|x|}$ は $\large{x=0}$ において連続かを調べます。

右側極限は $$\large{\lim_{x \to +0} |x| = \lim_{x \to +0} x =0}$$ 左側極限は $$\large{\lim_{x \to -0} |x| = \lim_{x \to -0} (-x) =0}$$ したがって、$\displaystyle\large{\lim_{x \to 0} |x| = 0}$ となります。

また、$\large{f(0)=0}$ であるため $$\large{\lim_{x \to 0} |x| = f(0)}$$ が成り立つことから、関数 $\large{f(x) = |x|}$ は $\large{x=0}$ において連続する関数です。

【2】微分可能性

関数が微分可能であるとは、『関数のグラフが滑らかにつながっている』ことを表します。

関数 $\large{f(x)}$ が $\large{x=a}$ で微分可能であるとき、以下が成り立ちます。

【関数の微分可能性】

関数 $\large{y=f(x)}$ が $\large{x=a}$ で微分可能であるとき
$\displaystyle\large{f'(a) = \lim_{h \to 0}\frac{f(a+h)-f(a)}{h}}$ が存在する

関数 $\large{f(x)}$ が $\large{x=a}$ で微分係数が存在するとき、『関数$\large{f(x)}$は $\large{x=a}$ で微分可能』といいます。

関数の連続と微分可能性の関係

関数の連続と微分可能性には、以下のような関係があります。

【関数の連続と微分可能性】

関数 $\large{y=f(x)}$ が $\large{x=a}$ で微分可能ならば
$\displaystyle\large{x=a}$ で連続である

一方、『関数 $\large{y=f(x)}$ が $\large{x=a}$ で連続であっても、$\displaystyle\large{x=a}$ で微分可能とは限らない』という点に注意が必要です。

例題2

【例題】

関数 $\displaystyle \large{f(x)=|x|}$ の $\large{x=0}$ において微分可能かを調べよ

【解答と解説】
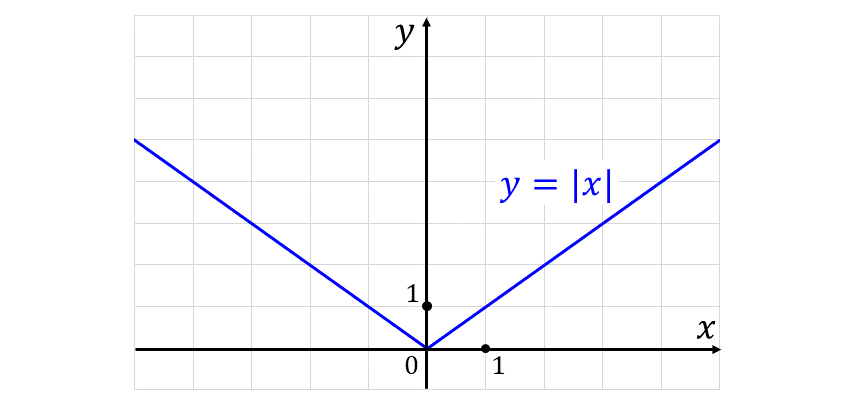
関数 $\displaystyle \large{f(x)=|x|}$ は、以下のようなグラフの形状をしています。 $y=|x|の微分可能性の計算問題$

例題1で調べたように、関数 $\displaystyle \large{f(x)=|x|}$ は $$\large{\lim_{h \to a}f(a) = f(0)=0}$$ であるため、$\large{x=0}$ において連続する関数です。

関数 $\displaystyle \large{f(x)=|x|}$ が $\large{x=0}$ で微分可能かを調べるため、右微分係数$\large{f'_+(0)}$ と左微分係数$\large{f'_-(0)}$ を求めます。

$\large{x=0}$ における右微分係数を求めると \begin{eqnarray} \large f'_+(0) &\large =&\large\lim_{h \to +0}\frac{f(0+h)-f(0)}{h}\\[0.5em] \large &\large =&\large \lim_{h \to +0}\frac{|h|}{h} \\[0.5em] \large &\large =&\large \lim_{h \to +0}\frac{h}{h} \\[0.5em] \large &\large =&\large 1 \\[0.5em] \end{eqnarray} となります。

一方、$\large{x=0}$ における左微分係数を求めると \begin{eqnarray} \large f'_-(0) &\large =&\large\lim_{h \to -0}\frac{f(0+h)-f(0)}{h}\\[0.5em] \large &\large =&\large \lim_{h \to -0}\frac{|h|}{h} \\[0.5em] \large &\large =&\large \lim_{h \to -0}\frac{-h}{h} \\[0.5em] \large &\large =&\large -1 \\[0.5em] \end{eqnarray} となります。

したがって、右微分係数$\large{f'_+(0)}$ と左微分係数$\large{f'_-(0)}$ が一致しないため、関数 $\large{y=|x|}$ は $\large{x=0}$ において微分可能ではないことが分かります。

【3】問題と解き方

本章では、関数の連続と微分可能性に関連した問題について解説します。

問題.1

関数 $\displaystyle \large{f(x)=|x|(x-1)}$ の $\large{x=0}$ において
関数が連続か、微分可能かを調べよ

問題1 は、関数の連続と微分可能性を調べる問題です。
(解答と解説 : 問題1)

問題.2

関数 $\displaystyle \large{f(x)=x^2+ax+b}$ $\large{(x \geqq 0)}$ と関数$\displaystyle \large{f(x)=\sin x}$ $\large{(x < 0)}$ が $\large{x=0}$ において微分可能であるとき、定数$\large{a,b}$ を求めよ。

問題2 は、微分可能性の条件から、関数の定数を決定する問題です。
(解答と解説 : 問題2)

問題.1 微分可能性の問題

問題.1

関数 $\displaystyle \large{f(x)=|x|(x-1)}$ の $\large{x=0}$ において
関数が連続か、微分可能かを調べよ

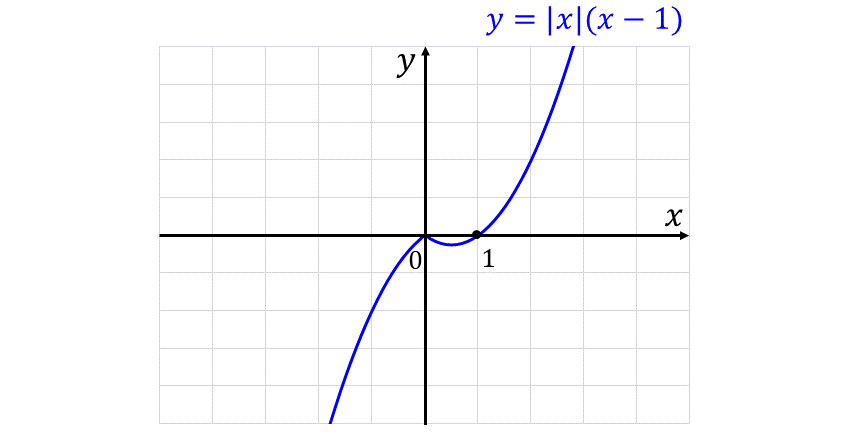
関数 $\displaystyle \large{f(x)=|x|(x-1)}$ は、以下のようなグラフの形状をしています。 $y=|x|(x-1)の微分可能性の計算問題$

まず、関数 $\displaystyle \large{f(x)=|x|(x-1)}$ は $\large{x=0}$ において連続かを調べます。

右側極限は $$\large{\lim_{x \to +0} |x|(x-1) = \lim_{x \to +0} x(x-1) =0}$$ 左側極限は $$\large{\lim_{x \to -0} |x|(x-1) = \lim_{x \to -0} -x(x-1) =0}$$ であるため、極限 $\displaystyle\large{\lim_{x \to 0} |x|(x-1) = 0}$ となります。

$\large{f(0)=0}$ であるため、 $$\large{\lim_{x \to 0} |x|(x-1) = f(0)}$$ が成り立つため、関数 $\large{f(x) = |x|(x-1)}$ は $\large{x=0}$ において連続する関数です。

次に、微分可能性について調べます。
$\large{x=0}$ における右微分係数を求めると \begin{eqnarray} \large f'_+(0) &\large =&\large\lim_{h \to +0}\frac{f(0+h)-f(0)}{h}\\[0.5em] \large &\large =&\large \lim_{h \to +0}\frac{|h|(h-1)}{h} \\[0.5em] \large &\large =&\large \lim_{h \to +0}\frac{h(h-1)}{h} \\[0.5em] \large &\large =&\large \lim_{h \to +0}(h-1) \\[0.5em] \large &\large =&\large -1 \\[0.5em] \end{eqnarray} となります。

一方、$\large{x=0}$ における左微分係数を求めると \begin{eqnarray} \large f'_-(0) &\large =&\large\lim_{h \to -0}\frac{f(0+h)-f(0)}{h}\\[0.5em] \large &\large =&\large \lim_{h \to -0}\frac{|h|(h-1)}{h} \\[0.5em] \large &\large =&\large \lim_{h \to -0}\frac{-h(h-1)}{h} \\[0.5em] \large &\large =&\large \lim_{h \to -0}(-h+1) \\[0.5em] \large &\large =&\large 1 \\[0.5em] \end{eqnarray} となります。

したがって、右微分係数は $\large{f'_+(0)=-1}$、左微分係数は $\large{f'_-(0)=1}$ であり一致しないため、関数 $\large{y=|x|(x-1)}$ は $\large{x=0}$ において微分可能ではないことが分かります。

問題.2 微分可能性から定数を決定する問題

問題.2

【解答と解説】
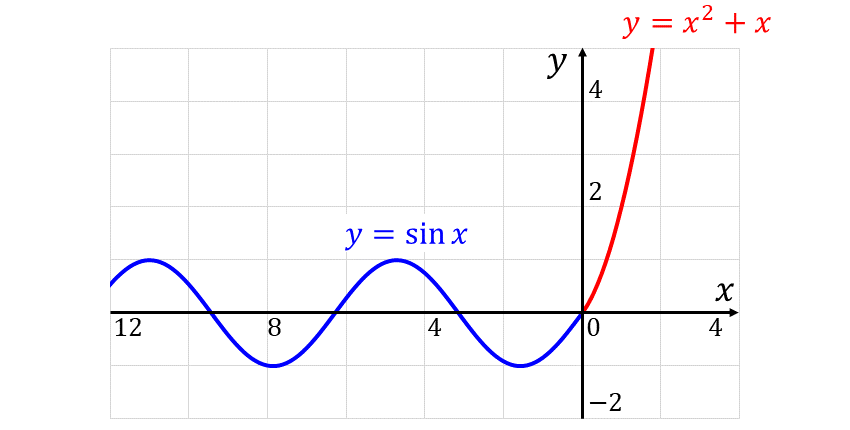
まず、関数 $\large{f(x)=x^2+ax+b}$ と関数 $\large{f(x)=\sin x}$ が $\large{x=0}$ で連続であるとき、 $$\large{\lim_{x \to +0} f(x)} = \large{\lim_{x \to -0} f(0)} = f(0)$$ が成り立ちます。

$$\large{\lim_{x \to +0} f(x) =\lim_{x \to +0} (x^2+ax+b) = b}$$ $$\large{\lim_{x \to -0} f(x) = \lim_{x \to +0} (\sin x) =0}$$ であることから、 $$\large{b=0}$$ となります。

次に、$\large{x=0}$ において微分可能であるとき、右微分係数$\large{f'_+(0)}$ と左微分係数$\large{f'_-(0)}$ が一致することを利用して定数を求めます。

$\large{x=0}$ における右微分係数を求めると \begin{eqnarray} \large f'_+(0) &\large =&\large\lim_{h \to +0}\frac{f(0+h)-f(0)}{h}\\[0.5em] \large &\large =&\large \lim_{h \to +0}\frac{h^2 + ah}{h} \\[0.5em] \large &\large =&\large \lim_{h \to +0}(h+a) \\[0.5em] \large &\large =&\large a \\[0.5em] \end{eqnarray} となります。

一方、$\large{x=0}$ における左微分係数を求めると \begin{eqnarray} \large f'_-(0) &\large =&\large\lim_{h \to -0}\frac{f(0+h)-f(0)}{h}\\[0.5em] \large &\large =&\large \lim_{h \to -0}\frac{\sin h}{h} \\[0.5em] \large &\large =&\large 1 \\[0.5em] \end{eqnarray} となります。

(計算過程で三角関数の極限 $\large{\displaystyle\lim_{x \to 0} \frac{\sin x}{x} = 1}$ を利用しています。)

したがって、関数$\large{f(x)}$ の右微分係数$\large{f'_+(0)}$ と左微分係数 $\large{f'_-(0)}$ が一致するとき、 $$\large{a=1}$$ となります。

よって、求める定数は $\large{a=1\hspace{1pt},\hspace{3pt}b=0}$ となります。

求められた定数を使用した関数 $\large{f(x)=x^2+x}$ $\large{(x \geqq 0)}$ と関数 $\large{f(x)=\sin x}$ $\large{(x < 0)}$ のグラフを描くと以下のようになります。 $関数と微分可能性と連続の条件から定数を決定する問題$