二次方程式の判別式の使い方

【1】二次方程式の判別式とは

判別式とは、二次方程式 \(\large{ax^2 +bx+c=0}\) の解の公式といわれる以下の式 $$\large{x = \frac{-b \pm \sqrt{\color{red}{b^2 -4ac}\color{black}{}}}{2a}}$$ に表れる \(\large{b^2 -4ac}\) の符号を利用して、『二次方程式の解の個数』や、『二次関数と\(\large{\boldsymbol{x}}\)軸の位置関係』を判別する式のことです。

判別式\(\large{D}\) は以下の式により定義されます。

・判別式D/4の計算

また、二次方程式の \(\large{x}\) の係数 \(\large{b}\) が偶数 (\(\large{b=2b'}\)) であるとき、 $$\large{D=4b'^2-4ac}$$ となります。したがって、判別式は \(\large{\frac{D}{4}=b'^2-ac}\) を求めればよく、計算が簡単になります。

・二次方程式の実数解の個数

判別式の符号は、二次方程式 \(\large{ax^2 +bx+c=0}\) の実数解の個数に対応しています。

『判別式\(\large{D}\)の符号』と『二次方程式の解の個数』の関係は、解の公式を調べることで分かります。

解の公式は以下の式により表されます。 $$\large{x = \frac{-b \pm \sqrt{\color{blue}{b^2 -4ac}\color{black}{}}}{2a}=\frac{-b \pm \sqrt{\color{blue}{D}\color{black}{}}}{2a}}$$ 上式から \(\large{D>0}\) であるとき、2つの異なる実数解を持つことが分かります。
また、\(\large{D=0}\) であれば、\(\large{\displaystyle x=\frac{-b \pm \sqrt{\color{blue}{D}\color{black}{}}}{2a}= -\frac{b}{2a}}\)より、1つの解のみを持つことが分かります。

\(\large{D < 0}\) のときは、解の公式の根号の中が負となってしまいます。したがって、\(\large{x}\) は実数の範囲に解を持たないため、実数解の個数は \(\large{0}\)個になります。

(二次方程式の判別式に関連する問題は後述しています。問題(1)～(2))

【2】二次関数のグラフと判別式

"二次方程式の実数解の個数" は、"二次関数のグラフが \(\large{\boldsymbol{x}}\)軸と交わる交点の数" と対応しています。
以下の表に、判別式\(\large{D}\) の符号と、\(\large{x}\)軸の交点の数を一覧で示します。

【2-1】判別式 D>0 の場合のグラフ

二次関数 \(\large{y=ax^2+bx+c}\) を平方完成した式は以下のように表されます。 $$\large{y=a \left(x + \frac{b}{2a}\right)^2 - \frac{b^2 -4ac}{4a}}$$

このとき、二次関数の頂点の \(\large{y}\)座標は、判別式\(\large{\color{blue}{D}}\) を使用して以下の式で表されます。 $$\large{- \frac{b^2 -4ac}{4a}=- \frac{\color{blue}{D}\color{black}{}}{4a}}$$

例えば、下図に二次関数 \(\large{y=ax^2+bx+c}\) の \(\large{x^2}\) の係数が \(\large{a>0}\)、判別式が \(\large{D > 0 }\) である場合のグラフを示します。

\(\large{a>0}\) かつ \(\large{D > 0 }\) のとき、二次関数の頂点の\(\large{y}\)座標は負となるため、\(\large{x}\)軸と異なる2点で交わることが分かります。

このとき、交点の\(\large{x}\)座標は解の公式から与えられる以下の値となります。 $$\large{x =\frac{-b \pm \sqrt{\color{blue}{D}\color{black}{}}}{2a}}$$

【2-2】判別式 D=0 の場合のグラフ

同様に、判別式が\(\large{D = 0 }\) のとき、二次関数の頂点の\(\large{y}\)座標は $$\large{- \frac{\color{blue}{D}\color{black}{}}{4a}=0}$$ であるため、二次関数のグラフは\(\large{x}\)軸と1点で接することが分かります。

このとき、交点の\(\large{x}\)座標は解の公式から与えられる以下の値となります。 $$\large{x =\frac{-b \pm \sqrt{\color{blue}{D}\color{black}{}}}{2a}=-\frac{b}{2a}}$$

【2-3】判別式 D < 0の場合のグラフ

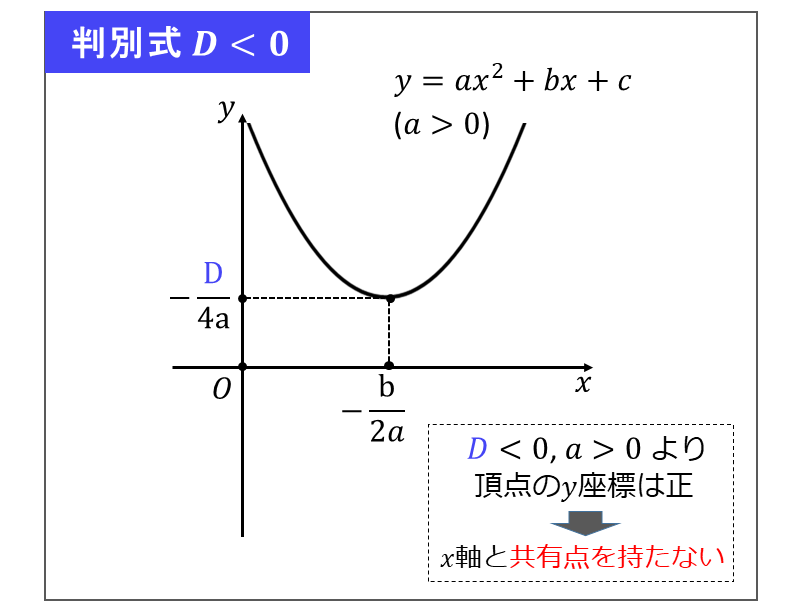
また、判別式が\(\large{D < 0 }\) のときは、二次関数の頂点の\(\large{y}\)座標は正となり、二次関数のグラフは\(\large{x}\)軸と共有点を持たないことが分かります。

(二次関数のグラフと判別式に関連する問題は後述しています。問題(3)～(4))

【3】二次方程式の判別式の問題

本章では、二次方程式の判別式に関連する問題について解説します。

問題(1) 二次方程式の判別式

与えられた二次方程式に判別式を使用します。 判別式は、 $$\large{D=b^2 -4ac}$$ であり、上式に\(\large{a=2,\hspace{2pt}b=5,\hspace{2pt}c=3}\)を代入します。 $$\large{D=5^2-4 \times 2 \times 3 = 1}$$

したがって、判別式が\(\large{D>0}\)であることから、二次方程式 \(\large{2x^2+5x+3 = 0}\) は2つの実数解を持ちます。

問題(2) 二次方程式の判別式

二次方程式の実数解が重解を持つ場合、 判別式は、 $$\large{D=b^2 -4ac=0}$$ の条件を満たします。ここで、\(\large{x}\) の係数が偶数であるため、\(\large{\frac{D}{4}}\) を計算します。

$$\large{\frac{D}{4}=b'^2 -ac=0}$$ 上式に \(\large{a=1,\hspace{2pt}b'=m,\hspace{2pt}c=2m-1}\) を代入します。 $$\large{\frac{D}{4}=m^2- (2m-1) =(m-1)^2}$$

\(\large{\frac{D}{4}=0}\) すなわち、以下の式を解きます。 $$\large{(m-1)^2 = 0}$$ したがって、与えられた二次方程式が重解を持つとき、\(\large{m=1}\) となります。

【4】二次関数のグラフと判別式の問題

本章では、二次関数のグラフと、判別式に関連する問題について解説します。

問題(3) 二次関数と判別式

二次関数が\(\large{x}\)軸と1点で接するとき、判別式\(\large{D}\) は以下の条件を満たします。 $$\large{D=b^2-4ac =0}$$ ここで、\(\large{x}\) の係数が偶数であるため、\(\large{\frac{D}{4}}\) を計算します。

$$\large{\frac{D}{4}=b'^2 -ac=0}$$ 上式に\(\large{a=1,\hspace{2pt}b'=m,\hspace{2pt}c=4m-3}\)を代入します。 $$\large{\frac{D}{4}=m^2- (4m-3) =(m-1)(m-3)}$$ したがって、\(\large{m}\)の条件は $$\large{\frac{D}{4}=(m-1)(m-3)=0}$$ よって、与えられた二次関数が\(\large{x}\)軸と1点で接するとき、\(\large{m=1,3}\) となります。

問題(4) 二次関数と判別式

与えられた二次関数の判別式\(\large{D}\)は以下のように求められます。 $$\large{D=b^2-4ac }$$ ここで、\(\large{x}\) の係数が偶数であるため、\(\large{\frac{D}{4}}\) を計算します。

$$\large{\frac{D}{4}=b'^2 -ac=0}$$ 上式に\(\large{a=1,\hspace{2pt}b'=1,\hspace{2pt}c=2m-3}\)を代入します。 $$\large{\frac{D}{4}=1^2- (2m-3) =-2m +4}$$

上記の判別式を、符号で場合分けすることにより、共有点の個数ごとの \(\large{m}\) の値を求めます。

共有点が2個であるとき、\(\large{\frac{D}{4}=-2m +4>0}\) から、\(\large{m}\) の値は \(\large{m < 2}\) となります。
共有点が1つ(重解)のときは、\(\large{\frac{D}{4}=-2m +4=0}\) から、\(\large{m}\)の値は \(\large{m=2}\) です。
また、共有点をもたないときは、\(\large{\frac{D}{4}=-2m +4 < 0}\) から、\(\large{m}\) の値は \(\large{m>2}\) となります。

---