二次方程式の因数分解による解法

本項では、因数分解を利用した二次方程式の問題と解き方について解説します。

【1】二次方程式の解法

二次方程式の解法の1つとして、因数分解を利用する方法があります。

例えば、以下のような二次方程式を解くとします。

問題の式の左辺を因数分解すると $$\large{x^2-4x+3 = (x-1)(x-3)}$$ と変形することができます。

ここで、2つの数 \(\large{A,\hspace{1pt}B}\) の積 $$\large{A \times B = 0}$$ であるとき、\(\large{A=0}\) または \(\large{B=0}\) が成り立ちます。

問題の二次方程式は $$\large{(x-1)(x-3) = 0}$$ であるため、\(\large{x-1=0}\) または \(\large{x-3=0}\) となります。したがって、 $$\large{x=1,\hspace{1pt}3}$$ と解くことができます。

因数分解の公式

二次方程式を解くときによく使用される 因数分解の公式を 以下にまとめます。

上記の公式を利用した計算問題は 【2】因数分解を利用する二次方程式の問題 で解説しています。

たすきがけの方法

上記の公式⑤の因数分解は たすきがけ といわれる方法で計算がしやすくなります。
たすきがけ は 以下の手順で行います。

　(1)『\(\large{x^2}\) の係数に一致する 2つの数の積 \(\large{\color{red}{a \times c}}\) を見つける』

　(2)『定数項 に一致する 2つの数の積 \(\large{\color{blue}{b \times d}}\) を見つける』

　(3)『\(\large{x}\) の係数が \(\large{\color{red}{a}\hspace{1pt}\color{blue}{d}\color{black}{}+\color{blue}{b}\hspace{1pt}\color{red}{c}}\) と一致する組み合わせを探す』

この (1)～(3) の手順を目で見てわかるように書いた図が以下のようになります。

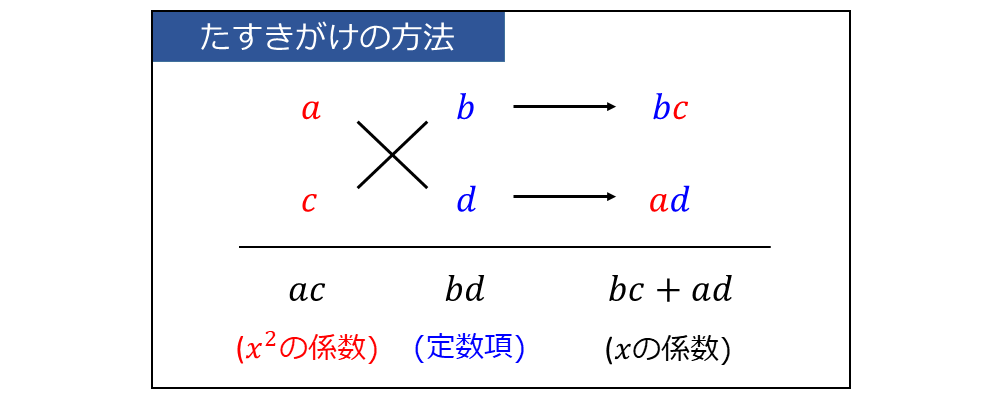
上図では、『×』の印が 斜めに位置している2つの項をかけることを意味します。

③の結果から、\(\large{(ax+b)(cx+d)}\) が因数分解された式となります。

たすきがけの計算例

例えば、以下のような二次方程式を解くとします。

　(1) \(\large{x^2}\) の係数 \(\large{3}\) に一致する 2つの数の積 は 『\(\large{\color{red}{3 \times 1}}\)』

　(2) 定数項 \(\large{-4}\) に一致する 2つの数の積 は 『\(\large{\color{blue}{-2 \times 2}}\)』 もしくは 『\(\large{\color{blue}{-1 \times 4}}\)』

　(3) たすきがけ の図から、\(\large{x}\) の係数である \(\large{4}\) は、定数項に一致する2つの数の積 が 『\(\large{\color{blue}{-2 \times 2}}\)』 であるときに得られることが分かります。

上図から、\(\large{(3x-2)(x+2)}\) が因数分解された式となります。

したがって、問題の二次方程式は $$\large{(3x-2)(x+2) = 0}$$ であることから、 $$\large{x=\frac{2}{3},\hspace{1pt}-2}$$ と解くことができます。

(上記の計算例の手順(1) では、『\(\large{\color{red}{3 \times 1}}\)』と『\(\large{\color{red}{-3 \times -1}}\)』の2つの組み合わせが考えられますが、得られる解は同じになります。そのため、『\(\large{\color{red}{3 \times 1}}\)』のみを候補にしています)

【2】因数分解を利用する二次方程式の問題

本章では、以下の因数分解を利用する二次方程式の問題と解き方について解説します。

問題(1)～(4)は、因数分解の公式①～④を利用して解く問題です。
(解答と解説 : 問題(1) 問題(2) 問題(3) 問題(4))

問題(5)～(7)は、因数分解の公式⑤ (たすきがけ) を利用して解く問題です。
(解答と解説 : 問題(5) 問題(6) 問題(7) 問題(8))

問題(1) 因数分解の公式の利用

【解答と解説】
因数分解の公式(1) $$\large{x^2 + 2ax + a^2 = (x+a)^2}$$ から、左辺を変形すると $$\large{x^2+12x+36=(x+6)^2}$$ したがって、問題の二次方程式は $$\large{(x+6)^2 = 0}$$ であるため、求める解は $$\large{x=-6}$$

問題(2) 因数分解の公式の利用

【解答と解説】
因数分解の公式(3) $$\large{x^2 - a^2 = (x+a)(x-a)}$$ から、左辺を変形すると $$\large{x^2-81=(x+9)(x-9)}$$ したがって、問題の二次方程式は $$\large{(x+9)(x-9) = 0}$$ であるため、求める解は $$\large{x=-9,\hspace{2pt}9}$$

問題(3) 因数分解の公式の利用

【解答と解説】
因数分解の公式(4) $$\large{x^2 +(a+b)x+ab = (x+a)(x+b)}$$ から、左辺を変形すると $$\large{x^2 +x -30 =(x+6)(x-5)}$$ したがって、問題の二次方程式は $$\large{(x+6)(x-5) = 0}$$ であるため、求める解は $$\large{x=-6,\hspace{2pt}5}$$

問題(4) 因数分解の公式の利用

【解答と解説】
因数分解の公式(2) $$\large{x^2 - 2ax + a^2 = (x-a)^2}$$ から、左辺を変形すると $$\large{x^2 -2\sqrt{5}x +5 =(x-\sqrt{5})^2}$$ したがって、問題の二次方程式は $$\large{(x-\sqrt{5})^2 = 0}$$ であるため、求める解は $$\large{x=\sqrt{5}}$$

問題(5) たすきがけによる因数分解

【解答と解説】
本問は、たすきがけによる因数分解 によって解きます。

問題の左辺に たすきがけ を利用すると、以下のような図で書き表されます。

したがって、問題の二次方程式を変形すると、 $$\large{(5x-4)(x+2) = 0}$$ であるため、求める解は $$\large{x=\frac{4}{5},\hspace{2pt}-2}$$

問題(6) たすきがけによる因数分解

【解答と解説】
本問は、たすきがけによる因数分解 によって解きます。

問題の左辺に たすきがけ を利用すると、以下のような図で書き表されます。

したがって、問題の二次方程式を変形すると、 $$\large{(2x+3)(x+2) = 0}$$ であるため、求める解は $$\large{x=-\frac{3}{2},\hspace{2pt}-2}$$

問題(7) たすきがけによる因数分解

【解答と解説】
本問は、たすきがけによる因数分解 によって解きます。

問題の左辺に たすきがけ を利用すると、以下のような図で書き表されます。

したがって、問題の二次方程式を変形すると、 $$\large{(2x-3)(2x+5) = 0}$$ であるため、求める解は $$\large{x=\frac{3}{2},\hspace{2pt}-\frac{5}{2}}$$

問題(8) たすきがけによる因数分解

【解答と解説】
本問は、たすきがけによる因数分解 によって解きます。

問題の式に \(\large{3}\) をかけると、 $$\large{3x^2 -5x-12 =0}$$ となります。

上式の左辺に たすきがけ を利用すると、以下のような図で書き表されます。

したがって、問題の二次方程式を変形すると、 $$\large{(3x+4)(x-3) = 0}$$ であるため、求める解は $$\large{x=-\frac{4}{3},\hspace{2pt}3}$$

---