定義域が動く二次関数の最大値・最小値
本項では、以下の定義域に 定数a を含む二次関数の問題について解説します。
\(\large{y=x^2-4x+5}\) の最大値・最小値を求めよ。
(ただし、\(\large{a>0}\) とする)
\(\large{y=x^2-4x+5}\) の最大値・最小値を求めよ。
問題(1)は 定義域の片側が 定数\(\large{a}\) である問題です。
また、問題(2)は 定義域の両端が 定数\(\large{a}\) の場合の問題です。
問題(1) 定義域の片側が動く二次関数
定義域の片側に 定数\(\large{a}\) を含む 二次関数の最大値・最小値 の問題について解説します。
\(\large{y=x^2-4x+5}\) の最大値・最小値を求めよ。
(ただし、\(\large{a>0}\) とする)
まず、問題の二次関数を平方完成して、軸と頂点を求めます。
$$\large{y=x^2-4x+5}$$ を平方完成すると、 $$\large{y=(x-2)^2+1}$$ となります。したがって、軸が \(\large{x=2}\)、頂点が \(\large{(2,1)}\) の二次関数であることが分かります。
二次関数の最大値・最小値は、軸の位置 と 定義域 の位置関係によって決まります。
本問では、定義域の片側が 定数\(\large{a}\) であるため、\(\large{a}\) の値によって最大値・最小値をとる \(\large{x}\) が変化してしまいます。
そこで、『グラフを描いて 定義域 と 軸 の関係を場合分けする』ことにより問題を解きます。
本問の二次関数の軸 (\(\large{x=2}\))、定義域 (\(\displaystyle \large{0\leqq x \leqq a}\)) に対してグラフを描いて整理すると、以下の①~④の4つに場合分けされます。
(下図では、定義域の範囲をピンク色で描いています。)


上記の 定数\(\large{a}\) と 軸の関係をまとめると、以下のようになります。
| \(\large{a}\) の条件 | 軸の位置 |
|---|---|
| ①\(\large{\hspace{2pt}0<\hspace{2pt}a< 2 }\) | 定義域外で右側 |
| ②\(\large{\hspace{2pt}2 \leqq a < 4}\) | 定義域内で右寄り |
| ③\(\large{\hspace{2pt}a =4}\) | 定義域の中間 |
| ④\(\large{\hspace{2pt}a > 4 }\) | 定義域内で左寄り |
上記のように、軸の位置を①~④に場合分けすることで 問題を解いていきます。
① 0 < a < 2 の場合 (軸が定義域外で右側)
軸\(\large{\hspace{1pt}(x=2\hspace{1pt})}\) の位置が定義域 \(\displaystyle \large{0\leqq x \leqq a}\) の外であり、右側の場合のグラフを下図に示します。

このとき、二次関数の軸が定義域の右側に位置するため、最小値は定義域の右側 (\(\large{x=a}\))、最大値は定義域の左側 (\(\large{x=0}\)) でとります。
したがって、
・\(\large{x=a}\) のとき最小値 \(\large{a^2-4a+5}\)
・\(\large{x=0}\) のとき最大値 \(\large{5}\)
となります。
② 2 ≦ a < 4 の場合 (軸が定義域内で右寄り)
軸\(\large{\hspace{1pt}(x=2\hspace{1pt})}\) が定義域 \(\displaystyle \large{0\leqq x \leqq a}\) に含まれ、軸が定義域の右寄りの場合のグラフを下図に示します。

このとき、二次関数の頂点が定義域に含まれることから、最小値は頂点 (\(\large{2,\hspace{1pt}1}\)) となります。
また、定義域のうち頂点から遠い側の端が最大値となるため、左側 (\(\large{x=0}\)) で最大値をとります。
したがって、
・\(\large{x=2}\) のとき最小値 \(\large{1}\)
・\(\large{x=0}\) のとき最大値 \(\large{5}\)
となります。
③ a=4 の場合 (軸が定義域の中間)
軸\(\large{\hspace{1pt}(x=2\hspace{1pt})}\) の位置が定義域 \(\displaystyle \large{0\leqq x \leqq a}\) の中間である場合のグラフを下図に示します。

このとき、頂点が定義域に含まれるため、最小値は頂点 \(\large{(2,\hspace{1pt}1)}\) となります。
また、頂点が定義域の中間に位置することから、最大値は、\(\large{x=0,\hspace{2pt}4}\) の2点でとります。
したがって、
・\(\large{x=2}\) のとき最小値 \(\large{1}\)
・\(\large{x=0,\hspace{2pt}4}\) のとき最大値 \(\large{5}\)
となります。
④ a > 4 の場合 (軸が定義域内で左寄り)
軸\(\large{\hspace{1pt}(x=a\hspace{1pt})}\) の位置が定義域 \(\displaystyle \large{0\leqq x \leqq a}\) の含まれ、軸が定義域の左寄りの場合のグラフを下図に示します。
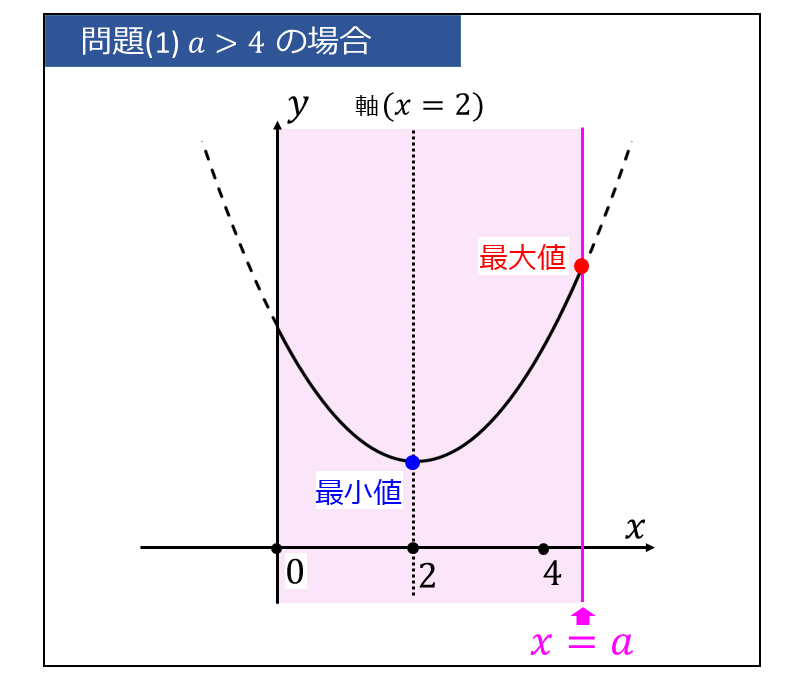
このとき、頂点が定義域に含まれることから、最小値は頂点 \(\large{(2,\hspace{1pt}1)}\) となります。
また、定義域のうち軸から遠い側の端が最大値となるため、右側 (\(\large{x=a}\)) で最大値をとります。
したがって、
・\(\large{x=2}\) のとき最小値 \(\large{1}\)
・\(\large{x=a}\) のとき最大値 \(\large{a^2-4a+5}\)
となります。
上記の①~④の結果をまとめると以下のようになります。
① \(\large{0 < a < 2\hspace{1pt}}\) のとき
\(\large{x=a}\) で最小値 \(\large{a^2-4a+5}\)
\(\large{x=0}\) で最大値 \(\large{5}\)
② \(\large{2 \leqq a < 4\hspace{1pt}}\) のとき
\(\large{x=2}\) で最小値 \(\large{1}\)
\(\large{x=0}\) で最大値 \(\large{5}\)
③ \(\large{a=4\hspace{1pt}}\) のとき
\(\large{x=2}\) で最小値 \(\large{1}\)
\(\large{x=0,\hspace{2pt}4}\) で最大値 \(\large{5}\)
④ \(\large{a > 4\hspace{1pt}}\) のとき
\(\large{x=2}\) で最小値 \(\large{1}\)
\(\large{x=a}\) で最大値 \(\large{a^2-4a+5}\)
問題(2) 定義域が動く二次関数 | 両端が動く場合
次に、以下の定数\(\large{a}\) を含む 二次関数の最大値・最小値 の問題について解説します。
\(\large{y=x^2-4x+5}\) の最大値・最小値を求めよ。
まず、前問と同様に二次関数を平方完成して、軸と頂点を求めます。
$$\large{y=x^2-4x+5}$$ を平方完成すると、 $$\large{y=(x-2)^2+1}$$ となります。したがって、軸が \(\large{x=2}\)、頂点が \(\large{(2,1)}\) の二次関数であることが分かります。
また、問題の二次関数は、定義域の両端に 定数\(\large{a}\) を含むため、問題(1)と同様に『グラフを描いて 軸 と 定義域 の関係を場合分け』して解きます。
本問の二次関数の軸 (\(\large{x=2}\))、定義域 (\(\displaystyle \large{a\leqq x \leqq a+2}\)) に対し グラフを描いて整理すると、以下の①~⑤の5つに場合分けされます。
(下図では、定義域の範囲をピンク色で描いています。)

上記の 定数\(\large{a}\) と 軸の関係を整理すると、以下の表のようになります。
| \(\large{a}\) の条件 | 軸の位置 |
|---|---|
| ①\(\large{\hspace{2pt}a < 0}\) | 定義域外で右側 |
| ②\(\large{\hspace{2pt}0 \leqq a < 1}\) | 定義域内で右寄り |
| ③\(\large{\hspace{2pt}a =1}\) | 定義域の中間 |
| ④\(\large{\hspace{2pt}1 < a \leqq 2}\) | 定義域内で左寄り |
| ⑤\(\large{\hspace{2pt}a > 2}\) | 定義域外で左側 |
上記の表のように、軸の位置を①~⑤に場合分けして問題を解いていきます。
① a < 0 の場合 (軸が定義域外で右側)
軸\(\large{\hspace{1pt}(x=a\hspace{1pt})}\) が定義域 \(\displaystyle \large{a\leqq x \leqq a+2}\) の外側であり、右側の場合のグラフを下図に示します。

このとき、二次関数の頂点が定義域の右側に位置するため、最小値は定義域の右側 (\(\large{x=a+2}\))、最大値は定義域の左側 (\(\large{x=a}\)) でとります。
したがって、
・\(\large{x=a+2}\) のとき最小値 \(\large{a^2+1}\)
・\(\large{x=a}\) のとき最大値 \(\large{a^2-4a+5}\)
となります。
② 0 ≦ a < 1 の場合 (軸が定義域内で右寄り)
軸\(\large{\hspace{1pt}(x=a\hspace{1pt})}\) の位置が定義域 \(\displaystyle \large{a\leqq x \leqq a+2}\) に含まれ、軸が定義域の右側 \(\large{(x=a+2)}\) に近い場合のグラフを下図に示します。

このとき、二次関数の頂点が定義域内に位置しており、最小値は頂点(\(\large{2,\hspace{1pt}1}\)) となります。
また、定義域のうち頂点から遠い側の端が最大値となるため、最大値は \(\large{x=a}\) でとります。
したがって、
・\(\large{x=2}\) のとき最小値 \(\large{1}\)
・\(\large{x=a}\) のとき最大値 \(\large{a^2-4a+5}\)
となります。
③ a = 1 の場合 (軸が定義域の中間)
軸\(\large{\hspace{1pt}(x=2\hspace{1pt})}\) の位置が定義域 \(\displaystyle \large{a\leqq x \leqq a+2}\) の中間である場合のグラフを下図に示します。
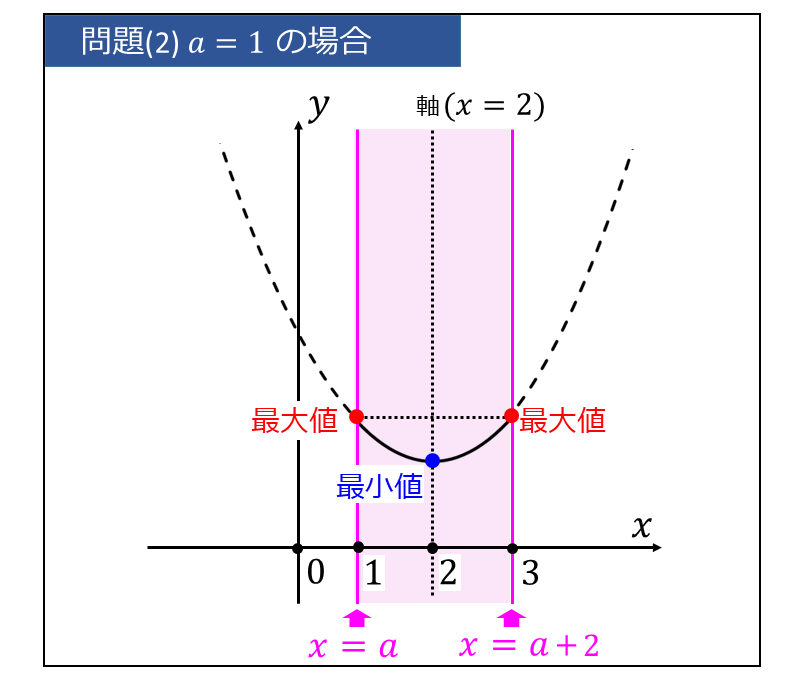
このとき、二次関数の頂点が定義域に含まれるため、最小値は頂点 \(\large{(2,\hspace{1pt}1)}\) となります。
また、頂点が定義域の中間にあるため、定義域の両端 (\(\large{x=a,\hspace{1pt}a+2}\)) で最大値をとります。
したがって、
・\(\large{x=2}\) のとき最小値 \(\large{1}\)
・\(\large{x=1,\hspace{2pt}3}\) のとき最大値 \(\large{2}\)
となります。
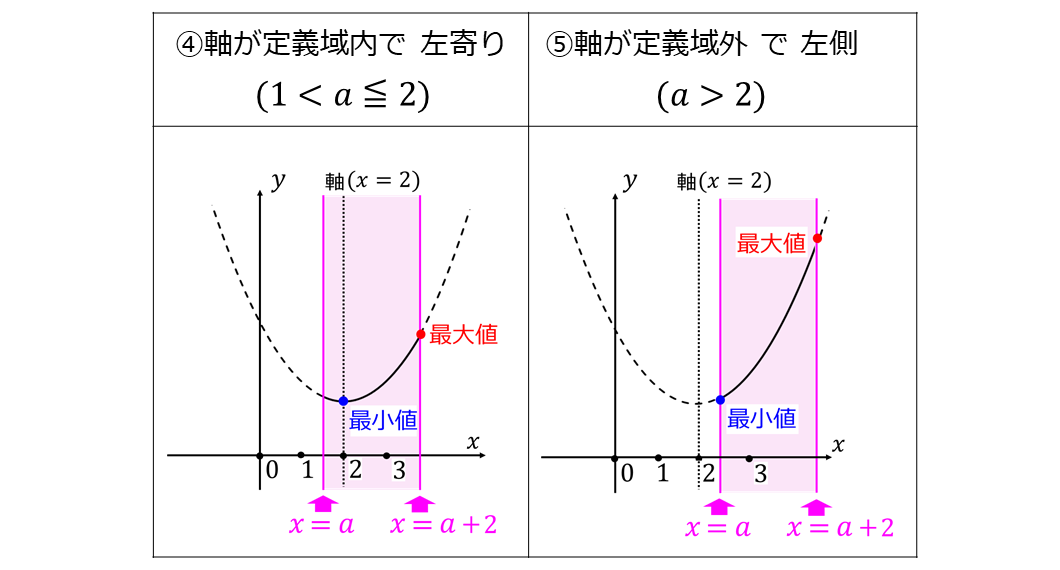
④ 1 < a ≦ 2 の場合 (軸が定義域内で左寄り)
軸\(\large{\hspace{1pt}(x=2\hspace{1pt})}\) の位置が定義域 \(\displaystyle \large{a\leqq x \leqq a+2}\) に含まれ、軸が定義域の左側に近い場合のグラフを下図に示します。

このとき、二次関数の頂点が定義域内に位置するため、最小値は頂点(\(\large{2,\hspace{1pt}1}\)) となります。
また、定義域のうち頂点から遠い側の端が最大値となるため、最大値は \(\large{x=a+2}\) でとります。
したがって、
・\(\large{x=2}\) のとき最小値 \(\large{1}\)
・\(\large{x=a+2}\) のとき最大値 \(\large{a^2+1}\)
となります。
⑤ a > 2 の場合 (軸が定義域外で左側)
軸\(\large{\hspace{1pt}(x=2\hspace{1pt})}\) の位置が定義域 \(\displaystyle \large{a\leqq x \leqq a+2}\) の外側であり、左側の場合のグラフを下図に示します。

このとき、二次関数の頂点が定義域の左側に位置するため、最小値は定義域の左側 (\(\large{x=a}\))、最大値は定義域の右側 (\(\large{x=a+2}\)) でとります。
したがって、
・\(\large{x=a}\) のとき最小値 \(\large{a^2-4a+5}\)
・\(\large{x=a+2}\) のとき最大値 \(\large{a^2+1}\)
となります。
上記の①~⑤の結果をまとめると以下のようになります。
① \(\large{a < 0\hspace{1pt}}\) のとき
・\(\large{x=a+2}\) で最小値 \(\large{a^2+1}\)
・\(\large{x=a}\) で最大値 \(\large{a^2-4a+5}\)
② \(\large{0 \leqq a < 1\hspace{1pt}}\) のとき
・\(\large{x=2}\) で最小値 \(\large{1}\)
・\(\large{x=a}\) で最大値 \(\large{a^2-4a+5}\)
③ \(\large{a=1\hspace{1pt}}\) のとき
・\(\large{x=2}\) で最小値 \(\large{1}\)
・\(\large{x=1,\hspace{2pt}3}\) で最大値 \(\large{2}\)
④ \(\large{1 < a \leqq 2\hspace{1pt}}\) のとき
・\(\large{x=2}\) で最小値 \(\large{1}\)
・\(\large{x=a+2}\) で最大値 \(\large{a^2+1}\)
⑤ \(\large{a > 2\hspace{1pt}}\) のとき
・\(\large{x=a}\) で最小値 \(\large{a^2-4a+5}\)
・\(\large{x=a+2}\) で最大値 \(\large{a^2+1}\)