二次不等式の解き方

本項では、二次不等式の解き方や問題について解説します。

【1】二次不等式の解き方

『\(\large{\hspace{1pt}x^2-4x+3 \geqq 0\hspace{1pt}}\)』 や 『\(\large{\hspace{1pt}2x^2 +7x + 6 < 0 \hspace{1pt}}\)』 など \(\large{x}\) の二次の項を含む不等式を 二次不等式 といいます。

二次不等式は、二次関数と\(\large{\hspace{1pt}x\hspace{1pt}}\)軸との位置関係に置き換えて解くことができます。

そのため、まず 二次方程式 \(\large{ax^2 + bx + c = 0}\) の解を求めた後、二次関数のグラフを描くことで解を求めることができます。

二次不等式を解く手順をまとめると、以下の①～③となります。

以下の例題から、上記の①～③による二次不等式の解き方を説明します。

・例題

◆【手順①】二次方程式 \(\large{ax^2 + bx + c = 0}\) を解く

まずは、二次方程式 \(\large{x^2 -4x + 3 = 0}\) を解きます。
二次方程式の解は、因数分解 や 解の公式 から求めます。

本問は、以下のように因数分解をすることができます。 $$\large{(x-1)(x-3)= 0}$$
すなわち、二次方程式の解は $$\large{x=1,\hspace{1pt}3}$$ となります。

◆【手順②】二次関数 \(\large{y=ax^2 + bx + c }\) を描く

二次不等式は \(\large{x}\) 軸との位置関係が分かればよいので、

　・二次方程式の解が \(\large{x=1,\hspace{1pt}3}\) である
　・\(\large{x^2}\) の係数が正であるため、下に凸のグラフ

の2点から、以下のようなグラフが描きます。

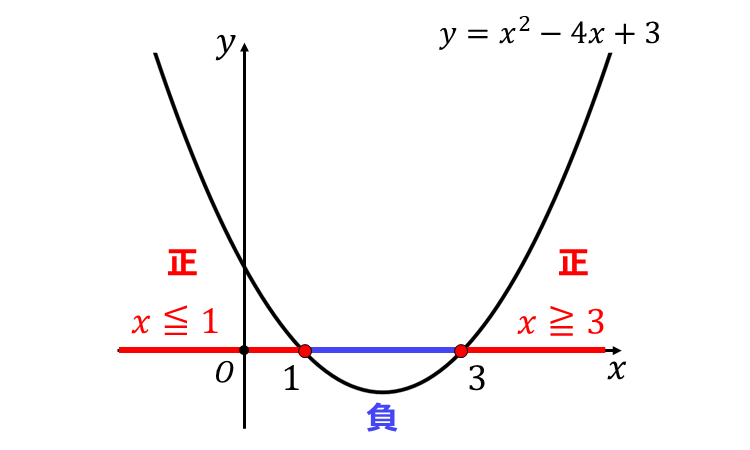
◆【手順③】グラフから 不等式を満たす \(\large{x}\) の範囲を読み取る

上記のグラフから、\(\large{x^2-4x+3 \geqq 0}\) を満たす範囲は、二次関数の \(\large{y}\) が正となる \(\large{x}\) の範囲を求めればよいので、 $$\large{x \leqq 1,\hspace{1pt}x \geqq 3 }$$ と読み取ることができます。

・二次不等式とグラフの対応

ここで、『二次関数のグラフ』と『二次不等式の解』の対応関係について整理します。

二次関数のグラフ は『\(\large{x}\)軸と\(\large{2}\)点で交わる』,『\(\large{x}\)軸と接する』,『\(\large{x}\)軸と共有点を持たない』という3つのパターンに分類して考えることができます。

それぞれのパターンは、判別式 $$\large{D=b^2 -4ac}$$ の符号と対応しており、

　・『\(\large{x}\)軸と\(\large{2}\)点で交わる』とき　　　\(\large{\hspace{5pt}D > 0}\)
　・『\(\large{x}\)軸と接する』とき　　　　　　\(\large{D = 0}\)
　・『\(\large{x}\)軸と共有点を持たない』とき　\(\large{D < 0}\)

となります。

以下の表に \(\large{ax^2+bx+c \geqq 0}\) (ただし、\(\large{a > 0\hspace{1pt}}\)) のグラフと解の関係をまとめます。

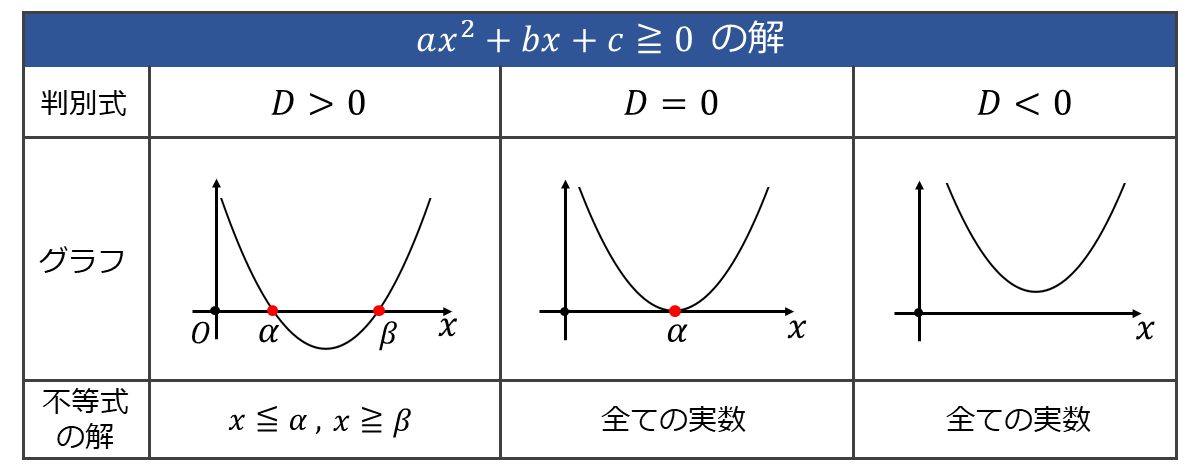
また、以下の表に \(\large{ax^2+bx+c > 0}\) (ただし、\(\large{a > 0\hspace{1pt}}\)) のグラフと解の関係をまとめます。

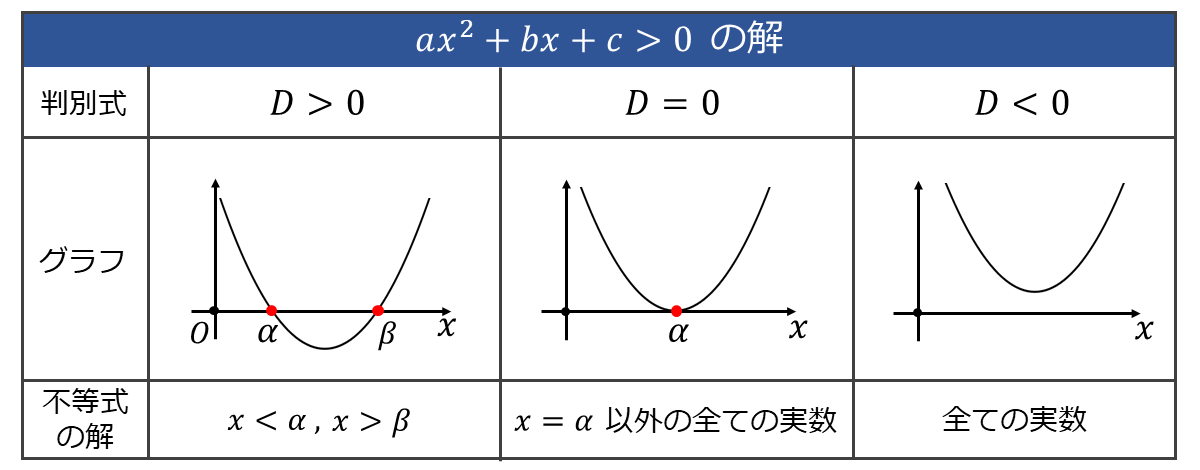
また、以下の表に \(\large{ax^2+bx+c \leqq 0}\) (ただし、\(\large{a > 0\hspace{1pt}}\)) のグラフと解の関係をまとめます。

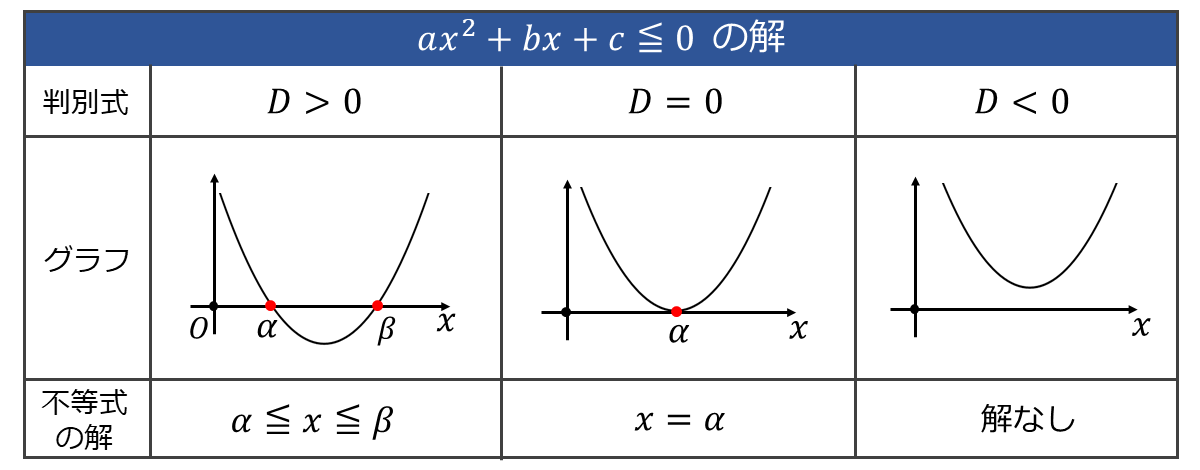
また、以下の表に \(\large{ax^2+bx+c \leqq 0}\) (ただし、\(\large{a > 0}\)) のグラフと解の関係をまとめます。

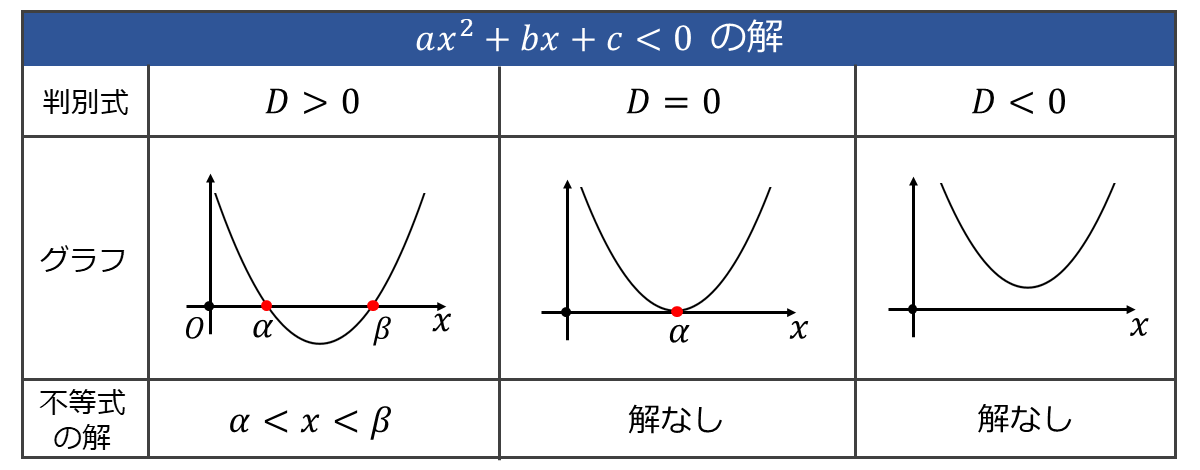
ここで、上の表ではすべて \(\large{a > 0}\) の条件でグラフと解の関係を示しましたが、\(\large{a < 0}\) の場合でも 二次不等式の両辺に \(\large{-1}\) をかけることで \(\large{a > 0}\) の場合と同様に解くことができます。

例えば、二次不等式 $$\large{-x^2+4x-3 < 0}$$ を解く場合は、両辺に \(\large{-1}\) をかけて $$\large{x^2-4x+3 > 0}$$ と \(\large{x^2}\) の係数を正として解くことができます。

【2】二次不等式の問題と解き方

本章では、二次不等式に関する問題と解き方について解説します。

問題(1)～(5)は、因数分解や解の公式を利用して 二次不等式の解を求める問題です。
(解答と解説 : 問題(1) 問題(2) 問題(3) 問題(4) 問題(5))

問題(6)は、定数を含む二次不等式が常に成り立つ条件を求める問題です。
(解答と解説 : 問題(6) )

問題1. 二次不等式_因数分解

【問題1の解答】
まず、二次方程式 $$\large{x^2 + x -20 = 0}$$ を解きます。因数分解の公式から、 $$\large{(x-4)(x+5)=0}$$ と変形されることから、二次方程式の解は、 $$\large{x=4,\hspace{1pt}-5}$$ と求められます。

ここで、二次関数 \(\large{y=x^2 + x -20}\) のグラフを描くと、以下のようになります。

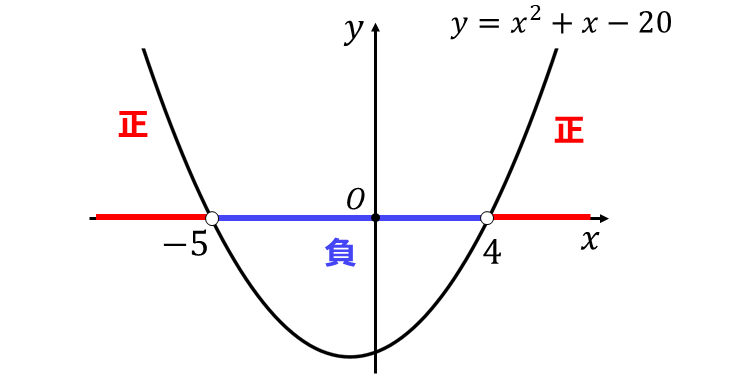
上記のグラフから、\(\large{y < 0}\) となる範囲を読み取ると、問題の二次不等式の解は、 $$\large{-5 < x < 4}$$ と求められます。

問題2.二次不等式_因数分解

【問題2の解答】
まず、二次方程式 $$\large{3x^2 + 4x -4 = 0}$$ を解きます。この二次方程式は、たすきがけによる因数分解から、 $$\large{(3x-2)(x+2)=0}$$ と変形されることから、二次方程式の解は、 $$\large{x=\frac{2}{3},\hspace{1pt}-2}$$ と求められます。

ここで、二次関数 \(\large{y=3x^2 + 4x -4}\) のグラフを描くと、以下のようになります。

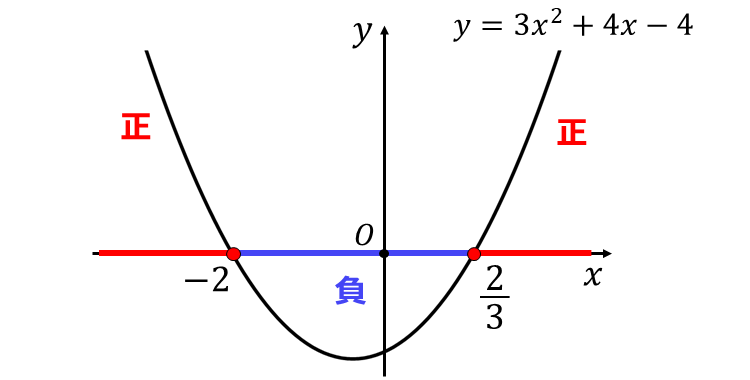
上記のグラフから、\(\large{y \geqq 0}\) となる範囲を読み取ると、問題の二次不等式の解は、 $$\large{x \leqq -2,\hspace{1pt}x \geqq \frac{2}{3}}$$ と求められます。

問題3.二次不等式_解の公式

【問題3の解答】
まず、問題の二次不等式は、\(\large{x^2}\) の係数が負であるため、両辺に \(\large{-1}\) をかけると、 $$\large{x^2 - 3x -2 < 0}$$ となります。二次方程式 $$\large{x^2 - 3x -2 = 0}$$ を解きます。この二次方程式は、解の公式 $$\large{x=\frac{-b \pm \sqrt{b^2 -4ac}}{2a}}$$ から、 \begin{eqnarray} \large x &\large=&\large \frac{-(-3) \pm \sqrt{(-3)^2 -4\times 1 \times(-2)}}{2\times 1}\\ \large &\large=&\large\frac{3 \pm \sqrt{17}}{2}\\ \end{eqnarray} と求められます。

ここで、二次関数 \(\large{y=x^2 - 3x -2}\) のグラフを描くと、以下のようになります。

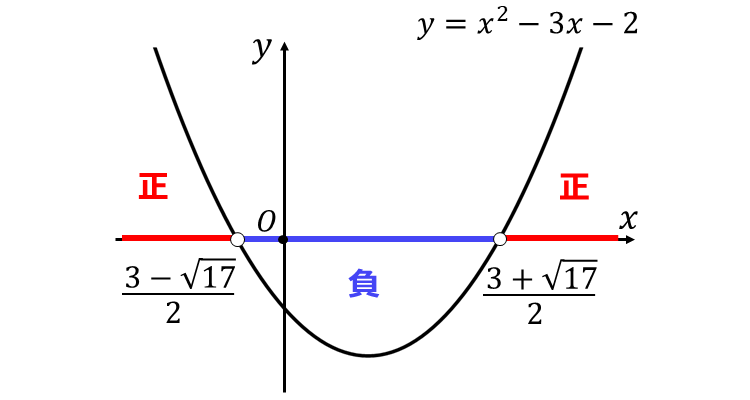
上記のグラフから、\(\large{y < 0}\) となる範囲を読み取ると、問題の二次不等式の解は、 $$\large{\frac{3 - \sqrt{17}}{2} < x < \frac{3 + \sqrt{17}}{2}}$$ と求められます。

問題4.二次不等式

【問題4の解答】
まず、二次方程式 $$\large{x^2 + 8x +16 = 0}$$ を解きます。因数分解の公式から、 $$\large{(x+4)^2=0}$$ と変形されることから、二次方程式の解は、 $$\large{x=-4}$$ と求められます。

ここで、二次関数 \(\large{y=x^2 + 8x +16}\) のグラフを描くと、以下のようになります。

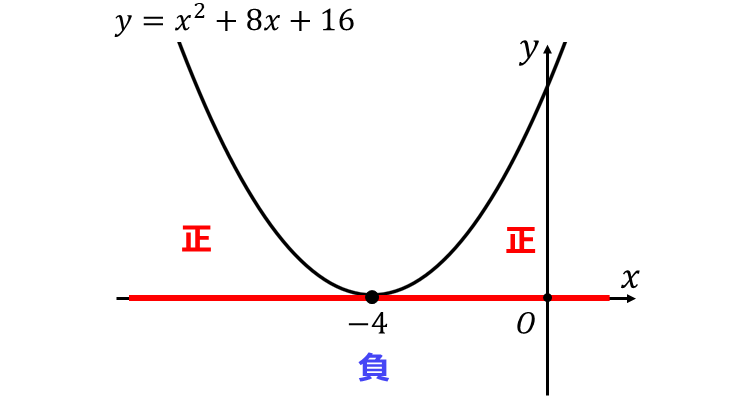
上記のグラフから、\(\large{y \leqq 0}\) となる範囲を読み取ると、問題の二次不等式の解は、 $$\large{x=-4}$$ と求められます。

問題5.二次不等式

【問題4の解答】
二次方程式 $$\large{x^2 + 4x +5 = 0}$$ の \(\large{x}\) の係数が偶数 (\(\large{b=2b\hspace{1pt}'}\)) の場合の判別式 $$\large{\frac{D}{4} = b\hspace{1pt}'^{\hspace{1pt}2} - a \hspace{1pt} c}$$ を計算すると、 $$\large{\frac{D}{4} = 2^2-1 \times 5 = -1}$$ から、二次関数のグラフ \(\large{y= x^2 + 4x +5}\) は \(\large{x}\)軸と共有点を持たないことが分かります。

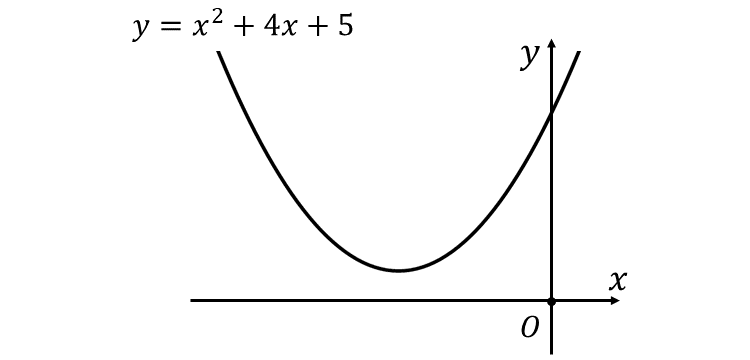
したがって、すべての実数 が解となります。

問題6.定数を含む二次不等式

【問題4の解答】
二次関数 $$\large{y=x^2 + mx -m+3}$$ と \(\large{x}\)軸の位置関係から、問題の二次不等式が成り立つ条件を求めます。

\(\large{x^2}\) の係数が正であることから、グラフは下に凸の形状となります。

二次不等式が常に正である場合、下に凸の二次関数のグラフが、\(\large{x}\)軸と共有点を持たない条件を求めればよいので、判別式 $$\large{D = b^2 -4\hspace{1pt}a\hspace{1pt}c < 0}$$ が条件となります。

判別式 \(\large{D}\) を計算すると、 \begin{eqnarray} \large D &\large=&\large m^2 -4(-m+3)\\[0.5em] \large &\large=&\large m^2 +4m -12\\[0.5em] \large &\large=&\large (m-2)(m+6)\\ \end{eqnarray}

すなわち、問題の二次不等式が成り立つとき、\(\large{D < 0 }\) となるので、\(\large{m}\) に関する二次不等式 $$\large{(m-2)(m+6)< 0 }$$ の解が、問題の二次不等式が成り立つ \(\large{m}\) の条件となります。

\(\large{m}\) に関する二次不等式を解くと、 $$\large{-6 < m < 2}$$ が求める \(\large{m}\) の条件となります。

---