二次関数の決定

二次関数の決定の問題とは、与えられた条件から二次関数の具体的な係数を求める問題です。

二次関数を決定する問題は、条件に対して適切な式を選択することが重要です。
本項では、問題のパターンに応じた解法について解説します。

1. 二次関数の決定の問題の解法
2. 二次関数の決定の問題
3. 応用問題 | 最大値・最小値、平行移動

【1】二次関数の決定の問題の解法

二次関数の決定の問題は、与えられた条件に対し適切な式を選択することが重要です。

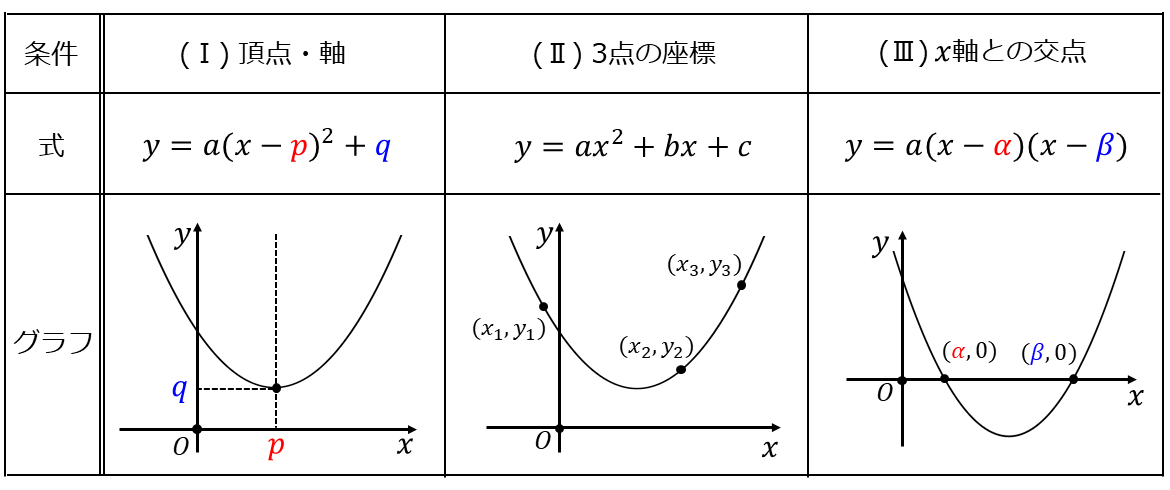
二次関数を決定するための条件として、主に以下の(Ⅰ)～(Ⅲ)の3つのパターンがあります。 $二次関数の決定の問題に使用する式$

(Ⅰ) 頂点や軸の位置が与えられた場合

二次関数を決定する条件として頂点や軸の位置が与えられた場合は、二次関数を平方完成した以下の式で考えます。 $$\large{y=a(x-p)^2 +q}$$ この式の場合、頂点の座標 $\large{(p,q)}$ を式にそのまま当てはめることができます。
残りの $\large{x^2}$ の係数 $\large{a}$ を別の条件から求めることで、二次関数を決定できます。

(Ⅱ) 3点の座標が与えられた場合

また、グラフが通過する3点の座標が与えられた場合は、二次関数の一般式で考えます。 $$\large{y=ax^2 + bx +c}$$ 3点の座標をそれぞれ上式に代入すると、係数 $\large{a,b,c}$ に関する3つの方程式が得られます。
得られた式を連立させ係数 $\large{a,b,c}$ を求めることで、二次関数を決定できます。

(Ⅲ) x軸との交点が与えられた場合

x軸との交点の座標を2点与えられた場合、二次関数を因数分解した形で表します。 $$\large{y=a(x-\alpha)(x-\beta)}$$ この式で表す場合、与えられた$\large{x}$軸との交点 ($\large{x=\alpha,\beta}$) を式の中にそのまま入れることができます。
残りの $\large{x^2}$ の係数 $\large{a}$ を別の条件から求めることで、二次関数を決定できます。

【2】二次関数の決定の問題

本章では、二次関数の決定の問題について解説します。

【2-1】軸・頂点が与えられた場合

【問題.1】

頂点が $\large{(3,6)}$ で、点 $\large{(1,-2)}$ を通る二次関数を求めよ。

二次関数の頂点が与えられているため、以下の式で表せます。 $$\large{y=a(x-3)^2+6}$$

点 $\large{(1,-2)}$ を通るとき、以下が成り立ちます。 $$\large{-2 = a(1-3)^2 +6}$$ $$\large{a=-2}$$ したがって、求める二次関数は以下の式となります。 $$\large{y=-2(x-3)^2+6}$$

【2-2】3点の座標が与えられた場合

【問題.2】

3点$\large{(-1,-8),\hspace{3pt}(2,-2),\hspace{3pt}(3,-4)}$を通る二次関数を求めよ。

与えられた条件が3点の座標であるため、以下の二次関数の式を使用します。 $$\large{y=ax^2+bx+c}$$

3点 $\large{(-1,-8),\hspace{3pt}(2,-2),\hspace{3pt}(3,-4)}$ をそれぞれ上式に代入すると、以下のようになります。 $$\large{-8=a-b+c}\hspace{10pt}\cdots(1)$$ $$\large{-2=4a+2b+c}\hspace{10pt}\cdots(2)$$ $$\large{-4=9a+3b+c}\hspace{10pt}\cdots(3)$$ $\large{(1)}$～$\large{(3)}$ を解いて係数 $\large{a,b,c}$ を求めます。

$\large{(1)-(2)}$から、 $$\large{-6=-3a-3b}\hspace{10pt}\cdots(4)$$ $\large{(2)-(3)}$から、 $$\large{2=-5a-b}\hspace{10pt}\cdots(5)$$

$\large{(4)-3\times (5)}$ より、 $$\large{-12=12a}$$ $$\large{a=-1}$$

$\large{(5)}$ に $\large{a=-1}$ を代入して $$\large{2=-5 \times (-1) -b}$$ $$\large{b=3}$$

$\large{(1)}$ に $\large{a=-1,b=3}$ を代入して $$\large{-8=-1 -3 +c}$$ $$\large{c=-4}$$

したがって、求める二次関数は以下の式となります。 $$\large{y=-x^2 + 3x -4}$$

【2-3】 x軸との交点が与えられた場合

【問題.3】

3点$\large{(2,0),\hspace{3pt}(-3,0),\hspace{3pt}(-1,18)}$を通る二次関数を求めよ。

与えられた3点のうち、$\large{(2,0),\hspace{3pt}(-3,0)}$ は $\large{x}$軸との交点です。
このような点が与えられた場合、$\large{y=a(x-\alpha)(x-\beta)}$ の式を使用することができます。

$\large{y=a(x-\alpha)(x-\beta)}$ の式を使用すると、未知の変数が $\large{a}$ の1つだけであるため、問題(2)と比較して簡単に二次関数を求めることができます。 $$\large{y=a(x-2)(x+3)}$$ 上式が点 $\large{(-1,18)}$ を通るとき、以下が成り立ちます。 $$\large{18 = a (-1-2)(-1+3)}$$ $$\large{a=-3}$$

したがって、求める二次関数は以下の式となります。 $$\large{y=-3(x-2)(x+3)}$$