二次不等式の計算ツール

本ツールは以下の計算結果を出力します。

• ・二次不等式の解
• ・対応する二次関数のグラフ

以下の黄色の枠内で 不等号の種類を選択し、二次不等式の係数 a, b, c (a≠0) を半角数字で入力した後、『計算実行』を押してください。

(1)二次不等式の解

(2)二次関数 y=ax²+bx+c のグラフ

(※当サイトの提供する計算結果や情報については一切責任は負いません。)

計算ツールの計算方法の説明

本計算ツールの計算方法について説明します。

計算方法

『\(\large{\hspace{1pt}x^2-4x+3 \geqq 0\hspace{1pt}}\)』 や 『\(\large{\hspace{1pt}x^2 +8x + 16 > 0 \hspace{1pt}}\)』などの二次不等式は、二次関数と \(\large{x\hspace{1pt}}\)軸との位置関係により解くことができます。

本計算ツールでは、判別式 $$\large{D=b^2-4ac}$$ を使用して、二次関数 \(\large{y=ax^2+bx+c}\) と \(\large{x\hspace{1pt}}\)軸との関係を求めます。

また、\(\large{x\hspace{1pt}}\)軸と交点が存在する場合は、解の公式 $$\large{\displaystyle \large{x = \frac{-b \pm \sqrt{b^2 -4ac}}{2a}}}$$ から \(\large{x\hspace{1pt}}\)軸との交点の値を求めます。

本計算ツールでは、『二次不等式の \(\large{x^2}\) の係数』,『判別式の符号』, 『解の公式』 の値から、二次関数と \(\large{x\hspace{1pt}}\)軸との位置関係を判定し 二次不等式の解を導きます。

計算の具体的な過程は、以下の計算例で説明します。

二次不等式の計算例

例えば、\(\large{\hspace{1pt}x^2-4x+3 \geqq 0\hspace{1pt}}\) を解く場合は、判別式 $$\large{D=(-4)^2-4\times 1 \times 3 = 4 >0}$$ より、二次関数 \(\large{y=x^2-4x+3}\) は \(\large{x\hspace{1pt}}\)軸と2つの交点を持つことがわかります。

また、二次方程式 $$\large{x^2-4x+3 = 0}$$ を解の公式から解くと、 $$\large{x=1,\hspace{1pt}3}$$ と求められます。

ここで、\(\large{x^2}\) の係数が正であることと、\(\large{x\hspace{1pt}}\)軸と2つの交点を持つことから、二次関数 \(\large{y= x^2-4x+3 }\) は以下のグラフとなります。

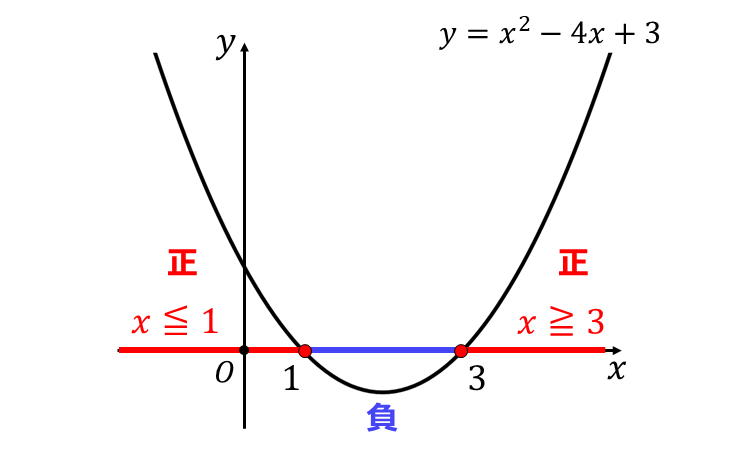
上記のグラフから、\(\large{x^2-4x+3 \geqq 0}\) を満たす範囲は、二次関数の \(\large{y}\) が正となる \(\large{x}\) の範囲となるので、 $$\large{x \leqq 1,\hspace{1pt}x \geqq 3 }$$ と求められます。

出力値の設定

『出力値の小数点以下の桁数』では、入力された桁より1つ小さい桁で出力値を四捨五入します。
 (例)『出力値の小数点以下の桁数』が2 → 出力が『10.59284...』の場合は、小数点以下3桁で四捨五入して『10.59』となります。

---