二次関数のグラフ

本項では、『二次関数のグラフの特徴』 や 『グラフと式の関係』、『グラフの書き方の問題』 などについて解説しています。

【1】二次関数のグラフの特徴

本章では、二次関数のグラフの特徴について解説します。

【1-1】y=ax²のグラフ

\(\large{y=ax^2}\) は二次関数の最も基本的な式です。
下図に\(\large{a}\)の符号が異なる \(\large{y=x^2}\) と \(\large{y=-x^2}\) のグラフを示します。

上図から、\(\large{y=ax^2}\) のグラフには以下のような特徴があります。

\(\large{a>0}\) の場合は最も小さい値(最小値)が存在し、その点を頂点といいます。
また、\(\large{a < 0}\) の場合は、最も大きい値(最大値)が頂点となります。

また、二次関数のグラフは頂点を通り、\(\large{y}\)軸に平行な直線に対して左右対称の形になります。この直線を、二次関数の軸といいます。

上図の \(\large{y=x^2}\) と \(\large{y=-x^2}\) のグラフでは、頂点の座標は(\(\large{0,0}\))、軸は \(\large{x=0}\) となります。

【1-2】y=a(x-p)²+qのグラフ | 頂点と軸

二次関数の一般式 \(\large{y=ax^2+bx +c}\) のグラフの頂点の座標は、式を平方完成することで求めることができます。

平方完成した二次関数は、以下の式で表されます。

このとき、上式の頂点の座標は\(\large{(p,q)}\)となります。

また、頂点の座標\(\large{(p,q)}\)と一般式の係数 \(\large{a,b,c}\) の関係は以下のようになります。 $$\large{p = -\frac{b}{2a} }$$ $$\large{q=-\frac{b^2 -4ac}{4a}}$$

\(\large{y=a(x-p)^2+q}\) のグラフは、\(\large{y= ax^2}\) のグラフを『\(\large{x}\)軸方向に\(\large{\hspace{1pt}+p\hspace{1pt}}\)、\(\large{y}\)軸方向に\(\large{\hspace{1pt}+q\hspace{1pt}}\)』だけ平行移動したグラフと一致します。

例えば、原点を頂点に持つ \(\large{y=x^2}\) を、『\(\large{x}\)軸方向に\(\large{\hspace{1pt}\color{red}{+3}\hspace{1pt}\color{black}{}}\)、\(\large{y}\)軸方向に\(\large{\hspace{1pt}\color{blue}{+2}\hspace{1pt}\color{black}{}}\)』だけ平行移動した二次関数は \(\large{y=(x-3)^2+2}\) です。このグラフの頂点は、下図に示すように\(\large{(3,2)}\)となります。

【1-3】y=a(x-α)(x-β)のグラフ | x軸との交点

二次関数 \(\large{y=ax^2+bx+c}\) から \(\large{y=a(x-\alpha)(x-\beta)}\)のような式に変形できる場合、二次関数は \(\large{x}\)軸に対して \(\large{(\alpha,0)}\) と \(\large{(\beta,0)}\) に交点を持ちます。

また、\(\large{\alpha = \beta}\) すなわち、\(\large{y=a(x-\alpha)^2}\) の式に変形できる場合は、二次関数は\(\large{x}\)軸と \(\large{(\alpha,0)}\) で接するグラフとなります。

交点の座標 \(\large{x=\alpha,\hspace{2pt}\beta}\) は、二次関数を因数分解するか、解の公式により求めることができます。

以下の図に、左から『\(\large{\boldsymbol{x}}\)軸と異なる2点で交わる場合』、『1点で接する場合』、『交点を持たない場合』の3つのパターンにおける、式の例とグラフを示します。

二次関数の\(\large{x}\)軸との交点の数は、判別式\(\large{D}\) を使用することで求めることができます。
判別式\(\large{D}\)は、二次関数 \(\large{y=ax^2+bx+c}\) において以下の式で計算されます。

二次関数が\(\large{x}\)軸と異なる2点で交わる場合、判別式は \(\large{D>0}\) となります。
また、\(\large{x}\)軸と1点で接する場合に判別式は \(\large{D=0}\)、共有点を持たない場合は \(\large{D < 0}\) となります。

(詳しくは、二次方程式の判別式で解説しています。)

【2】二次関数のグラフの問題

二次関数のグラフに関連した問題を解説します。

(1)二次関数のグラフの書き方

【グラフの書き方】
二次関数のグラフを書くときは、以下の4点から必要な情報を選んで考えます。

【解答と解説】
(1) まず、与えられた二次関数は \(\large{x^2}\) の係数が正の符号であるため、下に凸の形状をしています。

(2) また、二次関数を平方完成すると、 \begin{eqnarray} \large y &\large =&\large 2x^2 +4x +5\\ &\large =&\large 2(x^2 +2x)+5 \\ \large &\large =&\large 2(x^2 +2x +1^2 -1^2 ) +5 \\ \large &\large =&\large 2(x^2 +1)^2 +3 \\ \end{eqnarray} したがって、頂点の座標は \(\large{(-1,3)}\)、軸は \(\large{x=-1}\) となります。

(3) また、\(\large{y}\)切片は、\(\large{x=0}\) のときの \(\large{y}\) であるので、 $$\large{y= 5}$$ となります。

(4) また、頂点の座標が \(\large{(-1,3)}\) であることから、与えられた二次関数は \(\large{x}\)軸とは交わりません。

以上の情報から二次関数のグラフをかくと、以下のようになります。

(2)二次関数のグラフの書き方

【グラフの書き方】
前問と同じように、\(\large{x^2}\)の係数、頂点の座標などからグラフを書きます。
今回の問題では、簡単に因数分解ができるため、平方完成をせずに 頂点と軸を求めることができます。

【解答と解説】
(1) まず、与えられた二次関数は \(\large{x^2}\) の係数が負の符号であるため、上に凸の形状をしています。

(2),(4) 問題の二次関数は簡単に因数分解できるため、平方完成ではなく、因数分解から頂点の座標を求めます。 \begin{eqnarray} \large y &\large =&\large -x^2 +2x +8\\ &\large =&\large -(x^2 -2x -8) \\ \large &\large =&\large -(x+2)(x-4) \\ \end{eqnarray} したがって、与えられた二次関数は、\(\large{x}\)軸と \(\large{x=-2,\hspace{2pt}4}\) に交点を持ちます。

ここで、二次関数の軸に対して、\(\large{x}\)軸との2つの交点は対称であるため、交点のちょうど中間の位置に軸が存在します。

よって、二次関数の軸は \(\large{x=\frac{-2 + 4}{2} = 1}\) と求められます。

また、頂点の \(\large{y}\) 座標は、与えられた二次関数に \(\large{x=1}\) を代入して、 $$\large{y= 9}$$ と求められます。 したがって、頂点の座標は、 \(\large{(1,\hspace{2pt}9)}\) となります。

(3) また、\(\large{y}\)切片は、\(\large{x=0}\) のときの \(\large{y}\) であるので、 $$\large{y= 8}$$ となります。

以上の情報から二次関数のグラフをかくと、以下のようになります。

(3)二次関数のグラフの問題

【解答と解説】
(1)与えられた図から、二次関数は下に凸の形状のため、\(\large{a>0}\) となります。
(【1-1】y=ax^2のグラフの形状)

(2)また、二次関数の軸が\(\large{x}\)軸の正の位置にあるため、以下の式が成り立ちます。 $$\large{-\frac{b}{2a} >0}$$ \(\large{a>0}\) であるため、上記の不等式が成り立つためには、\(\large{b< 0 }\)
(【1-2】頂点と軸)

(3)\(\large{x=0}\) のとき、\(\large{y=c}\) となります。図から、\(\large{x=0}\) のとき \(\large{y>0}\) であることから、\(\large{c>0}\)となります。

(4)与えられた二次関数は、\(\large{x}\)軸に対して2つの異なる交点を持つことから、判別式 \(\large{D=b^2-4ac>0}\) となる。
(【1-3】x軸との交点)

(4)二次関数のグラフの問題

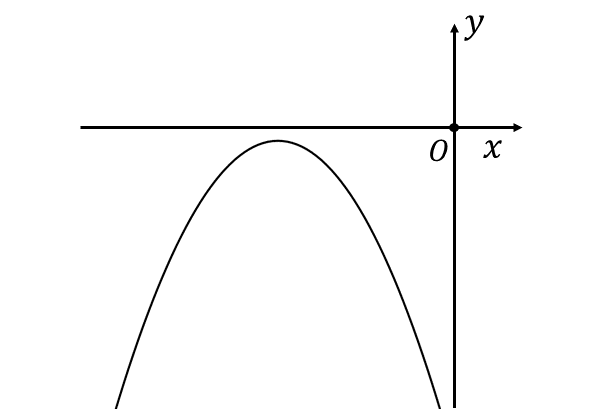
【解答と解説】
(1)与えられた図から、二次関数は上に凸の形状のため、\(\large{a < 0}\) となります。
(【1-1】y=ax^2のグラフの形状)

(2)また、軸の位置が\(\large{x}\)軸の負の領域であるため、以下の式が成り立ちます。 $$\large{-\frac{b}{2a} < 0}$$ \(\large{a < 0}\) であるため、上記の不等式が成り立つためには、\(\large{b < 0 }\) となります。
(【1-2】頂点と軸)

(3)\(\large{x=0}\) のとき、\(\large{y=c}\) となります。\(\large{x=0}\) のときの \(\large{y}\)軸との交点は図に示されていませんが、上に凸の二次関数の頂点の\(\large{y}\)座標が負 (すなわち、二次関数の最大値が負) であることから、\(\large{x=0}\) で \(\large{y < 0}\) となり、\(\large{c < 0}\) であることが分かります。

(4)図中の二次関数は、\(\large{x}\)軸に対して共有点を持たないことから、判別式 \(\large{D=b^2-4ac < 0}\) となります。
(【1-3】x軸との交点)

---