三角関数の性質
本項では以下の内容を解説しています。
- ・三角関数の性質の公式
- ・公式の証明
- ・関連する計算問題
【1】公式の一覧
本章では、三角関数の角度を変換する公式と意味の一覧をまとめます。
三角関数の性質を表す公式は、式を覚えるのではなく、角度\(\large{\theta}\) の変換の前後で 単位円上の\(\large{x}\)座標、\(\large{y}\)座標がどう変化するかを理解することが重要です。
三角関数の定義から、単位円上の\(\large{x}\)座標は\(\large{\cos \theta}\)、\(\large{y}\)座標は\(\large{\sin \theta}\) に対応するため、角度の変換により座標がどう変化するかを理解しておけば \(\large{\cos \theta}\)、\(\large{\sin \theta}\) の公式は簡単に導くことができます。
また、\(\large{\cos \theta}\)、\(\large{\sin \theta}\) の公式が分かれば、\(\large{\tan \theta}\) の公式は \(\displaystyle \large{\tan \theta = \frac{\sin \theta}{\cos \theta}}\) の式で求めることができます。
| 公式 | 意味 |
|---|---|
| \(\displaystyle \large{\sin (\theta+2n\pi)=\sin \theta}\) | 角度\(\large{\theta}\)が \(\large{2\pi}\) の整数(\(\large{n}\))倍だけ変化しても 動径は変化しない ⇒ 三角関数は不変 |
| \(\displaystyle \large{\cos (\theta+2n\pi)=\cos \theta}\) | |
| \(\displaystyle \large{\tan (\theta+2n\pi)=\tan \theta}\) |
(【2-1】\(\large{\theta+2n\pi }\)の公式)
| 公式 | 意味 |
|---|---|
| \(\displaystyle \large{\sin (-\theta)=-\sin \theta}\) | 角度 \(\large{-\theta}\) と \(\large{\theta}\) は単位円上で\(\large{x}\)軸対称 ・\(\large{x}\)座標は不変 ⇒ \(\large{\cos }\)の符号は不変 ・\(\large{y}\)座標は符号反転 ⇒ \(\large{\sin }\)の符号は反転 |
| \(\displaystyle \large{\cos (-\theta)=\cos \theta}\) | |
| \(\displaystyle \large{\tan (-\theta)=-\tan \theta}\) |
(【2-2】\(\large{-\theta }\)の公式の証明)
| 公式 | 意味 |
|---|---|
| \(\displaystyle \large{\sin (\theta + \pi)=-\sin \theta}\) | 角度 \(\large{\theta + \pi}\) と \(\large{\theta}\) は単位円上で原点対称 ・\(\large{x}\)座標は符号反転 ⇒ \(\large{\cos }\)の符号は反転 ・\(\large{y}\)座標は符号反転 ⇒ \(\large{\sin }\)の符号は反転 |
| \(\displaystyle \large{\cos (\theta + \pi)=-\cos \theta}\) | |
| \(\displaystyle \large{\tan (\theta + \pi)=\tan \theta}\) |
(【2-3】\(\large{\theta+\pi }\)の公式の証明)
| 公式 | 意味 |
|---|---|
| \(\displaystyle \large{\sin \left(\theta + \frac{\pi}{2}\right)=\cos \theta}\) | 角度 \(\large{\theta + \frac{1}{2}\pi}\) と \(\large{\theta}\) は単位円上で動径を \(\large{\frac{1}{2}\pi}\) 回転させた関係 ・\(\large{x}\)座標は\(\large{-y}\)と一致 ⇒ \(\large{\cos}\)は\(\large{-\sin}\)に変換 ・\(\large{y}\)座標は\(\large{x}\)と一致 ⇒ \(\large{\sin}\)は\(\large{\cos}\)に変換 |
| \(\displaystyle \large{\cos \left(\theta + \frac{\pi}{2}\right)=-\sin \theta}\) | |
| \(\displaystyle \large{\tan \left(\theta + \frac{\pi}{2}\right)=-\frac{1}{\tan \theta}}\) |
(【2-4】\(\large{\theta+\frac{\pi}{2} }\)の公式の証明)
【2】公式の証明
前章の三角関数の性質に関する公式の証明について解説します。
【2-1】θ+2nπの公式
角度\(\large{\theta}\)に対して、\(\large{2 \pi(=360°)}\) の整数倍だけ変化する場合、その動径の位置は変化しません。
したがって、整数を\(\large{n}\)としたときの 角度 \(\large{\theta + 2n\pi}\)の三角関数は、角度\(\large{\theta}\) の三角関数と一致します。
\(\displaystyle \large{\cos (\theta+2n\pi)=\cos \theta}\)
\(\displaystyle \large{\tan (\theta+2n\pi)=\tan \theta}\)
【2-2】-θの公式の証明
角度\(\large{-\theta}\) の三角関数は、以下の公式により変換されます。
\(\displaystyle \large{\cos (-\theta)=\cos \theta\hspace{8pt}}\)
\(\displaystyle \large{\tan (-\theta)=-\tan \theta}\)
上記の公式は、『三角関数の定義』と『単位円上の角度の位置関係』から、簡単に導くことができます。

三角関数の定義から、図の点\(\large{P(x,y)}\)の \(\large{y}\)座標が\(\large{\sin \theta}\)、\(\large{x}\)座標が\(\large{\cos \theta}\) の関係があります。 $$\large{x = \cos \theta}$$ $$\large{y = \sin \theta}$$
ここで、角度\(\large{-θ}\) の単位円上の位置を点\(\large{P'(x',y')}\)とすると、以下が成り立ちます。 $$\large{x' = \cos (-\theta)}$$ $$\large{y' = \sin (-\theta)}$$
下図のように、角度\(\large{\theta}\) と 角度\(\large{-\theta}\) の単位円上の位置は、\(\large{x}\)軸に関して対称な位置にあるため、 $$\large{x = x'}$$ $$\large{y = -y'}$$ となります。
したがって、以下の式が成り立ちます。 $$\large{\cos(-\theta) = \cos \theta}$$ $$\large{\sin(-\theta) = -\sin \theta}$$
\(\large{\tan \theta}\)に関しても同様に作図で求めるか、\(\displaystyle \large{\tan \theta = \frac{\sin \theta}{\cos \theta}}\) の式で確かめることができます。 $$\displaystyle \large{\tan (-\theta) = \frac{\sin (-\theta)}{\cos (-\theta)}=-\tan \theta}$$
【2-3】θ+πの公式の証明
角度\(\large{\theta + \pi}\) の三角関数は、以下の公式により変換されます。
\(\displaystyle \large{\cos (\theta + \pi)=-\cos \theta}\)
\(\displaystyle \large{\tan (\theta + \pi)=\tan \theta\hspace{5pt}}\)
三角関数の定義から、図の点\(\large{P(x,y)}\)の \(\large{y}\)座標が\(\large{\sin \theta}\)、\(\large{x}\)座標が\(\large{\cos \theta}\) の関係があります。
$$\large{x = \cos \theta}$$
$$\large{y = \sin \theta}$$
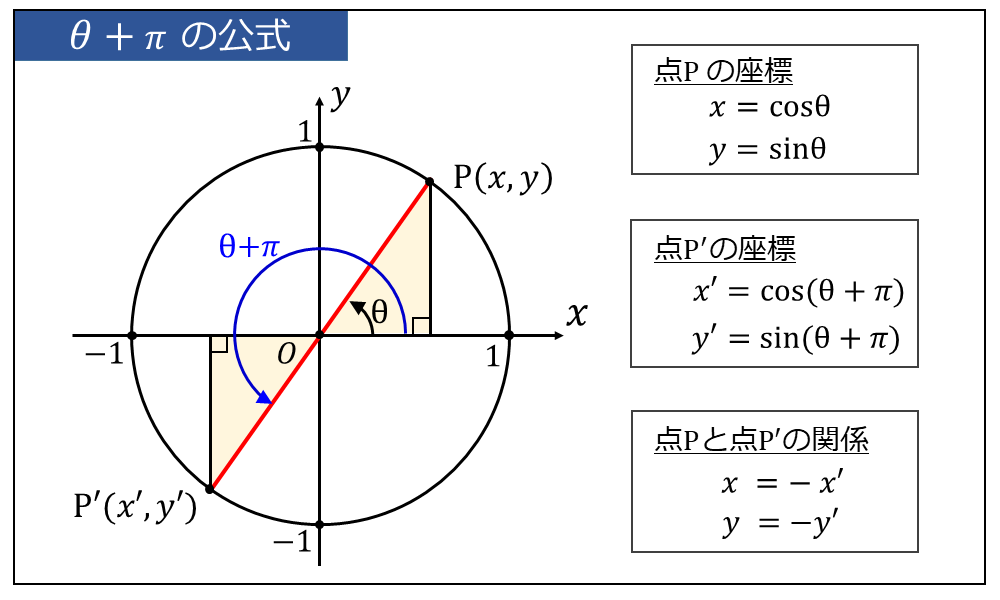
また、\(\large{\theta + \pi}\) の動径の位置を点\(\large{P'(x',y')}\) とすると、以下が成り立ちます。 $$\large{x' = \cos (\theta + \pi)}$$ $$\large{y' = \sin (\theta + \pi)}$$
ここで、点\(\large{P(x,y)}\) と 点\(\large{P'(x',y')}\)は原点対称の関係にあるため、 $$\large{x = -x'}$$ $$\large{y = -y'}$$ となります。
したがって、以下の式が成り立ちます。 $$\large{\cos(\theta + \pi) = -\cos \theta}$$ $$\large{\sin(\theta + \pi) = -\sin \theta}$$
三角関数の定義から \(\large{\tan \theta}\)は、動径の傾きを表します。上図で示されているように、赤線で描かれた動径は、角度が\(\large{\pi}\) 変化しても同じ傾きであるため、\(\large{\tan \theta}\) は変化しません。(もしくは、\(\displaystyle \large{\tan \theta = \frac{\sin \theta}{\cos \theta}}\) の式で確かめることができます。) $$\large{\tan(\theta + \pi) = \tan \theta}$$
【2-4】θ+π/2の証明
角度\(\large{\theta + \frac{1}{2}\pi}\) の三角関数は、以下の公式により変換されます。
三角関数の定義から、図の点\(\large{P(x,y)}\)の \(\large{y}\)座標が\(\large{\sin \theta}\)、\(\large{x}\)座標が\(\large{\cos \theta}\) の関係があります。
$$\large{x = \cos \theta}$$
$$\large{y = \sin \theta}$$

このとき、動径をさらに \(\large{\frac{1}{2}\pi}\) だけ回転させたときの動径の位置を 点\(\large{P'(x',y')}\) 以下が成り立ちます。 $$\large{x' = \cos (\theta + \frac{1}{2}\pi)}$$ $$\large{y' = \sin (\theta + \frac{1}{2}\pi)}$$
上図のように、動径を \(\large{\frac{1}{2}\pi}\) だけ回転させたとき、 $$\large{x = y'}$$ $$\large{y = -x'}$$ の関係があります。
したがって、以下の式が成り立ちます。 $$\large{\sin(\theta + \frac{1}{2}\pi) = \cos \theta}$$ $$\large{\cos(\theta + \frac{1}{2}\pi) = -\sin \theta}$$
また、\(\displaystyle \large{\tan \theta = \frac{\sin \theta}{\cos \theta}}\)から、 $$\large{\tan(\theta + \frac{1}{2}\pi) = -\frac{1}{\tan \theta}}$$
【補足】π-θ の公式の証明
また、上記の三角関数の性質から導かれる角度の変換公式として、角度\(\large{\pi - \theta}\) の公式があります。
\(\displaystyle \large{\cos (\pi -\theta)=-\cos \theta}\)
\(\displaystyle \large{\tan (\pi -\theta)=-\tan \theta}\)
上記の公式は、これまでの公式を変形することで導くことができます。
\(\large{\theta + \pi}\) の公式から、 $$\displaystyle \large{\sin (\theta + \pi)=-\sin \theta}$$ $$\displaystyle \large{\cos (\theta + \pi)=-\cos \theta}$$ $$\displaystyle \large{\tan (\theta + \pi)=\tan \theta\hspace{5pt}}$$ 上式の \(\large{\theta}\) を \(\large{-\theta}\) に変換すると、 $$\displaystyle \large{\sin (\pi-\theta)=-\sin (-\theta) = \sin \theta}$$ $$\displaystyle \large{\cos (\pi-\theta)=-\cos (-\theta) = -\cos \theta}$$ $$\displaystyle \large{\tan (\pi-\theta)=\tan (-\theta) =-\tan \theta}$$ と導くことができます。
【補足】π/2-θ の公式の証明
また、上記の三角関数の性質から導かれる角度の変換公式として、角度\(\large{\frac{1}{2}\pi - \theta}\) の公式があります。
上記の公式は、これまでの公式を変形することで導くことができます。
\(\large{\theta +\frac{1}{2} \pi}\) の公式から、 $$\displaystyle \large{\sin \left(\theta + \frac{1}{2} \pi\right)=\cos \theta}$$ $$\displaystyle \large{\cos \left(\theta + \frac{1}{2} \pi\right)=-\sin \theta}$$ $$\displaystyle \large{\tan \left(\theta + \frac{1}{2} \pi\right)=-\frac{1}{\tan \theta}}$$ 上式の \(\large{\theta}\) を \(\large{-\theta}\) に変換すると、 $$\displaystyle \large{\sin \left(\frac{1}{2} \pi-\theta\right)=\cos (-\theta) = \cos \theta}$$ $$\displaystyle \large{\cos \left(\frac{1}{2} \pi-\theta\right)=-\sin (-\theta) = \sin \theta}$$ $$\displaystyle \large{\tan \left(\frac{1}{2} \pi-\theta\right)=-\frac{1}{\tan (-\theta)} =\frac{1}{\tan \theta}}$$ と導くことができます。
【3】三角関数の性質の問題
本章では、以下の(1)~(5)の三角関数の性質の問題について解説します。
(1)2nπより角度が大きい場合 | sinの計算
\(\displaystyle \large{\sin \left(\frac{13}{4}\pi\right)}\)
【解答と解説】
まず、三角関数の \(\large{\theta + 2n\pi}\) の公式から、角度を \(\large{2\pi}\) より小さくします。
$$\displaystyle \large{\sin (\theta+2n\pi)=\sin \theta}$$
$$\displaystyle \large{\cos (\theta+2n\pi)=\cos \theta}$$
$$\displaystyle \large{\tan (\theta+2n\pi)=\tan \theta}$$
を与えられた式に適応すると、
$$\displaystyle \large{\sin \frac{13}{4}\pi = \sin \left(\frac{5}{4}\pi + 2\pi\right)=\sin \frac{5}{4}\pi}$$
となります。
次に、三角関数の \(\large{\theta + \pi}\) の公式から、角度を \(\large{\pi}\) より小さくします。 $$\displaystyle \large{\sin (\theta + \pi)=-\sin \theta}$$ $$\displaystyle \large{\cos (\theta + \pi)=-\cos \theta}$$ $$\displaystyle \large{\tan (\theta + \pi)=\tan \theta\hspace{5pt}}$$ を与えられた式に適応すると、 $$\displaystyle \large{\sin \frac{5}{4}\pi = \sin \left(\frac{1}{4}\pi + \pi\right)=-\sin \frac{1}{4}\pi}$$ となります。
したがって、 $$\large{\sin \left(\frac{13}{4}\pi\right) = -\sin \frac{1}{4}\pi = -\frac{1}{\sqrt{2}}}$$
(2)角度が負の場合 | cosの計算
\(\displaystyle \large{\cos \left(-\frac{5}{6}\pi\right)}\)
【解答と解説】
まず、三角関数の \(\large{-\theta}\) の公式から、角度を正の値に変換します。
$$\displaystyle \large{\sin (-\theta)=-\sin \theta}$$
$$\displaystyle \large{\cos (-\theta)=\cos \theta\hspace{8pt}}$$
$$\displaystyle \large{\tan (-\theta)=-\tan \theta}$$
を与えられた式に適応すると、
$$\displaystyle \large{\cos -\frac{5}{6}\pi = \cos \frac{5}{6}\pi}$$
となります。
次に、三角関数の \(\large{\theta + \frac{1}{2} \pi}\) の公式から、角度を \(\large{\frac{1}{2} \pi}\) より小さくします。 $$\displaystyle \large{\sin \left(\theta + \frac{1}{2} \pi\right)=\cos \theta}$$ $$\displaystyle \large{\cos \left(\theta + \frac{1}{2} \pi\right)=-\sin \theta}$$ $$\displaystyle \large{\tan \left(\theta + \frac{1}{2} \pi\right)=-\frac{1}{\tan \theta}}$$ を与えられた式に適応すると、 $$\displaystyle \large{\cos \frac{5}{6}\pi = \cos \left(\frac{2}{6}\pi + \frac{1}{2}\pi\right)=-\sin \frac{1}{3}\pi}$$ となります。
したがって、 $$\large{\cos \left(-\frac{5}{6}\pi\right) = -\sin \frac{1}{3}\pi = -\frac{\sqrt{3}}{2}}$$ と求められます。
(3)π/2より大きい角度の場合 | tanの計算
\(\displaystyle \large{\tan \left(\frac{2}{3}\pi\right)}\)
【解答と解説】
三角関数の \(\large{\theta + \frac{1}{2} \pi}\) の公式から、角度を \(\large{\frac{1}{2} \pi}\) より小さくします。 $$\displaystyle \large{\sin \left(\theta + \frac{1}{2} \pi\right)=\cos \theta}$$ $$\displaystyle \large{\cos \left(\theta + \frac{1}{2} \pi\right)=-\sin \theta}$$ $$\displaystyle \large{\tan \left(\theta + \frac{1}{2} \pi\right)=-\frac{1}{\tan \theta}}$$ を与えられた式に適応すると、 $$\displaystyle \large{\tan \frac{2}{3}\pi = \tan \left(\frac{1}{6}\pi + \frac{1}{2}\pi\right)=-\frac{1}{\tan \frac{1}{6}\pi}}$$ となります。
したがって、 $$\large{\tan \left(\frac{2}{3}\pi\right) = -\frac{1}{\tan \frac{1}{6}\pi} = -\sqrt{3}}$$ と求められます。
(4)直接に値を求められない三角関数 | sinとcosの計算
\(\displaystyle \large{\cos \left(\frac{5}{8}\pi\right) - \sin\left(\frac{9}{8}\pi\right) }\)
【解答と解説】
\(\displaystyle \large{\cos \left(\frac{5}{8}\pi\right)}\)や、\(\displaystyle \large{\sin\left(\frac{9}{8}\pi\right)}\) は直接に三角関数の値を求めることができません。
そこで、三角関数の性質を利用して、角度を変換して式を変形してみます。
まず、三角関数の \(\large{\theta + \frac{1}{2} \pi}\) の公式から、 $$\displaystyle \large{\sin \left(\theta + \frac{1}{2} \pi\right)=\cos \theta}$$ $$\displaystyle \large{\cos \left(\theta + \frac{1}{2} \pi\right)=-\sin \theta}$$ $$\displaystyle \large{\tan \left(\theta + \frac{1}{2} \pi\right)=-\frac{1}{\tan \theta}}$$ を与えられた式の第一項に適応すると、 $$\displaystyle \large{\cos \left(\frac{5}{8}\pi\right) = \cos \left(\frac{1}{8}\pi + \frac{1}{2}\pi\right)=-\sin\left(\frac{1}{8}\pi\right)}$$ となります。
次に、三角関数の \(\large{\theta + \pi}\) の公式から、 $$\displaystyle \large{\sin (\theta + \pi)=-\sin \theta}$$ $$\displaystyle \large{\cos (\theta + \pi)=-\cos \theta}$$ $$\displaystyle \large{\tan (\theta + \pi)=\tan \theta\hspace{5pt}}$$ を与えられた式の第二項に適応すると、 $$\displaystyle \large{\sin \frac{9}{8}\pi = \sin \left(\frac{1}{8}\pi + \pi\right)=-\sin\left(\frac{1}{8}\pi\right)}$$ となります。
したがって、 $$\large{\cos \left(\frac{5}{8}\pi\right) - \sin\left(\frac{9}{8}\pi\right)=0}$$ と求められます。
(5)直接に値を求められない三角関数の値 | tanの計算
\(\displaystyle \large{\tan \left(-\frac{1}{10}\pi\right) \times \tan\left(\frac{3}{5}\pi\right) }\)
【解答と解説】
前問と同様に、\(\displaystyle \large{\tan \left(-\frac{1}{10}\pi\right)}\)や、\(\displaystyle \large{\tan\left(\frac{3}{5}\pi\right)}\) は直接に三角関数の値を求めることができないため、三角関数の性質を利用して式を変形します。
まず、三角関数の \(\large{-\theta}\) の公式から、 $$\displaystyle \large{\sin (-\theta)=-\sin \theta}$$ $$\displaystyle \large{\cos (-\theta)=\cos \theta\hspace{8pt}}$$ $$\displaystyle \large{\tan (-\theta)=-\tan \theta}$$ を与えられた式の第一項に適応すると、 $$\displaystyle \large{\tan \left(-\frac{1}{10}\pi\right) = -\tan \left(\frac{1}{10}\pi\right)}$$ となります。
次に、三角関数の \(\large{\theta + \frac{1}{2} \pi}\) の公式から、 $$\displaystyle \large{\sin \left(\theta + \frac{1}{2} \pi\right)=\cos \theta}$$ $$\displaystyle \large{\cos \left(\theta + \frac{1}{2} \pi\right)=-\sin \theta}$$ $$\displaystyle \large{\tan \left(\theta + \frac{1}{2} \pi\right)=-\frac{1}{\tan \theta}}$$ を与えられた式の第二項に適応すると、 \begin{eqnarray} \large \tan \left(\frac{3}{5}\pi\right)&\large =&\large \tan \left(\frac{1}{10}\pi + \frac{1}{2}\pi\right) \\ \large &\large =&\large -\frac{1}{\tan \left(\frac{1}{10}\pi\right)} \\ \end{eqnarray} となります。
したがって、 $$\large{\tan \left(-\frac{1}{10}\pi\right) \times \tan\left(\frac{3}{5}\pi\right) = 1}$$ と求められます。