三角比の余弦定理
【1】余弦定理の公式と使い方
余弦定理とは、三角形\(\large{\mathrm{ A\hspace{1pt}B\hspace{1pt}C }}\) の辺の長さ (\(\large{\hspace{1pt}a,b,c\hspace{2pt}}\)) と 角度 (\(\large{\mathrm{ A,\hspace{1pt}B,\hspace{1pt}C }}\)) に対して成り立つ等式のことをいいます。
辺\(\large{\mathrm{\overline{BC}}}\) の長さ\(\large{a}\) を求める余弦定理は、辺\(\large{\mathrm{\overline{AC},\hspace{2pt}\overline{AB}}}\) の長さ \(\large{b,\hspace{2pt}c}\) と 辺\(\large{\mathrm{\overline{BC}}}\) に向かい合う角度\(\large{\mathrm{A}}\) の 余弦\(\large{\mathrm{(\cos A)}}\) を用いて以下の式で表されます。

上式は 3つの辺 (\(\large{\hspace{1pt}a,b,c\hspace{2pt}}\)) についてそれぞれ成り立ちます。3つの辺 (\(\large{\hspace{1pt}a,b,c\hspace{2pt}}\)) の余弦定理をまとめると、以下のようになります。
・辺の長さの求め方
余弦定理は、三角形の形状 (辺の長さや角度) を求めるためによく使用されます。
三角形\(\large{\mathrm{ A\hspace{1pt}B\hspace{1pt}C }}\) の2辺の長さ \(\large{b,\hspace{1pt}c}\) と、その2辺の間に位置する角\(\large{\mathrm{ A}}\) の 余弦(\(\large{\cos \mathrm{ A}}\)) の値が分かれば、辺\(\large{\mathrm{ \overline{BC}}}\) の長さ \(\large{a}\) を求めることができます。
辺の長さ\(\large{a}\) は正の値であるため、辺の長さ\(\large{a}\) を求める余弦定理は $$\large{a= \sqrt{b^2 + c^2 -2 \hspace{1pt}b\hspace{1pt}c \cos \mathrm{ A}}}$$ と表されます。
同様に、辺の長さ\(\large{b,\hspace{1pt}c}\) を求める余弦定理は $$\large{b^2 = \sqrt{c^2 + a^2 -2\hspace{1pt} c\hspace{1pt}a \cos \mathrm{ B}}}$$ $$\large{c^2 = \sqrt{a^2 + b^2 -2\hspace{1pt} a\hspace{1pt}b \cos \mathrm{ C}}}$$ と表されます。
・角度の求め方
一方、3つの辺の長さ \(\large{(\hspace{1pt}a,b,c\hspace{2pt})}\) が判明していれば、角\(\large{\mathrm{ A}}\) の 余弦(\(\large{\cos\mathrm{ A}}\)) の値を以下のように求められます。
角\(\large{\mathrm{ B}}\)、角\(\large{\mathrm{ C}}\) についても同様に式が成り立つため、3つの辺の長さ \(\large{(\hspace{1pt}a,b,c\hspace{2pt})}\) が判明していれば、3つの頂点の角度 (\(\large{\mathrm{ A,\hspace{1pt}B,\hspace{1pt}C\hspace{2pt}}}\)) の余弦を求めることができます。 $$\large{\cos \mathrm{ B} = \frac{a^2 + c^2 - b^2}{2 a\hspace{1pt}c}}$$ $$\large{\cos \mathrm{ C} = \frac{a^2 + b^2 - c^2}{2 a\hspace{1pt}b}}$$
余弦定理から 辺の長さや角度の大きさを求める計算問題は 後述の余弦定理の問題 で解説しています。
また、本サイトでは、余弦定理から辺の長さ, 角度の大きさを求める計算ツールを公開しています。(余弦定理の計算ツール)
・鋭角と鈍角の判定
また、\(\large{\cos \mathrm{ A}}\) は
・鋭角(\(\large{\hspace{1pt}0^\circ < \mathrm{ A} < 90^\circ\hspace{1pt}}\)) のとき \(\large{\hspace{5pt}\cos \mathrm{ A} >0}\)
・直角(\(\large{\hspace{1pt}\mathrm{ A} = 90^\circ\hspace{1pt}}\)) のとき \(\large{\hspace{8pt}\cos \mathrm{ A} =0}\)
・鈍角(\(\large{\hspace{1pt}90^\circ < \mathrm{ A} < 180^\circ\hspace{1pt}}\)) のとき \(\large{\hspace{2pt}\cos \mathrm{ A} < 0}\)
の値をとります。
したがって、余弦定理から求められる \(\large{\cos \mathrm{ A}}\) の符号から、『三角形の角度\(\large{\mathrm{ A}}\) の鋭角, 直角, 鈍角の判定をすることができます。』
角度\(\large{\mathrm{ A}}\) の鋭角, 直角, 鈍角のときに対応する \(\large{\cos \mathrm{ A}}\) の符号 と 辺の長さの関係 を以下の表に示します。
| 角度A | 鋭角 | 直角 | 鈍角 |
|---|---|---|---|
| \(\large{\cos \mathrm{ A}}\) の符号 |
\(\large{+}\) | \(\large{0}\) | \(\large{-}\) |
| 辺の 条件 |
\(\large{b^2 + c^2 > a^2}\) | \(\large{b^2 + c^2 = a^2}\) | \(\large{b^2 + c^2 < a^2}\) |
上記の表の『辺の条件』は、余弦定理から得られます。 $$\large{\cos \mathrm{ A} = \frac{b^2 + c^2 - a^2}{2\hspace{1pt} b\hspace{1pt}c}}$$ 上記の余弦定理の分母 \(\large{2\hspace{1pt}b\hspace{1pt}c}\) は正であるため、\(\large{\cos \mathrm{ A}}\) の符号は 分子 \(\large{b^2 + c^2 - a^2}\) の符号によって決まります。
例えば、\(\large{b^2 + c^2 > a^2}\) であるとき、\(\large{\cos \mathrm{ A}}\) が正となることから 角\(\large{\mathrm{ A}}\) は鋭角となります。
(鋭角、直角、鈍角を判定する計算問題は問題(3)で解説しています。)
【2】余弦定理の証明
本章では、余弦定理の証明について解説します。
三角形\(\large{\mathrm{ A\hspace{1pt}B\hspace{1pt}C }}\) を、頂点\(\large{\mathrm{A}}\) が原点、辺\(\large{\overline{\mathrm{AB}}}\) が \(\large{x}\) 軸上になるように、\(\large{xy}\) 座標上に配置します。
頂点\(\large{\mathrm{C}}\) から辺\(\large{\overline{\mathrm{AB}}}\) に垂線を下し、その垂線の足を点\(\large{\mathrm{H}}\) とします。
このとき、角\(\large{\mathrm{A}}\) が鋭角、垂直、鈍角の3つの場合について証明し、余弦定理を導きます。
・角Aが鋭角である場合
角\(\large{\mathrm{A}}\)が鋭角であり、点\(\large{\mathrm{C}}\) からの垂線の足\(\large{\mathrm{H}}\) が辺\(\large{\overline{\mathrm{AB}}}\) の内側である場合は、以下の図のようになります。

図に示すように、点\(\large{\mathrm{C}}\) の座標は、\(\large{(x,y)=(b \cos \mathrm{A}, b \sin \mathrm{A})}\) となります。
このとき、点\(\large{\mathrm{C}}\) からの垂線の足\(\large{\mathrm{H}}\)と、点\(\large{\mathrm{B}}\) までの距離は、点\(\large{\mathrm{B}}\) の\(\large{x}\)座標から 点\(\large{\mathrm{H}}\) の\(\large{x}\)座標の差分をとり、以下のようになります。 $$\large{\overline{\mathrm{HB}} = c-b \cos \mathrm{A}}$$
ここで、三角形\(\large{\mathrm{ C\hspace{1pt}H\hspace{1pt}B }}\) (図中の黄色部分) に着目し、三平方の定理を使用すると、以下のようになります。 \begin{eqnarray} \large a^2&\large=&\large (b \sin \mathrm{A})^2 + (c-b \cos \mathrm{A})^2 \\[0.5em] &\large=&\large b^2 \sin^2 \mathrm{A} + c^2 -2 \hspace{1pt}b\hspace{1pt}c \cos \mathrm{A} + b^2 \cos^2 \mathrm{A}\\[0.5em] \large &\large=&\large b^2 (\sin^2 \mathrm{A} + \cos^2 \mathrm{A}) + c^2 -2\hspace{1pt} b\hspace{1pt}c \cos \mathrm{A}\\[0.5em] &\large=&\large b^2 + c^2 -2 \hspace{1pt}b\hspace{1pt}c \cos \mathrm{A}\\ \end{eqnarray}
また、角\(\large{\mathrm{A}}\) が鋭角であり、点\(\large{\mathrm{C}}\) からの垂線の足\(\large{\mathrm{H}}\) が辺\(\large{\overline{\mathrm{AB}}}\) の外側にある場合は以下のようになります。
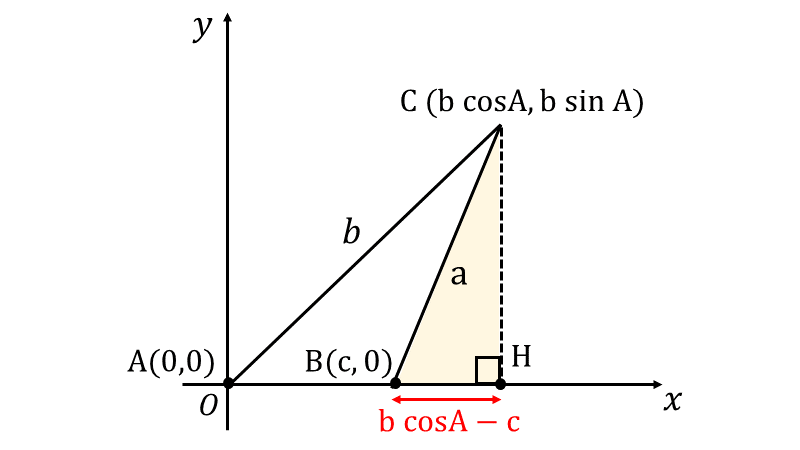
三角形\(\large{\mathrm{ C\hspace{1pt}H\hspace{1pt}B }}\) (図中の黄色部分) に着目し、三平方の定理を使用すると、以下のようになります。 $$\large{a^2= (b \sin \mathrm{A})^2 + (b \cos \mathrm{A} - c)^2}$$ 上式を整理すると、以下の式が成り立ちます。 $$\large{a^2 = b^2 + c^2 -2\hspace{1pt} b\hspace{1pt}c \cos \mathrm{A}}$$
したがって、角\(\large{\mathrm{A}}\) が鋭角である場合、余弦定理が成り立ちます。
・角Aが垂直である場合
角\(\large{\mathrm{A}}\)が垂直であれば、三角形\(\large{\mathrm{ A\hspace{1pt}B\hspace{1pt}C }}\) は下図のような直角三角形となります。

上図の直角三角形では、辺(\(\large{a,b,c}\)) に対して三平方の定理が成り立ちます。 $$\large{a^2 = b^2 + c^2}$$ このとき、角\(\large{\mathrm{A}}\) が垂直であることから、\(\large{\cos A = 0}\) となります。
したがって、角\(\large{\mathrm{A}}\) が垂直の場合も、以下の余弦定理が成立しています。 $$\large{a^2 = b^2 + c^2 -2\hspace{1pt} b\hspace{1pt}c \cos \mathrm{A}}$$
・角Aが鈍角である場合
角\(\large{\mathrm{A}}\) が鈍角である場合は、以下の図のようになります。

点\(\large{\mathrm{C}}\) から \(\large{x}\)軸への垂線の足\(\large{\mathrm{H}}\) は、辺\(\large{\overline{\mathrm{AB}}}\) の外側に位置します。
このとき、角度\(\large{\angle \mathrm{CAH}}\) は \(\large{180^\circ - \mathrm{A}}\) となります。
ここで、三角形\(\large{\mathrm{ C\hspace{1pt}A\hspace{1pt}H }}\) に対して \(\large{\angle \mathrm{CAH}=180^\circ - \mathrm{A}}\) の三角比を求めると、辺\(\large{\overline{\mathrm{CH}}}\) と \(\large{\overline{\mathrm{AH}}}\) の大きさが、以下のように求められます。 $$\large{\overline{\mathrm{CH}} = b \sin (180^\circ - \mathrm{A})}$$ $$\large{\overline{\mathrm{AH}} = b \cos (180^\circ - \mathrm{A})}$$
上式を三角比の180°-θの公式で変形すると、以下の式が求められます。 $$\large{\overline{\mathrm{CH}} = b \sin (180^\circ - \mathrm{A})=b \sin \mathrm{A}}$$ $$\large{\overline{\mathrm{AH}} = b \cos (180^\circ - \mathrm{A}) =- b \cos \mathrm{A}}$$
ここで、三角形\(\large{\mathrm{ C\hspace{1pt}H\hspace{1pt}B }}\) (図中の黄色部分) に三平方の定理を使用すると、以下のようになります。 \begin{eqnarray} \large a^2&\large=&\large (b \sin \mathrm{A})^2 + (c-b \cos \mathrm{A})^2 \\[0.5em] \large &\large=&\large b^2 (\sin^2 \mathrm{A} + \cos^2 \mathrm{A}) + c^2 -2 \hspace{1pt}b\hspace{1pt}c \cos \mathrm{A}\\[0.5em] &\large=&\large b^2 + c^2 -2\hspace{1pt} b\hspace{1pt}c \cos \mathrm{A}\\ \end{eqnarray}
よって、角\(\large{\mathrm{A}}\) が鈍角の場合も余弦定理が成り立つことが分かります。
以上から、角\(\large{\mathrm{A}}\) が鋭角、直角、鈍角のいずれの場合でも余弦定理 $$\large{a^2 = b^2 + c^2 -2 \hspace{1pt}b\hspace{1pt}c \cos \mathrm{A}}$$ が成立することが分かります。
また、上記の証明は角\(\large{\mathrm{B}}\)、角\(\large{\mathrm{C}}\) についても同様に成り立ちます。
【3】余弦定理の問題と解き方
三角比の余弦定理に関連した基礎的な問題を解説します。

問題(1)は 余弦定理を利用して三角形の辺の長さを求める問題です。

問題(2)は 余弦定理を利用して角度を求める問題です。
このとき、角\(\large{\angle \hspace{1pt}\mathrm{ BAC}}\) の角度 \(\large{\mathrm{A}}\) は 鋭角, 直角, 鈍角のいずれかであるか判定せよ。
問題(3)は 余弦定理を利用して角度が鋭角、直角、鈍角のどれかであるか判定する問題です。
問題(1) 三角形の辺の長さを求める問題

【解答と解説】
三角形\(\large{\mathrm{ A\hspace{1pt}B\hspace{1pt}C }}\) の2辺\(\large{\overline{\mathrm{AB}}}\)、\(\large{\overline{\mathrm{AC}}}\) と、辺\(\large{\overline{\mathrm{CB}}}\) の向かう合う角度\(\large{\mathrm{A}}\) が判明しているので、辺の長さ\(\large{a}\) は以下の余弦定理で求めることができます。
$$\large{a^2 = b^2 + c^2 -2 \hspace{1pt}b\hspace{1pt}c \cos \mathrm{A}}$$
余弦定理に値を入れると、以下のようになります。 \begin{eqnarray} \large a^2&\large=&\large 3^2+ 2^2 - 2 \times 3 \times 2 \cos 120^\circ\\ \large &\large=&\large 13 - 12 \times \left(-\frac{1}{2}\right)\\ \large &\large=&\large 19 \\ \end{eqnarray}
したがって、辺の長さ \(\large{a}\) は $$\large{a = \sqrt{19}}$$ と求められます。
問題(2) 三角形の角度を求める問題

【解答と解説】
三角形\(\large{\mathrm{ A\hspace{1pt}B\hspace{1pt}C }}\) の3辺の長さ (\(\large{a,b,c}\)) が判明しているので、角度\(\large{\mathrm{C}}\) は以下の余弦定理で求めることができます。
$$\large{\cos \mathrm{C} = \frac{a^2 + b^2 - c^2}{2 ab}}$$
余弦定理に値を入れると、以下のようになります。 \begin{eqnarray} \large \cos \mathrm{C}&\large=&\large \frac{(\sqrt{2})^2 + 3^2 - (\sqrt{5})^2}{2 \times \sqrt{2} \times 3}\\ \large &\large=&\large \frac{1}{\sqrt{2}}\\ \end{eqnarray}
したがって、角度\(\large{\mathrm{C}}\) は $$\large{\mathrm{C} = 45^\circ}$$ と求められます。
問題(3) 鋭角,直角,鈍角 を判定する問題
このとき、角\(\large{\angle \hspace{1pt}\mathrm{ BAC}}\) の角度 \(\large{\mathrm{A}}\) は 鋭角, 直角, 鈍角のいずれかであるか判定せよ。
【解答と解説】
角\(\large{\mathrm{A}}\) が鋭角、直角、鈍角のどれかは、余弦定理から \(\large{\cos \mathrm{A}}\) の値を求め、その符号を確認することで判定することができます。
| 角度A | 鋭角 | 直角 | 鈍角 |
|---|---|---|---|
| \(\large{\cos \mathrm{A}}\) の符号 |
\(\large{+}\) | \(\large{0}\) | \(\large{-}\) |
角\(\large{\mathrm{A}}\) に関する余弦定理は、以下となります。 $$\large{\cos \mathrm{A} = \frac{b^2 + c^2 - a^2}{2 \hspace{1pt}b\hspace{1pt}c}}$$ 上式から \(\large{\cos \mathrm{A}}\) の値を求めると、以下のように計算されます。 $$\large{\cos \mathrm{A} = \frac{7^2 + 8^2 - 3^2}{2 \times 7 \times 8} = \frac{104}{112}}$$ したがって、 $$\large{\cos \mathrm{A} > 0}$$
すなわち、\(\large{\cos \mathrm{A}}\) の値が正であるため、角\(\large{\mathrm{A}}\) は鋭角となります。
【別解】
計算を省略する方法として、余弦定理の分母 \(\large{2\hspace{1pt} b\hspace{1pt}c}\) は必ず正となるため、符号の判定は\(\large{b^2 + c^2 -a^2}\) のみで行うこともできます。
$$\large{b^2 + c^2 -a^2 = 104 >0}$$
より、\(\large{\cos \mathrm{A}}\) の値が正となるため、角\(\large{\mathrm{A}}\) は鋭角と分かります。
問題(4) 正弦定理と余弦定理を利用する問題
【解答と解説】
まず、辺の長さ\(\large{\hspace{2pt}a,\hspace{1pt}b\hspace{2pt}}\)と角度\(\large{\mathrm{\hspace{2pt}A,\hspace{1pt}B\hspace{2pt}}}\)に関する正弦定理
$$\large{\frac{a}{\sin \mathrm{A}} = \frac{b}{\sin \mathrm{B}}}$$
を利用して角\(\large{\mathrm{B}}\) の角度を求めます。
$$\large{\frac{2\sqrt{3}}{\sin 30°} = \frac{6}{\sin \mathrm{B}}}$$
$$\large{\displaystyle\sin \mathrm{B} = \frac{\sqrt{3}}{2}}$$
となります。
つまり、\(\large{0° < B < 180°}\) の範囲で \(\large{\displaystyle\sin \mathrm{B} = \frac{\sqrt{3}}{2}}\) を解くと、 $$\large{\mathrm{B} = 60°,\hspace{2pt}120°}$$ となります。
2つの角度を \(\large{\color{red}{\mathrm{B_1} = 60°}}\)、\(\large{\color{blue}{\mathrm{B_2} = 120°}}\) としたときの三角形を図にすると以下のようになります。

よって、角度\(\large{\mathrm{B}}\)の大きさによって場合分けして、残りの三角形の形状を求めます。
【Ⅰ】\(\large{\mathrm{B}=60°}\) のとき
角度\(\large{\mathrm{C}}\) は $$\large{C=180°-(30°+60°)=90°}$$ となります。
辺の長さ\(\large{c}\) は以下の余弦定理 $$\displaystyle\large{c^2 = a^2 + b^2 -2\hspace{1pt} ab \cos \mathrm{C}}$$ から、 \begin{eqnarray} \large c^2&\large =&\large (2\sqrt{3})^2+6^2 -2\cdot2\sqrt{3}\cdot6\cdot \cos90°\\[0.5em] \large &\large =&\large 48\\[0.5em] \end{eqnarray} ここで、\(\large{c>0}\) であるから $$\large{c=\sqrt{48}=4\sqrt{3}}$$ となります。
【Ⅱ】\(\large{\mathrm{B}=120°}\) のとき
角度\(\large{\mathrm{C}}\) は $$\large{\mathrm{C}=180°-(30°+120°)=30°}$$ となります。
辺の長さ\(\large{c}\) は以下の余弦定理 $$\displaystyle\large{c^2 = a^2 + b^2 -2\hspace{1pt} ab \cos \mathrm{C}}$$ から、 \begin{eqnarray} \large c^2&\large =&\large (2\sqrt{3})^2+6^2 -2\cdot2\sqrt{3}\cdot6\cdot \cos30°\\[0.5em] \large &\large =&\large 12\\[0.5em] \end{eqnarray} ここで、\(\large{c>0}\) であるから $$\large{c=\sqrt{12}=2\sqrt{3}}$$ となります。
したがって、求める辺の長さと角度は $$\large{c=4\sqrt{3}\hspace{1pt},\hspace{2pt}\mathrm{B}=60°\hspace{1pt},\hspace{2pt}\mathrm{C}=90°}$$ もしくは、 $$\large{c=2\sqrt{3}\hspace{1pt},\hspace{2pt}\mathrm{B}=120°\hspace{1pt},\hspace{2pt}\mathrm{C}=30°}$$ となります。
(問題4の別解)
辺\(\large{c}\) の長さは正弦定理から求めることもできます。
【Ⅰ】\(\large{B=60°}\) のとき
正弦定理 $$\large{\frac{a}{\sin \mathrm{A}} = \frac{c}{\sin \mathrm{C}}}$$ から、 $$\large{\frac{2\sqrt{3}}{\sin 30°} = \frac{c}{\sin 90°}}$$ $$\large{c=4\sqrt{3}}$$
【Ⅱ】\(\large{B=120°}\) のとき
正弦定理 $$\large{\frac{a}{\sin \mathrm{A}} = \frac{c}{\sin \mathrm{C}}}$$ から、 $$\large{\frac{2\sqrt{3}}{\sin 30°} = \frac{c}{\sin 30°}}$$ $$\large{c=2\sqrt{3}}$$ と求められます。