弧度法とは

本項では以下の内容を解説しています。

• ・弧度法の定義
• ・度数法 と 弧度法の変換式、値の一覧
• ・度数法、弧度法を変換する練習問題

【1】弧度法の定義

日常生活でもよく使用する \(\large{90°}\) や \(\large{180°}\) などの角度の表記を度数法といいます。
度数法では、円の一周を \(\large{360°}\) とすることで角度の大きさを表します。

一方、『 "円弧の長さ" と "円の半径" の比で角度を定義する方法』を弧度法といいます。

下図のように、半径 \(\large{r}\) の円に、円弧の長さ \(\large{l}\) をとります。この円弧に対する中心角を角度 \(\large{\theta}\) とします。

弧度法による角度\(\large{\theta}\) は、『円弧の長さ \(\large{\color{red}{\boldsymbol{l}}}\) 』 を 『円の半径 \(\large{\color{blue}{\boldsymbol{r}}}\) 』で割った値により表されます。

弧度法により表された角度の単位には、[rad] (ラジアン) を使用します。
通常、単位の[rad] は省略して表記されます。本項でも、以下の内容から[rad]を省略して表記します。

・角度180°のラジアン

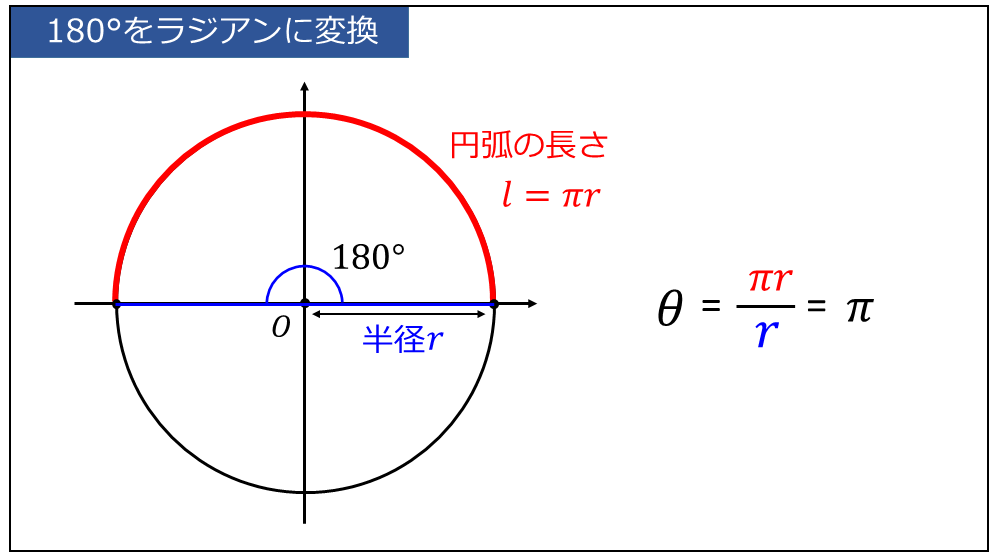
例えば、上記の弧度法の定義から、角度\(\large{180°}\) を弧度法で表記することを考えます。

半径\(\large{r}\) の円周の長さは、\(\large{2 \pi r}\) であるため、半円の円弧の長さは $$\large{l=\pi r}$$ となります。したがって、角度\(\large{180°}\) は弧度法の定義から $$\large{θ = \frac{l}{r}=\frac{\pi r}{r}=\pi}$$ となります。

・角度90°のラジアン

また、角度\(\large{90°}\) を弧度法で表記する場合を考えます。

半径\(\large{r}\) の円周の長さは、\(\large{2 \pi r}\) であるため、円周の \(\displaystyle \large{\frac{1}{4}}\) の長さは $$\large{l=\frac{\pi r}{2}}$$ であるため、角度\(\large{90°}\) は弧度法の定義から $$\large{\theta =\frac{l}{r}= \frac{\pi r}{2}\times \frac{1}{r} = \frac{\pi}{2}}$$ となります。

上記の計算からも分かるように、角度を弧度法により表記すると、円の半径\(\large{r}\) に関わらず一定の値となります。通常、弧度法は半径 \(\large{r=1}\) の円(単位円)で定義されます。

・1ラジアン と 1°の大きさ

先ほどの計算結果から、角度 \(\large{180°}\) は、弧度法の \(\large{\pi}\) と一致します。 $$\large{180° = \pi \hspace{10pt}(1)}$$

(1)式の両辺を \(\large{180}\) で割ることで、1°に等しい角度[rad]を求められます。

一方、(1)式の両辺を \(\large{\pi}\) で割ることで、1ラジアンに等しい角度[°]を求められます。

(2),(3)式を利用することで、角度の単位[°]と[rad]を変換する式を得ることができます。

また、弧度法の定義から、1ラジアンの角度は、半径1の円において 円弧の長さが1となる角度であることを意味します。

【2】弧度法と度数法の変換式

本章では、弧度法[rad] と 度数法[°] を変換する式と、変換の具体例について解説します。

・度数法から弧度法への変換

前章で示したように、角度1°あたりのラジアンの値は $$\large{1° = \frac{\pi}{180}}$$ となります。

したがって、ある角度 \(\large{\theta°}\)を弧度法で表すときは、上式の両辺に \(\large{\theta}\) をかけて \(\large{\theta°}\) あたりのラジアンとすれば、以下の変換式が求めれられます。

例えば、\(\large{\theta=90°}\) を弧度法で表すと、以下のようになります。 $$\large{90° = 90 \times \frac{\pi}{180} = \frac{\pi}{2}}$$

・弧度法から度数法への変換

また、弧度法で表された角度\(\large{\theta\hspace{1pt}}\)[rad] を度数法で表す場合は、以下のように計算します。

例えば、\(\large{\displaystyle \theta=\frac{\pi}{2}}\) を度数法で表すと、以下のようになります。 $$\large{\frac{\pi}{2} = \frac{\pi}{2} \times \frac{180}{\pi}° = 90°}$$

後述する【4】変換の問題で 弧度法と度数法を変換する計算例を紹介しています。

【3】弧度法 と 度数法 の一覧

前章の弧度法と度数法の変換式を利用することで、一覧表を作ることができます。
以下の表に、度数法[°] と 弧度法[rad] の一覧を示します。

【4】度数法 と 弧度法 の変換の問題

本章では、弧度法と度数法を変換する問題について解説します。

【4-1】度数法 ⇒ 弧度法 に変換

・問題(1)
度数法と弧度法を変換する式から、 $$\large{20° = 20 \times \frac{\pi}{180} = \frac{\pi}{9}}$$ となります。

・問題(2)
問題(1)と同様の式で変換すると、 $$\large{720° = 720 \times \frac{\pi}{180} = 4 \pi}$$ となります。

・問題(3)
問題(1)と同様の式で変換すると、 $$\large{-120° = -120 \times \frac{\pi}{180} = -\frac{2}{3}\pi}$$ となります。

【4-2】弧度法 ⇒ 度数法に変換

・問題(4)
弧度法と度数法を変換する式から、 $$\large{\frac{9}{10}\pi =\frac{9}{10}\pi \times \frac{180}{\pi} ° = 162°}$$ となります。

・問題(5)
問題(4)と同様の式で変換すると、 $$\large{\frac{7}{5}\pi =\frac{7}{5}\pi \times \frac{180}{\pi} ° = 252°}$$ となります。

・問題(6)
問題(4)と同様の式で変換すると、 $$\large{3 \pi = 3 \pi \times \frac{180}{\pi} ° = 540°}$$ となります。

---