余弦定理の計算ツール
本計算ツールは 余弦定理 から 三角形の辺の長さ、角度を計算する計算機です。
以下の ① または ② から、他の辺の長さと角度を求めます。
・『① 2辺の長さ と 2辺の間の角度』
・『② 3辺の長さ』
①『2辺の長さと間の角度』から計算
『2辺の長さ(b,c), 角度(∠A)』 から 『辺BCの長さ(a), 角度(∠B,∠C)』を計算します。
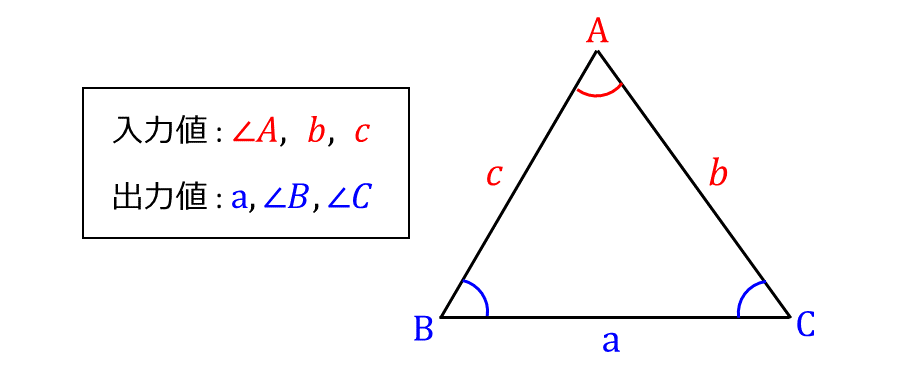
以下の(1)~(3)の手順で実行してください。
(1) "角度の入力単位"から『 度数法[°] 』か『 弧度法[rad] 』を選択
(2) 計算する角度∠A、2辺の長さ(b,c)を入力
(3)『計算実行』を押して実行
【角度と2辺の長さの入力】
:
角度 : ∠A =
辺AC の長さ : b =
辺AB の長さ : c =
【出力値の設定】
出力値の小数点以下の桁数 :
| 辺BCの長さ(a) | |
|---|---|
| 角度∠B | |
| 角度∠C |
【弧度法[rad]の入力方法】
1. 円周率\(\large{\pi}\)を 半角英字"pi"で入力
2. 半角数字 x,y を使用して
"xpi", "pi/x", "x/ypi"で入力
入力例 : \(\large{\frac{1}{4}\pi}\) ⇒ 『pi/4』,『1/4pi』
\(\large{\frac{3}{4}\pi}\) ⇒ 『3/4pi』
②『3辺の長さ』から計算
『3辺の長さ(a,b,c)』 から 『角度(∠A,∠B,∠C)』を計算します。

以下の(1)~(3)の手順で実行してください。
(1)計算する3辺の長さ(a,b,c)を入力
(2)"角度の単位"から『 度数法[°] 』か『 弧度法[rad] 』を選択
(3)『計算実行』を押して実行
【3辺の長さの入力】
辺BC の長さ a =
辺AC の長さ : b =
辺AB の長さ : c =
【出力値の設定】
:
出力値の小数点以下の桁数 :
| 角度∠A | |
|---|---|
| 角度∠B | |
| 角度∠C |
計算ツールの説明
本計算ツールについて説明します。
余弦定理による計算方法
余弦定理とは、三角形\(\large{ABC}\) の辺の長さ (\(\large{a,b,c}\)) と、角度 (\(\large{A,B,C}\)) に対して成り立つ等式のことをいいます。
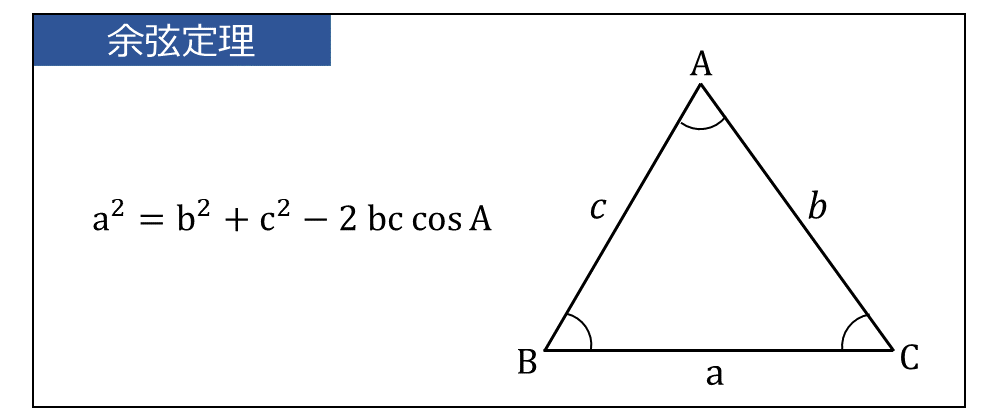
上図に示す三角形\(\large{ABC}\) において、辺\(\large{\overline{BC}}\) の長さ\(\large{a}\) を求める余弦定理は、 $$\displaystyle\large{a^2 = b^2 + c^2 -2\hspace{1pt} b\hspace{1pt}c \cos A}$$ と表されます。
また、辺\(\large{\overline{AC}}\) の長さ\(\large{b}\)、辺\(\large{\overline{AB}}\) の長さ\(\large{c}\) を求める場合、以下のような式となります。 $$\displaystyle\large{b^2 = c^2 + a^2 -2\hspace{1pt} c\hspace{1pt}a \cos B}$$ $$\displaystyle\large{c^2 = a^2 + b^2 -2\hspace{1pt} a\hspace{1pt}b \cos C}$$
本計算ツールでは、上式から辺の長さを計算します。
また、3辺の長さ (\(\large{a,b,c}\)) が分かる場合、以下のように余弦定理を変形し、角度 (\(\large{A,B,C}\)) を計算できます。 $$\large{\cos A = \frac{b^2 + c^2 - a^2}{2\hspace{1pt} bc}}$$ $$\large{\cos B = \frac{a^2 + c^2 - b^2}{2 ac}}$$ $$\large{\cos C = \frac{a^2 + b^2 - c^2}{2 ab}}$$ 本計算ツールでは、上式から三角形のそれぞれの角度を計算しています。
出力値の設定
『出力値の小数点以下の桁数』では、入力された桁より1つ小さい桁で出力値を四捨五入します。
(例)『出力値の小数点以下の桁数』が2 → 出力が『0.59284...』の場合は、小数点以下3桁で四捨五入して『0.59』となります。