三角比の定義
本項では、『三角比の定義と覚え方』、『30°、45°、60°の三角比』 について解説しています。
【1】三角比の定義
三角比とは、直角三角形の3辺の比から定義される正弦(サイン)、余弦(コサイン)、正接(タンジェント)の3つの値のことをいいます。
下図のような直角三角形ABCにおいて、\(\large{\angle }\)BAC\(\large{=\theta}\)としたとき、正接(\(\large{\boldsymbol \sin \theta}\))、余弦(\(\large{\boldsymbol \cos \theta}\))、正接(\(\large{\boldsymbol \tan \theta}\))は以下のように定義されます。

・三角比の定義の覚え方
三角比の定義の覚え方として、『サイン、コサイン、タンジェントの頭文字(s,c,t)の筆記体』と、『三角比の割り算の分母、分子』を対応させる覚え方があります。

直角三角形の角度\(\large{\theta}\)を左側、直角を右側に見たときに、『サインは"s"の筆記体から、斜辺を分母、高さを分子』と定義されると覚えます。
同様に、『コサインは"c"の筆記体から、斜辺を分母、底辺を分子』、『タンジェントは"t"の筆記体から、底辺を分母、高さを分子』と覚えます。
【2】角度30°,45°,60°の三角比
よく使用される角度が30°, 45°, 60°の三角比の値について解説します。
・角度が30°の三角比
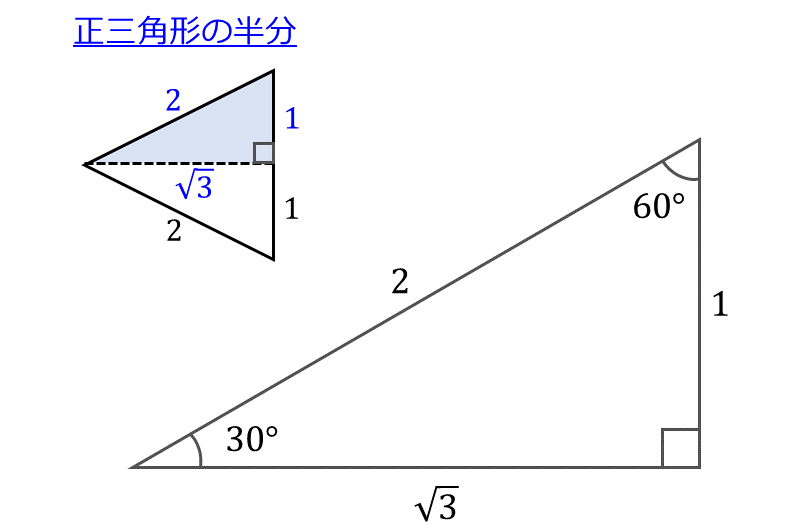
下図のように、1辺の大きさが 2 の正三角形を半分にすると、角度30°を持つ直角三角形とすることができます。
三平方の定理から、この直角三角形の3辺は『斜辺が\(\large{\hspace{2pt} 2 \hspace{2pt}}\)、底辺が\(\large{\hspace{2pt} \sqrt{3} \hspace{2pt}}\)、高さが\(\large{\hspace{2pt} 1 \hspace{2pt}}\)』となります。
直角三角形の3辺の大きさが分かれば、三角比の定義からsin、cos、tanの値を求めることができます。
三角比の定義から、角度30°のsin、cos、tanの値は以下のように求められます。 $$\large{\sin 30^\circ = \frac{1}{2}}$$ $$\large{\cos 30^\circ = \frac{\sqrt{3}}{2}}$$ $$\large{\tan 30^\circ = \frac{1}{\sqrt{3}}}$$
・角度が45°の三角比
1辺の大きさが1の正方形を半分にすると、角度45°を持つ直角三角形とすることができます。
三平方の定理から、この直角三角形の3辺は『斜辺が\(\large{\hspace{2pt}\sqrt{2}\hspace{2pt}}\)、底辺が\(\large{\hspace{2pt} 1 \hspace{2pt}}\)、高さが\(\large{\hspace{2pt} 1 \hspace{2pt}}\)』となります。

三角比の定義から、角度45°のsin、cos、tanの値は以下のように求められます。 \begin{eqnarray} \large \sin 45^\circ&\large =&\large \frac{1}{\sqrt{2}}\\ \large \cos 45^\circ&\large =&\large \frac{1}{\sqrt{2}}\\ \large \tan 45^\circ&\large =&\large 1\\ \end{eqnarray}
・角度が60°の三角比
1辺の大きさが2の正三角形を半分にすると、角度60°を持つ直角三角形とすることができます。(30°の直角三角形を回転させた三角形です。)
三平方の定理から、この直角三角形の3辺は『斜辺が\(\large{\hspace{2pt} 2 \hspace{2pt}}\)、底辺が\(\large{\hspace{2pt} 1 \hspace{2pt}}\)、高さが\(\large{\hspace{2pt} \sqrt{3} \hspace{2pt}}\)』となります。

三角比の定義から、角度60°のsin、cos、tanの値は以下のように求められます。 $$\large{\sin 60^\circ = \frac{\sqrt{3}}{2}}$$ $$\large{\cos 60^\circ = \frac{1}{2}}$$ $$\large{\tan 60^\circ = \sqrt{3}}$$
・角度30°、45°、60°の三角比一覧
以下の表に角度が30°、45°、60°のときのサイン、コサイン、タンジェントの一覧を示します。
| 角度 | \(\large{30^\circ}\) | \(\large{45^\circ}\) | \(\large{60^\circ}\) |
|---|---|---|---|
| \(\displaystyle \large{\sin \theta}\) | \(\displaystyle \large{\frac{1}{2}}\) | \(\displaystyle \large{\frac{1}{\sqrt{2}}}\) | \(\displaystyle \large{\frac{\sqrt{3}}{2}}\) |
| \(\displaystyle \large{\cos \theta}\) | \(\displaystyle \large{\frac{\sqrt{3}}{2}}\) | \(\displaystyle \large{\frac{1}{\sqrt{2}}}\) | \(\displaystyle \large{\frac{1}{2}}\) |
| \(\displaystyle \large{\tan \theta}\) | \(\displaystyle \large{\frac{1}{\sqrt{3}}}\) | \(\displaystyle \large{1}\) | \(\displaystyle \large{\sqrt{3}}\) |