三角比の正弦定理

【1】正弦定理の意味と使い方

下図のような辺の長さ (\(\large{a,b,c}\)) を持つ三角形 \(\large{ABC}\) に対し、その外接円の半径が \(\large{R}\) であるとき、以下の式で表される正弦定理が成り立ちます。

辺の長さ (\(\large{a,b,c}\)) と角度 (\(\large{A, B, C}\)) で構成される以下の式は、三角形の辺の比と、辺に向かい合う角度の比が等しいことを意味します。 $$\large{\frac{a}{\sin A} = \frac{b}{\sin B}=\frac{c}{\sin C}}$$ 上式を比で表すと以下のようになります。 $$\large{a:b:c=\sin A:\sin B:\sin C}$$

・正弦定理の使い方

正弦定理は、三角形の形状(辺や角度の大きさ)を求める問題によく使用されます。

式中には、4つの項が存在しますが、問題に応じて必要な項を使用します。
例えば、角度 \(\large{A}\)、外接円の半径 \(\large{R}\) から辺の長さ \(\large{a}\) を求める場合は、 $$\large{\frac{a}{\sin A} = 2R}$$ を使用します。

また、辺の長さ \(\large{a}\)、角度 \(\large{A}\)、角度 \(\large{B}\) から、辺の長さ \(\large{b}\) を求める場合は、 $$\large{\frac{a}{\sin A} = \frac{b}{\sin B}}$$ から求めることができます。

後述する練習問題では、正弦定理を使用し三角形の形状を求める問題について解説しています。

【2】正弦定理の証明

本章では、正弦定理の証明について解説します。

正弦定理の証明には、円周角の定理を使用します。まず、円周角の定理について解説し、その後、正弦定理の証明を行います。

【証明の準備】円周角の定理

正弦定理の証明には、円周角の定理を使用します。

円周角の定理は、円弧を共通している円周角は一定となるという関係を説明する定理です。例えば、下図のように円の孤 \(\large{BC}\) を共通している場合、その円周角 \(\large{A}\)、\(\large{A'}\) は一定となります。

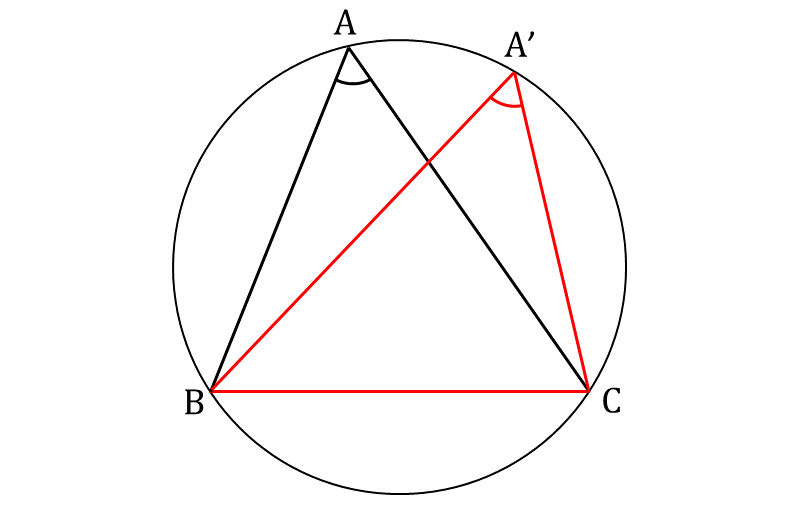
また、下図のように \(\large{BC}\) を結ぶ直線が円の中心 \(\large{O}\) を通る場合、その円周角 \(\large{A}\) は \(\large{90^\circ}\) となります。

・正弦定理の証明 | 鋭角の場合

上記の円周角の定理を使用して、正弦定理を証明します。

正弦定理を使用した証明では、対象となる角度が鋭角、直角、鈍角で証明方法が異なるため、場合分けして証明します。

まず、角度\(\large{A}\) が鋭角である場合に、\(\large{\displaystyle \frac{a}{\sin A}=2R}\) が成り立つことを説明します。

(辺\(\large{a}\) と角度\(\large{A}\) に関する式 \(\large{\displaystyle \frac{a}{\sin A}=2R}\) が成り立つことを証明できれば、辺\(\large{b,c}\) と角度 \(\large{B,C}\) についても同様に導くことができます。)

下図のように、三角形\(\large{ABC}\) の外接円の半径が \(\large{2R}\) であるとします。
このとき、共通の辺 \(\large{BC}\) を持ち、辺 \(\large{A'B}\) が外接円の中心を通るような三角形\(\large{A'BC}\) を考えます。

このとき、中心角の定理から、辺 \(\large{A'B}\) の円周角は \(\large{\angle A'CB=90^\circ}\) となります。

三角形\(\large{A'BC}\) の角度\(\large{A'}\) 対して、\(\large{\sin A'}\) を求めると、以下のようになります。 $$\large{\sin A' = \frac{a}{2R}}$$

ここで、円周角の定理から、辺 \(\large{BC}\) を共有している角度\(\large{A}\) と角度\(\large{A'}\) は等しい値になります。したがって、以下の式が成り立ちます。 $$\large{\sin A = \frac{a}{2R}}$$

・正弦定理の証明 | 直角の場合

次に、角度\(\large{A}\) が直角である場合に、\(\large{\displaystyle \frac{a}{\sin A}=2R}\) が成り立つことを説明します。

下図のように、角度 \(\large{A}\) が直角である場合、外接円の定理から、三角形 \(\large{ABC}\) の辺 \(\large{BC}\) が半径 \(\large{R}\) の外接円の中心を通ります。

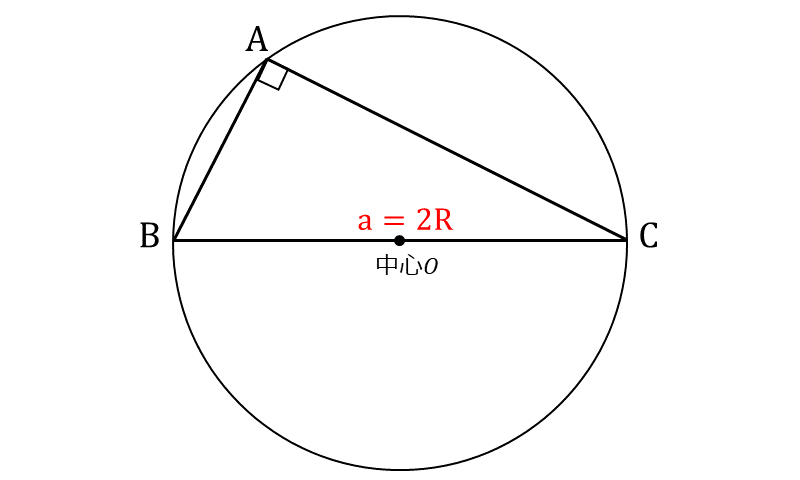
このとき、\(\large{ A = 90^\circ}\) より、\(\large{\sin A = 1}\) となります。
また、上図より \(\large{a = 2R}\) であるため、以下の式が成り立ちます。 $$\large{\sin A = \frac{a}{2R}}$$

・正弦定理の証明 | 鈍角の場合

次に、角度 \(\large{A}\) が鈍角である場合に、\(\displaystyle \large{\frac{a}{\sin A}=2R}\) が成り立つことを説明します。

下図のように、辺\(\large{A'C}\) が外接円の中心を通るような点\(\large{A'}\) を考えます。

このとき、円周角の定理より、辺 \(\large{A'C}\)が円の中心を通ることから、\(\large{\angle A'BC = 90^\circ}\) となります。

したがって、三角形\(\large{A'BC}\) の角度\(\large{A'}\) の三角比を求めると、以下のようになります。 $$\large{\sin A' = \frac{a}{2R}}$$

円に内接する四角形の向かい合った角の角度の和は \(\large{180^\circ}\) であるという性質を用いると、角度\(\large{A}\) と角度\(\large{A'}\) に関して以下の式が成り立ちます。 $$\large{A + A' = 180^\circ}$$

したがって、三角比の180°-θを変換する公式から、\(\large{\sin A'}\) は以下のように変形されます。 $$\large{\sin A' = \sin (180^\circ - A) = \sin A}$$

以上より、以下の式が導かれます。 $$\large{\sin A = \frac{a}{2R}}$$

【3】三角比の正弦定理の練習問題

三角比の正弦定理に関連した問題を解説します。

【解答と解説】
以下の正弦定理を必要な箇所だけを抜き出して、辺と角度を求めていきます。
$$\large{\frac{a}{\sin A} = \frac{b}{\sin B}=\frac{c}{\sin C}=2R}$$

【辺の長さ\(\large{a}\)】

まず、辺の長さ \(\large{a}\) を求めます。正弦定理から、辺の長さ \(\large{a}\) について以下が成り立ちます。 $$\large{\frac{a}{\sin A} =2R}$$

したがって、辺の長さ \(\large{a}\) は以下のように求められます。 $$\large{a = 2R \sin A = 6 \sin 60^\circ = 3 \sqrt{3}}$$

【角度\(\large{C}\)】
角度\(\large{C}\) は三角形の内角の和が \(\large{180^\circ}\) であることから、以下のように求められます。 $$\large{60^\circ + 75^\circ + C = 180^\circ}$$ $$\large{ C = 45^\circ}$$

【辺の長さ\(\large{c}\)】
次に、辺の長さ \(\large{c}\) は、正弦定理から辺の長さ \(\large{c}\) について以下が成り立つことから求めます。 $$\large{\frac{c}{\sin C} =2R}$$

したがって、辺の長さ \(\large{c}\) は以下のように求められます。 $$\large{c = 2R \sin C = 6 \sin 45^\circ =3 \sqrt{2}}$$

---