対数関数の最大値・最小値(置き換え型)
本項では以下の内容を解説しています。
- ・対数関数の最大最小の求め方
- ・関連する問題
【1】対数関数の最大値・最小値の解き方
変数の置き換えを使用する対数関数の最大値・最小値の問題の解き方を解説します。
【1-1】対数関数の二乗の項が含まれる問題
本章では、基本的な対数関数の二乗の項が含まれる問題の解き方を解説します。
\(\large{y=(\log_2 x)^2 - 2 \log_2 x + 3\hspace{4pt}}\)のように対数を二乗した項が含まれる関数の最大値・最小値は $$\large{\log_2 x = t}$$ と別の変数に置き換えて二次関数の問題として解きます。
対数関数の二乗の項が含まれる場合は以下のような手順で解きます。
2. \(\large{\log_{\hspace{1pt}a} x = t\hspace{2pt}}\)と置き換える
3. 変数\(\large{ \hspace{1pt}t\hspace{2pt}}\)の範囲を求める
4. \(\large{t\hspace{2pt}}\)の二次関数の最大値・最小値を求める
5. \(\large{x = a^t\hspace{2pt}}\)から最大値・最小値となる\(\large{\hspace{1pt}t\hspace{2pt}}\)を\(\large{\hspace{1pt}x\hspace{2pt}}\)に戻す
【1-2】例題
\(\large{\hspace{5pt}y=(\log_2 x)^2 - 2 \log_2 x + 3}\)
例題のような関数は $$\large{\log_2 x = t}$$ とおくことで\(\large{\hspace{2pt}t\hspace{3pt}}\)に関する二次関数の最大値・最小値の問題として解くことができます。
まず、真数条件は\(\large{\hspace{2pt}x\hspace{2pt}}\)の定義域が\(\large{\hspace{1pt}1 \leqq x \leqq 16\hspace{3pt}}\)であるため、真数条件\(\large{\hspace{1pt}x>0\hspace{2pt}}\)を満たします。
次に\(\large{\hspace{3pt}\log_2 x = t\hspace{2pt}}\)と置き換えたときの\(\large{\hspace{2pt}t\hspace{3pt}}\)の範囲を求めると $$\large{1 \leqq x \leqq 16}$$ から $$\large{\log_2 1 \leqq \log_2 x \leqq \log_2 16}$$ すなわち $$\large{0 \leqq t \leqq 4}$$ となります。
問題の関数を\(\large{\hspace{1pt}t\hspace{2pt}}\)を用いて表すと \begin{eqnarray} \large y &\large =&\large t^2 - 2 t + 3\\[0.7em] \large &\large =&\large (t-1)^2+2 \\[0.7em] \\[0.7em] \end{eqnarray}
上式のグラフを描くと以下のようになります。
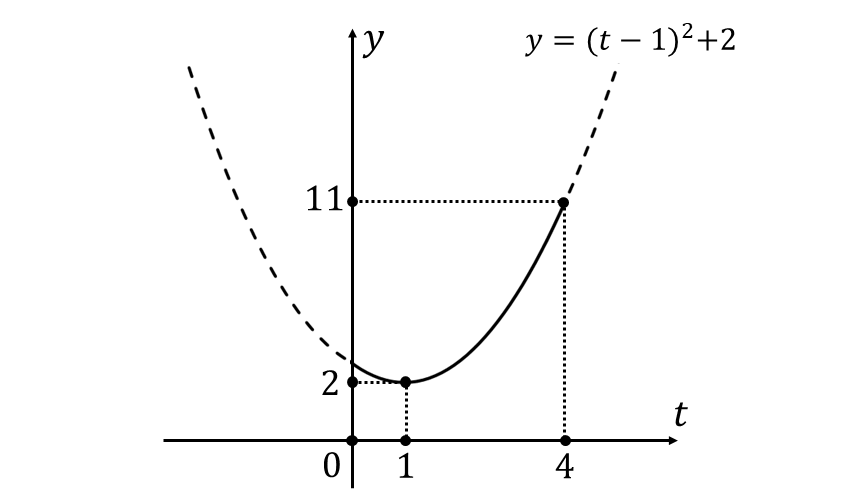
上図から\(\large{\hspace{3pt}t=4\hspace{2pt}}\)のとき最大値\(\large{\hspace{1pt}11\hspace{2pt}}\)、\(\large{\hspace{1pt}t=1\hspace{2pt}}\)のとき最小値\(\large{\hspace{1pt}2\hspace{2pt}}\)をとります。
ここで、最大値・最小値となる変数\(\large{\hspace{1pt}t\hspace{2pt}}\)を\(\large{\hspace{1pt}x\hspace{2pt}}\)に戻します。
\(\large{\log_2 x = t\hspace{3pt}}\)すなわち\(\large{\hspace{3pt}x=2^t\hspace{3pt}}\)から変形すると
\(\large{t=4\hspace{2pt}}\)であるとき\(\large{\hspace{3pt}x=2^4 \hspace{3pt}}\)よって\(\large{\hspace{2pt}x=16\hspace{2pt}}\)
\(\large{t=1\hspace{2pt}}\)であるとき\(\large{\hspace{3pt}x=2^1\hspace{3pt}}\)よって\(\large{\hspace{2pt}x=2\hspace{2pt}}\)
となります。
したがって、問題の関数は
\(\large{x=16\hspace{3pt}}\)のとき最大値\(\large{\hspace{1pt}11\hspace{2pt}}\)
\(\large{x=2\hspace{3pt}}\)のとき最小値\(\large{\hspace{1pt}2\hspace{2pt}}\)
と求められます。
【2】問題の一覧と解き方
対数関数の最大値・最小値を変数の置き換えにより求める問題には、いくつかのパターンがあります。
本章では、変数の置き換えを利用するの問題の一覧と解き方を解説します。
\(\large{\hspace{5pt}y=\log_2 \hspace{1pt}(-x^2+8x)}\)
解答と解説 : 問題1
\(\large{\hspace{5pt}y=\log_\frac{1}{2} \hspace{1pt}(-x^2-4x-3)}\)
解答と解説 : 問題2
\(\displaystyle\large{\hspace{5pt}y=\left(\log_3 \hspace{1pt}\frac{x}{3}\right)\left(\log_3 \hspace{1pt}\frac{9}{x}\right)}\)
解答と解説 : 問題3
\(\displaystyle\large{z=(\log_2 \hspace{1pt}x)\hspace{1pt}(\log_2 \hspace{1pt}y)}\)
の最大値・最小値を求めよ
解答と解説 : 問題4
・問題1 | 真数がxの二次式の場合
\(\large{\hspace{5pt}y=\log_2 \hspace{1pt}(-x^2+8x)}\)
この問題は、対数関数の真数が\(\large{\hspace{1pt}x\hspace{2pt}}\)の二次式となっています。
そこで\(\large{\hspace{2pt}t=-x^2+8x\hspace{2pt}}\)とおき、まず真数\(\large{\hspace{1pt}t\hspace{2pt}}\)の最大値・最小値を求めます。
真数条件から $$\large{-x^2+8x > 0}$$ すなわち $$\large{-x(x-8) > 0}$$ よって $$\large{0 < x < 8}$$ となります。
\(\large{t=-x^2+8x\hspace{2pt}}\)を平方完成すると \begin{eqnarray} \large t &\large =&\large -x^2+8x\\[0.7em] \large &\large =&\large -(x-4)^2+16 \\[0.7em] \\[0.7em] \end{eqnarray} となります。
上式のグラフを描くと以下のようになります。
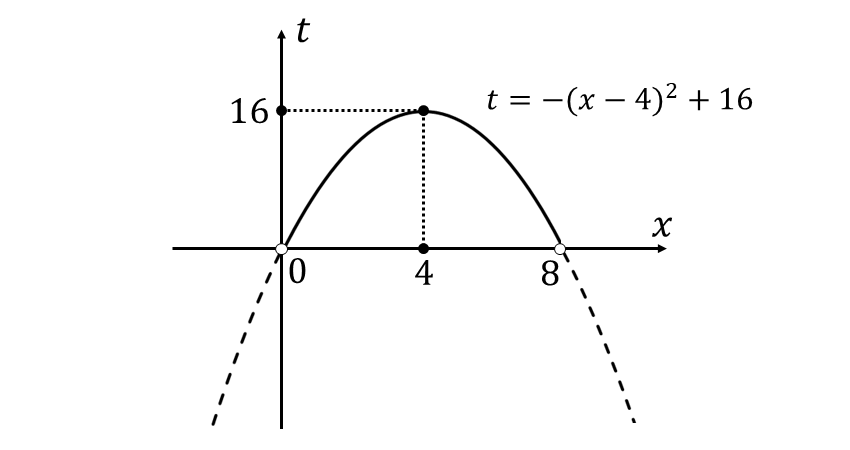
上図から\(\large{\hspace{3pt}x=4\hspace{2pt}}\)のとき、真数\(\large{\hspace{1pt}t\hspace{2pt}}\)の最大値は\(\large{\hspace{1pt}16\hspace{2pt}}\)、最小値はなしとなります。
ここで、底が\(\large{\hspace{1pt}1\hspace{2pt}}\)より大きいため、問題の対数関数は単調増加(\(\large{\hspace{1pt}x\hspace{2pt}}\)が増加すると\(\large{\hspace{1pt}y\hspace{2pt}}\)が増加する)となります。
この場合、真数が最大値となる\(\large{\hspace{1pt}x\hspace{2pt}}\)において対数関数は最大値、真数が最小値となる\(\large{\hspace{1pt}x\hspace{2pt}}\)において対数関数は最小値となります。
\(\large{x=4\hspace{2pt}}\)であるとき、問題の関数の値は
\begin{eqnarray}
\large
y &\large =&\large \log_2 16\\[0.7em]
\large
&\large =&\large \log_2 2^4 \\[0.7em]
\large
&\large =&\large 4 \\[0.7em]
\\[0.7em]
\end{eqnarray}
したがって、問題の関数は
\(\large{x=4\hspace{3pt}}\)のとき最大値\(\large{\hspace{1pt}4\hspace{2pt}}\)
最小値はなし
と求められます。
・問題2 | 底が1より小さい場合の最大値・最小値
\(\large{\hspace{5pt}y=\log_\frac{1}{2} \hspace{1pt}(-x^2-4x-3)}\)
この問題は、問題1と同様に対数関数の真数が\(\large{\hspace{1pt}x\hspace{2pt}}\)の二次式となっています。
問題1との違いは対数関数の底が\(\large{\hspace{1pt}1\hspace{2pt}}\)より小さいため、対数関数が単調減少(\(\large{\hspace{1pt}x\hspace{2pt}}\)が増加すると\(\large{\hspace{1pt}y\hspace{2pt}}\)が減少する)であるという点にあります。
この場合、真数が最大値となる\(\large{\hspace{1pt}x\hspace{2pt}}\)において対数関数は最小値、真数が最小値となる\(\large{\hspace{1pt}x\hspace{2pt}}\)において対数関数は最大値となります。
本問は、対数関数の真数が\(\large{\hspace{1pt}x\hspace{2pt}}\)の二次式となっているため、\(\large{t=-x^2-4x-3\hspace{2pt}}\)とおき、真数\(\large{\hspace{1pt}t\hspace{2pt}}\)の最大値・最小値を求めます。
まず真数条件から $$\large{-x^2-4x-3 > 0}$$ すなわち $$\large{(x+1)(x+3) < 0}$$ よって $$\large{-1 < x < -3}$$ となります。
\(\large{t=-x^2-4x-3\hspace{2pt}}\)を平方完成すると \begin{eqnarray} \large t &\large =&\large -x^2-4x-3\\[0.7em] \large &\large =&\large -(x^2+4x)-3 \\[0.7em] \large &\large =&\large -(x+2)^2+1 \\[0.7em] \\[0.7em] \end{eqnarray} となります。
上式のグラフを描くと以下のようになります。
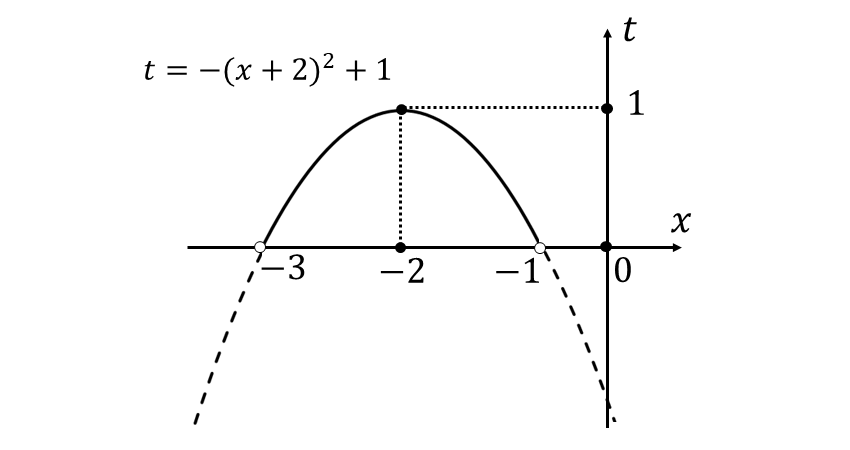
上図から\(\large{\hspace{3pt}x=-2\hspace{2pt}}\)のとき真数\(\large{\hspace{1pt}t\hspace{2pt}}\)の最大値は\(\large{\hspace{1pt}1\hspace{2pt}}\)、最小値はなしとなります。
ここで\(\large{\hspace{3pt}x=-2\hspace{3pt}}\)であるとき、問題の関数の値は
\begin{eqnarray}
\large
y &\large =&\large \log_\frac{1}{2} 1\\[0.7em]
\large
&\large =&\large 0\\[0.7em]
\\[0.7em]
\end{eqnarray}
となります。
対数関数の底が\(\large{\hspace{1pt}1\hspace{2pt}}\)より小さいため、真数が最大値となる\(\large{\hspace{1pt}x\hspace{2pt}}\)において対数関数は最小値、真数が最小値となる\(\large{\hspace{1pt}x\hspace{2pt}}\)において対数関数は最大値となります。
したがって、問題の関数は
最大値はなし
\(\large{x=-2\hspace{3pt}}\)のとき最小値は\(\large{\hspace{2pt}0}\)
と求められます。
・問題3 | 対数の公式から変形する問題
\(\displaystyle\large{\hspace{5pt}y=\left(\log_3 \hspace{1pt}\frac{x}{3}\right)\left(\log_3 \hspace{1pt}\frac{9}{x}\right)}\)
まず、\(\large{x\hspace{2pt}}\)の定義域は\(\large{1 \leqq x \leqq 9\hspace{2pt}}\)であるため、真数条件\(\displaystyle\large{\hspace{4pt}\frac{x}{3}>0\hspace{2pt},}\)\(\displaystyle\large{\hspace{2pt}\frac{9}{x}>0\hspace{4pt}}\)を満たします。
次に問題の関数を対数の公式
$$\large{\log_a \frac{M}{N} = \log_a M - \log_a N}$$
から変形します。
\(\displaystyle\large{y=\left(\log_3 \hspace{1pt}\frac{x}{3}\right)\left(\log_3 \hspace{1pt}\frac{9}{x}\right)\hspace{2pt}}\)を変形すると \begin{eqnarray} \large y &\large =&\large \left(\log_3 \hspace{1pt}\frac{x}{3}\right)\left(\log_3 \hspace{1pt}\frac{9}{x}\right)\\[0.7em] \large &\large =&\large \left(\log_3 x - \log_3 3\right)\left(\log_3 9 - \log_3 x \right) \\[0.7em] \large &\large =&\large \left(\log_3 x -1 \right)\left(2 - \log_3 x \right) \\[0.7em] \large &\large =&\large -(\log_3 x)^2 +3 \log_3 x-2 \\[0.7em] \\[0.7em] \end{eqnarray}
ここで\(\large{\hspace{3pt}\log_3 x = t\hspace{3pt}}\)とおくと、\(\large{x\hspace{2pt}}\)の範囲が\(\large{\hspace{2pt}1 \leqq x \leqq 9\hspace{4pt}}\)であることから、 $$\large{\log_3 1 \leqq \log_3 x \leqq \log_3 9}$$ すなわち $$\large{0 \leqq t \leqq 2}$$ となります。
\(\large{y=-t^2+3t-2\hspace{2pt}}\)を平方完成すると \begin{eqnarray} \large y &\large =&\large -(t^2-3t)-2\\[0.7em] \large &\large =&\large -\left(t-\frac{3}{2}\right)^2 +\frac{1}{4}\\[0.7em] \\[0.7em] \end{eqnarray} となります。
上式のグラフを描くと以下のようになります。
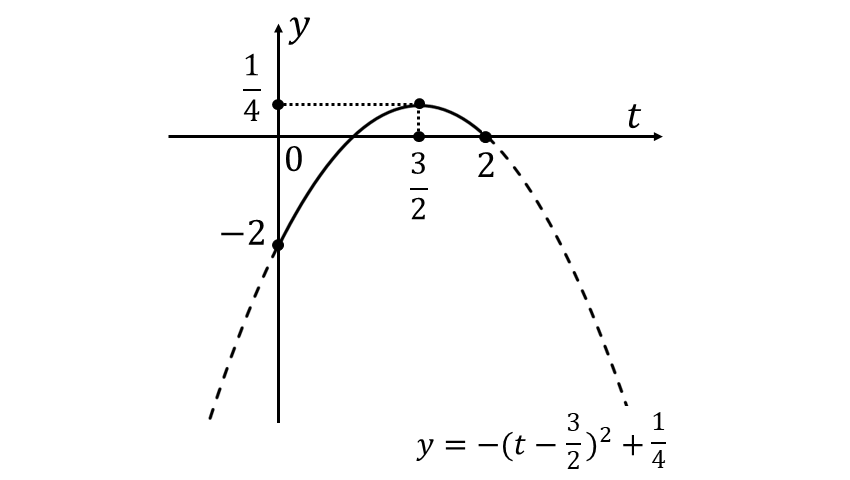
上図から\(\displaystyle\large{\hspace{3pt}t=\frac{3}{2}\hspace{2pt}}\)のとき最大値は\(\displaystyle\large{\hspace{1pt}\frac{1}{4}\hspace{2pt}}\)、\(\large{\hspace{3pt}t=0\hspace{2pt}}\)のとき最小値は\(\large{\hspace{1pt}-2\hspace{2pt}}\)となります。
ここで、\(\large{\log_3 x = t\hspace{2pt}}\)であるため、\(\displaystyle\large{t=\frac{3}{2}\hspace{2pt}}\)のときの\(\large{\hspace{1pt}x\hspace{2pt}}\)は
\begin{eqnarray}
\large
\log_3 x &\large =&\large\frac{3}{2}\\[0.7em]
\large
x &\large =&\large 3^{\frac{3}{2}}\\[0.7em]
\large
&\large =&\large 3\sqrt{3}\\[0.7em]
\\[0.7em]
\end{eqnarray}
また、\(\large{t=0\hspace{2pt}}\)のときの\(\large{\hspace{1pt}x\hspace{2pt}}\)は
\begin{eqnarray}
\large
\log_3 x &\large =&\large 0\\[0.7em]
\large
x &\large =&\large 3^0\\[0.7em]
\large
&\large =&\large 1\\[0.7em]
\\[0.7em]
\end{eqnarray}
したがって、問題の関数は
\(\large{x=3\sqrt{3}\hspace{3pt}}\)のとき最大値は\(\displaystyle\large{\hspace{2pt}\frac{1}{4}}\)
\(\large{x=1\hspace{3pt}}\)のとき最小値は\(\large{\hspace{2pt}-2}\)
と求められます。
・問題4 | 条件が多項式で与えられた場合
\(\displaystyle\large{z=(\log_2 \hspace{1pt}x)\hspace{1pt}(\log_2 \hspace{1pt}y)}\)
の最大値・最小値を求めよ
まず与えられた条件の\(\large{\hspace{1pt}x\hspace{2pt}}\)と\(\large{\hspace{1pt}y\hspace{2pt}}\)を対数に変換し、式の形を対数に統一します。
\(\large{x \geqq 2\hspace{2pt},\hspace{1pt}y \geqq 2\hspace{2pt}}\)の両辺を底が\(\large{\hspace{1pt}2\hspace{2pt}}\)の対数に変形すると $$\large{\log_2 x \geqq 1\hspace{2pt},\hspace{4pt}\log_2 y \geqq 1}$$ となります。
また、\(\large{x \geqq 2\hspace{2pt},\hspace{1pt}y \geqq 2\hspace{2pt}}\)より\(\large{\hspace{1pt}xy > 0\hspace{2pt}}\)であることから\(\large{\hspace{3pt}xy = 32\hspace{3pt}}\)の両辺に底が\(\large{\hspace{1pt}2\hspace{2pt}}\)の対数をとると
$$\large{\log_2 xy =\large \log_2 32}$$
上式を対数の公式
$$\large{\log_a MN = \log_a M + \log_a N}$$
から変形すると
$$\large{\log_2 x + \log_2 y\ = 5 }$$
となります。
ここで\(\large{\hspace{3pt}\log_2 x=X\hspace{2pt},}\)\(\large{\hspace{3pt}\log_2 y=Y\hspace{2pt}}\)とおくと、\(\large{X \geqq 1\hspace{2pt},\hspace{1pt}Y \geqq 1}\)\(\large{\hspace{1pt},\hspace{2pt}X + Y = 5\hspace{2pt}}\)となります。
条件式を\(\large{\hspace{1pt}X\hspace{2pt}}\)のみで表すと $$\large{ 5-X=Y} $$ \(\large{Y \geqq 1}\)から $$\large{5-X \geqq 1}$$ すなわち $$\large{X \leqq 4}$$ となります。
\(\large{X \geqq 1\hspace{2pt}}\)との共通範囲をとると\(\large{\hspace{1pt}X\hspace{2pt}}\)の範囲は $$\large{1 \leqq X \leqq 4}$$ となります。
ここで\(\large{\hspace{2pt}z=(\log_2 \hspace{1pt}x)\hspace{1pt}(\log_2 \hspace{1pt}y)\hspace{2pt}}\)を変形すると \begin{eqnarray} \large z &\large =&\large (\log_2 \hspace{1pt}x)\hspace{1pt}(\log_2 \hspace{1pt}y)\\[0.7em] \large &\large =&\large X\hspace{1pt}Y\\[0.7em] \large &\large =&\large X\hspace{1pt}(5-X)\\[0.7em] \large &\large =&\large -X^2 + 5X\\[0.7em] \end{eqnarray} となります。
\(\large{z=-X^2 + 5X\hspace{2pt}}\)を平方完成すると \begin{eqnarray} \large z &\large =&\large -(X^2-5X)\\[0.7em] \large &\large =&\large -\left(X-\frac{5}{2}\right)^2 +\frac{25}{4}\\[0.7em] \end{eqnarray} となります。
上式のグラフを描くと以下のようになります。
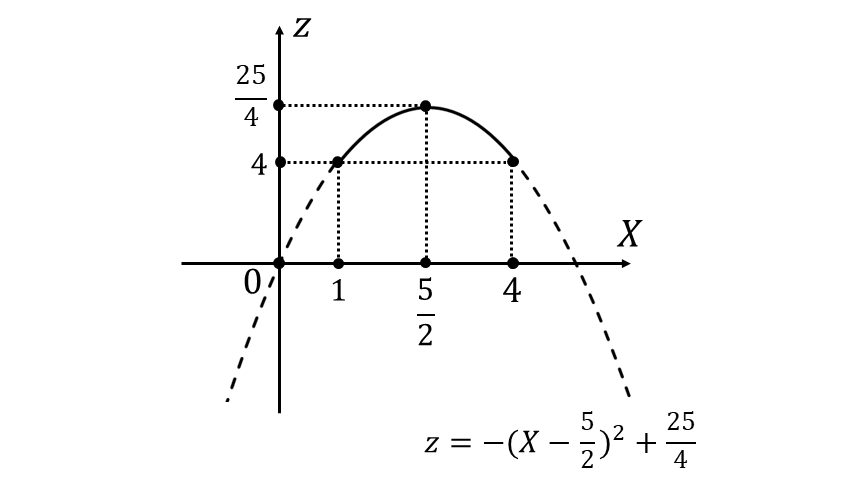
上図から\(\displaystyle\large{\hspace{3pt}X=\frac{5}{2}\hspace{3pt}}\)のとき最大値は\(\displaystyle\large{\hspace{1pt}\frac{25}{4}\hspace{2pt}}\)、\(\displaystyle\large{\hspace{3pt}X=1\hspace{1pt},\hspace{2pt}4\hspace{3pt}}\)のとき最小値は\(\large{\hspace{1pt}4\hspace{3pt}}\)となります。
ここで\(\displaystyle\large{\hspace{2pt}X=\frac{5}{2}\hspace{3pt}}\)のとき\(\displaystyle\large{\hspace{1pt}Y=\frac{5}{2}\hspace{2pt}}\)、\(\large{X=1\hspace{3pt}}\)のとき\(\large{\hspace{1pt}Y=4\hspace{2pt}}\)、\(\large{X=4\hspace{3pt}}\)のとき\(\large{\hspace{1pt}Y=1\hspace{2pt}}\)となります。
\(\large{\log_2 x = X\hspace{2pt},\hspace{2pt}\log_2 y = Y\hspace{3pt}}\)すなわち\(\large{\hspace{3pt}x = 2^X\hspace{2pt},\hspace{2pt}y = 2^Y\hspace{3pt}}\)から変形すると
\(\large{x=4\sqrt{2}\hspace{2pt},\hspace{2pt}y=4\sqrt{2}\hspace{3pt}}\)のとき最大値は\(\displaystyle\large{\hspace{2pt}\frac{25}{4}}\)
\(\large{x=2\hspace{2pt},\hspace{2pt}y=16\hspace{2pt}}\)または\(\large{\hspace{2pt}x=16\hspace{2pt},\hspace{2pt}y=2\hspace{2pt}}\)のとき最小値は\(\large{\hspace{2pt}4}\)
と求められます。