常用対数表
本項では以下の内容を解説しています。
- ・常用対数表の使い方
- ・常用対数表に関連する例題
- ・常用対数表
【1】常用対数表の使い方
常用対数とは底が\(\large{\hspace{1pt}10\hspace{2pt}}\)の対数\(\large{\hspace{1pt}\log_{10} \rm{M}\hspace{3pt}}\)のことをいいます。
例えば\(\large{\hspace{2pt}\rm{M}= 100\hspace{3pt}}\)の常用対数は $$\large{\log_{10}100 = \log_{10}10^2 = 2 }$$ また、\(\large{\rm{M}= 1000\hspace{3pt}}\)の常用対数は $$\large{\log_{10}1000 = \log_{10}10^3 = 3 }$$ となります。
・常用対数の例
よく使われる常用対数をまとめると、以下の表のようになります。
| 真数 | 常用対数の値 |
|---|---|
| \(\displaystyle \large{1}\) | \(\displaystyle \large{\log_{10} 1 = 0}\) |
| \(\displaystyle \large{2}\) | \(\displaystyle \hspace{25pt}\large{\log_{10} 2 = 0.3010}\) |
| \(\displaystyle \large{3}\) | \(\displaystyle \hspace{25pt}\large{\log_{10} 3 = 0.4771}\) |
| \(\displaystyle \large{7}\) | \(\displaystyle \hspace{25pt}\large{\log_{10} 7 = 0.8451}\) |
| \(\displaystyle \large{10}\) | \(\displaystyle \hspace{5pt}\large{\log_{10} 10 = 1}\) |
| \(\displaystyle \large{100}\) | \(\displaystyle \hspace{9pt}\large{\log_{10} 10^2 = 2}\) |
| \(\displaystyle \large{1000}\) | \(\displaystyle \hspace{9pt}\large{\log_{10} 10^3 = 3}\) |
・常用対数表とは
一般的にある正の数\(\large{\hspace{1pt}\rm{M}\hspace{2pt}}\)は $$\large{\rm{M}= \mathit{a} \times 10^\mathit{n} }$$ と表されます。(ただし\(\large{\hspace{2pt}1 \leqq a < 10\hspace{2pt}}\)、\(\large{n\hspace{2pt}}\)は整数)
ここで\(\large{\hspace{3pt}\rm{M}= \mathit{a} \times 10^\mathit{n} \hspace{3pt}}\)に常用対数をとると \begin{eqnarray} \large \log_{10} \rm{M} &\large =&\large \log_{10} (\mathit{a} \times 10^\mathit{n})\\[0.7em] \large &\large =&\large \log_{10} \mathit{a} + \log_{10}10^\mathit{n} \\[0.7em] \large &\large =&\large \color{red}{\log_{10} a}\color{black}{} + \color{blue}{n} \\[0.7em] \end{eqnarray} となります。
このとき\(\large{\hspace{3pt}1 \leqq a < 10\hspace{2pt}}\)であることから、\(\large{0 \leqq \log_{10}a < 1\hspace{2pt}}\)となります。
また、\(\large{n\hspace{2pt}}\)は値\(\large{\hspace{1pt}\rm{M}\hspace{2pt}}\)の桁数に対応する整数となります。
すなわち、任意の正の数\(\large{\hspace{1pt}\rm{M}\hspace{2pt}}\)の常用対数\(\large{\hspace{1pt}\log_{10}\rm{M}\hspace{2pt}}\)を求めたい場合は $$\large{\log_{10} \rm{M} = \color{red}{\log_{10} \mathit{a}}\color{black}{} + \color{blue}{n}}$$ の形に変形することで、真数が\(\large{\hspace{1pt}1\hspace{2pt}}\)以上\(\large{\hspace{1pt}10\hspace{2pt}}\)未満の常用対数\(\large{\hspace{1pt}\color{red}{\log_{10} \mathit{a}}\hspace{2pt}}\)と整数\(\large{\hspace{1pt}n\hspace{2pt}}\)の値から求めることができます。
真数が\(\large{\hspace{1pt}1\hspace{2pt}}\)以上\(\large{\hspace{1pt}10\hspace{2pt}}\)未満の常用対数の値をまとめた表を常用対数表といいます。
常用対数表は本項の後半に記載しています。
・常用対数表の使い方
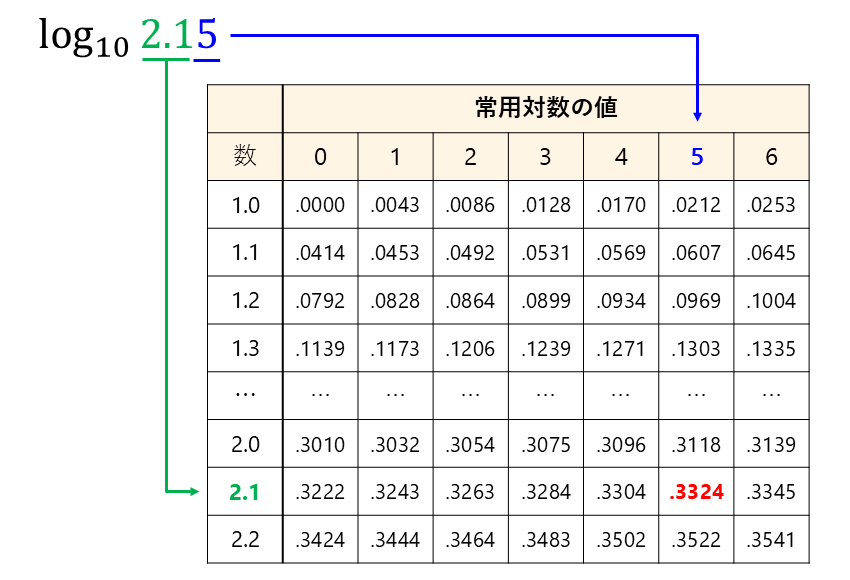
常用対数表の使い方は、縦方向に『真数の上から二桁』、横方向に『真数の小数点第二位』の値を探し、その行と列が重なる位置の値を読みます。
例えば、\(\large{\hspace{1pt}\log_{10}2.15\hspace{2pt}}\)の場合は縦方向に『真数の上から二桁の\(\large{\hspace{1pt}2.1\hspace{2pt}}\)』、横方向に『真数の小数点第二位の\(\large{\hspace{1pt}5\hspace{2pt}}\)』を見つけて行と列が重なる位置の値を読みます。
以下の常用対数表から\(\large{\hspace{2pt}.3324\hspace{2pt}}\)とあるため常用対数\(\large{\hspace{1pt}\log_{10}2.15\hspace{2pt}}\)の値は
$$\large{\large{\hspace{1pt}\log_{10}2.15\hspace{2pt}=0.3324}}$$
となります。
・例題1
\(\large{\hspace{5pt}\log_{10}1.55}\)
常用対数表から縦方向に『真数の上二桁の\(\large{\hspace{1pt}1.5\hspace{2pt}}\)』、横方向に『真数の小数点第二位の\(\large{\hspace{1pt}5\hspace{2pt}}\)』を見つけ、その行と列が重なる値を読むと\(\large{\hspace{1pt}.1903\hspace{2pt}}\)となります。
したがって $$\large{\log_{10}1.55 = 0.1903}$$ と求められます。
・例題2
\(\large{\hspace{5pt}\log_{10}31400\hspace{8pt}}\)
\(\large{\hspace{1pt}\log_{10}31400\hspace{2pt}}\)を変形すると \begin{eqnarray} \large \log_{10} 31400 &\large =&\large \log_{10} (3.14 \times 10^4)\\[0.7em] \large &\large =&\large \log_{10} 3.14 + \log_{10}10^4 \\[0.7em] \large &\large =&\large \log_{10} 3.14 + 4 \\[0.7em] \end{eqnarray} ここで、常用対数表から\(\large{\hspace{1pt}\log_{10} 3.14\hspace{2pt}}\)の値を求めると縦方向に『真数の上二桁の\(\large{\hspace{1pt}3.1\hspace{2pt}}\)』、横方向に『真数の小数点第二位の\(\large{\hspace{1pt}4\hspace{2pt}}\)』を見つけ、その行と列が重なる値を読むと\(\large{\hspace{1pt}.4969\hspace{2pt}}\)となるため $$\large{\log_{10}3.14 = 0.4969}$$ と求められます。
したがって、 \begin{eqnarray} \large \log_{10} 31400 &\large =&\large \log_{10} 3.14 + 4\\[0.7em] \large &\large =&\large 0.4969 + 4\\[0.7em] \large &\large =&\large 4.4969 \\[0.7em] \end{eqnarray} と求められます。
・例題3
\(\large{\hspace{5pt}\log_{10}0.00119}\)
\(\large{\hspace{1pt}\log_{10}0.00119\hspace{2pt}}\)を変形すると \begin{eqnarray} \large \log_{10} 0.00119 &\large =&\large \log_{10} (1.19 \times 10^{-3})\\[0.7em] \large &\large =&\large \log_{10} 1.19 + \log_{10}10^{-3} \\[0.7em] \large &\large =&\large \log_{10} 1.19 -3 \\[0.7em] \end{eqnarray} ここで、常用対数表から\(\large{\hspace{1pt}\log_{10} 1.19\hspace{2pt}}\)の値を求めると縦方向に『真数の上二桁の\(\large{\hspace{1pt}1.1\hspace{2pt}}\)』、横方向に『真数の小数点第二位の\(\large{\hspace{1pt}9\hspace{2pt}}\)』を見つけ、その行と列が重なる値を読むと\(\large{\hspace{1pt}.0755\hspace{2pt}}\)となるため $$\large{\log_{10}1.19 = 0.0755}$$ と求められます。
したがって、 \begin{eqnarray} \large \log_{10} 0.00119 &\large =&\large \log_{10} 1.19 -3\\[0.7em] \large &\large =&\large 0.0755 -3\\[0.7em] \large &\large =&\large -2.9245 \\[0.7em] \end{eqnarray} と求められます。
【2】常用対数表
本章では、常用対数表を示します。
・常用対数表①
| 常用対数の値 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1.0 | .0000 | .0043 | .0086 | .0128 | .0170 | .0212 | .0253 | .0294 | .0334 | .0374 |
| 1.1 | .0414 | .0453 | .0492 | .0531 | .0569 | .0607 | .0645 | .0682 | .0719 | .0755 |
| 1.2 | .0792 | .0828 | .0864 | .0899 | .0934 | .0969 | .1004 | .1038 | .1072 | .1106 |
| 1.3 | .1139 | .1173 | .1206 | .1239 | .1271 | .1303 | .1335 | .1367 | .1399 | .1430 |
| 1.4 | .1461 | .1492 | .1523 | .1553 | .1584 | .1614 | .1644 | .1673 | .1703 | .1732 |
| 1.5 | .1761 | .1790 | .1818 | .1847 | .1875 | .1903 | .1931 | .1959 | .1987 | .2014 |
| 1.6 | .2041 | .2068 | .2095 | .2122 | .2148 | .2175 | .2201 | .2227 | .2253 | .2279 |
| 1.7 | .2304 | .2330 | .2355 | .2380 | .2405 | .2430 | .2455 | .2480 | .2504 | .2529 |
| 1.8 | .2553 | .2577 | .2601 | .2625 | .2648 | .2672 | .2695 | .2718 | .2742 | .2765 |
| 1.9 | .2788 | .2810 | .2833 | .2856 | .2878 | .2900 | .2923 | .2945 | .2967 | .2989 |
| 2.0 | .3010 | .3032 | .3054 | .3075 | .3096 | .3118 | .3139 | .3160 | .3181 | .3201 |
| 2.1 | .3222 | .3243 | .3263 | .3284 | .3304 | .3324 | .3345 | .3365 | .3385 | .3404 |
| 2.2 | .3424 | .3444 | .3464 | .3483 | .3502 | .3522 | .3541 | .3560 | .3579 | .3598 |
| 2.3 | .3617 | .3636 | .3655 | .3674 | .3692 | .3711 | .3729 | .3747 | .3766 | .3784 |
| 2.4 | .3802 | .3820 | .3838 | .3856 | .3874 | .3892 | .3909 | .3927 | .3945 | .3962 |
| 2.5 | .3979 | .3997 | .4014 | .4031 | .4048 | .4065 | .4082 | .4099 | .4116 | .4133 |
| 2.6 | .4150 | .4166 | .4183 | .4200 | .4216 | .4232 | .4249 | .4265 | .4281 | .4298 |
| 2.7 | .4314 | .4330 | .4346 | .4362 | .4378 | .4393 | .4409 | .4425 | .4440 | .4456 |
| 2.8 | .4472 | .4487 | .4502 | .4518 | .4533 | .4548 | .4564 | .4579 | .4594 | .4609 |
| 2.9 | .4624 | .4639 | .4654 | .4669 | .4683 | .4698 | .4713 | .4728 | .4742 | .4757 |
| 3.0 | .4771 | .4786 | .4800 | .4814 | .4829 | .4843 | .4857 | .4871 | .4886 | .4900 |
| 3.1 | .4914 | .4928 | .4942 | .4955 | .4969 | .4983 | .4997 | .5011 | .5024 | .5038 |
| 3.2 | .5051 | .5065 | .5079 | .5092 | .5105 | .5119 | .5132 | .5145 | .5159 | .5172 |
| 3.3 | .5185 | .5198 | .5211 | .5224 | .5237 | .5250 | .5263 | .5276 | .5289 | .5302 |
| 3.4 | .5315 | .5328 | .5340 | .5353 | .5366 | .5378 | .5391 | .5403 | .5416 | .5428 |
| 3.5 | .5441 | .5453 | .5465 | .5478 | .5490 | .5502 | .5514 | .5527 | .5539 | .5551 |
| 3.6 | .5563 | .5575 | .5587 | .5599 | .5611 | .5623 | .5635 | .5647 | .5658 | .5670 |
| 3.7 | .5682 | .5694 | .5705 | .5717 | .5729 | .5740 | .5752 | .5763 | .5775 | .5786 |
| 3.8 | .5798 | .5809 | .5821 | .5832 | .5843 | .5855 | .5866 | .5877 | .5888 | .5899 |
| 3.9 | .5911 | .5922 | .5933 | .5944 | .5955 | .5966 | .5977 | .5988 | .5999 | .6010 |
| 4.0 | .6021 | .6031 | .6042 | .6053 | .6064 | .6075 | .6085 | .6096 | .6107 | .6117 |
| 4.1 | .6128 | .6138 | .6149 | .6160 | .6170 | .6180 | .6191 | .6201 | .6212 | .6222 |
| 4.2 | .6232 | .6243 | .6253 | .6263 | .6274 | .6284 | .6294 | .6304 | .6314 | .6325 |
| 4.3 | .6335 | .6345 | .6355 | .6365 | .6375 | .6385 | .6395 | .6405 | .6415 | .6425 |
| 4.4 | .6435 | .6444 | .6454 | .6464 | .6474 | .6484 | .6493 | .6503 | .6513 | .6522 |
| 4.5 | .6532 | .6542 | .6551 | .6561 | .6571 | .6580 | .6590 | .6599 | .6609 | .6618 |
| 4.6 | .6628 | .6637 | .6646 | .6656 | .6665 | .6675 | .6684 | .6693 | .6702 | .6712 |
| 4.7 | .6721 | .6730 | .6739 | .6749 | .6758 | .6767 | .6776 | .6785 | .6794 | .6803 |
| 4.8 | .6812 | .6821 | .6830 | .6839 | .6848 | .6857 | .6866 | .6875 | .6884 | .6893 |
| 4.9 | .6902 | .6911 | .6920 | .6928 | .6937 | .6946 | .6955 | .6964 | .6972 | .6981 |
| 5.0 | .6990 | .6998 | .7007 | .7016 | .7024 | .7033 | .7042 | .7050 | .7059 | .7067 |
| 5.1 | .7076 | .7084 | .7093 | .7101 | .7110 | .7118 | .7126 | .7135 | .7143 | .7152 |
| 5.2 | .7160 | .7168 | .7177 | .7185 | .7193 | .7202 | .7210 | .7218 | .7226 | .7235 |
| 5.3 | .7243 | .7251 | .7259 | .7267 | .7275 | .7284 | .7292 | .7300 | .7308 | .7316 |
| 5.4 | .7324 | .7332 | .7340 | .7348 | .7356 | .7364 | .7372 | .7380 | .7388 | .7396 |
・常用対数表②
| 常用対数の値 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 5.5 | .7404 | .7412 | .7419 | .7427 | .7435 | .7443 | .7451 | .7459 | .7466 | .7474 |
| 5.6 | .7482 | .7490 | .7497 | .7505 | .7513 | .7520 | .7528 | .7536 | .7543 | .7551 |
| 5.7 | .7559 | .7566 | .7574 | .7582 | .7589 | .7597 | .7604 | .7612 | .7619 | .7627 |
| 5.8 | .7634 | .7642 | .7649 | .7657 | .7664 | .7672 | .7679 | .7686 | .7694 | .7701 |
| 5.9 | .7709 | .7716 | .7723 | .7731 | .7738 | .7745 | .7752 | .7760 | .7767 | .7774 |
| 6.0 | .7782 | .7789 | .7796 | .7803 | .7810 | .7818 | .7825 | .7832 | .7839 | .7846 |
| 6.1 | .7853 | .7860 | .7868 | .7875 | .7882 | .7889 | .7896 | .7903 | .7910 | .7917 |
| 6.2 | .7924 | .7931 | .7938 | .7945 | .7952 | .7959 | .7966 | .7973 | .7980 | .7987 |
| 6.3 | .7993 | .8000 | .8007 | .8014 | .8021 | .8028 | .8035 | .8041 | .8048 | .8055 |
| 6.4 | .8062 | .8069 | .8075 | .8082 | .8089 | .8096 | .8102 | .8109 | .8116 | .8122 |
| 6.5 | .8129 | .8136 | .8142 | .8149 | .8156 | .8162 | .8169 | .8176 | .8182 | .8189 |
| 6.6 | .8195 | .8202 | .8209 | .8215 | .8222 | .8228 | .8235 | .8241 | .8248 | .8254 |
| 6.7 | .8261 | .8267 | .8274 | .8280 | .8287 | .8293 | .8299 | .8306 | .8312 | .8319 |
| 6.8 | .8325 | .8331 | .8338 | .8344 | .8351 | .8357 | .8363 | .8370 | .8376 | .8382 |
| 6.9 | .8388 | .8395 | .8401 | .8407 | .8414 | .8420 | .8426 | .8432 | .8439 | .8445 |
| 7.0 | .8451 | .8457 | .8463 | .8470 | .8476 | .8482 | .8488 | .8494 | .8500 | .8506 |
| 7.1 | .8513 | .8519 | .8525 | .8531 | .8537 | .8543 | .8549 | .8555 | .8561 | .8567 |
| 7.2 | .8573 | .8579 | .8585 | .8591 | .8597 | .8603 | .8609 | .8615 | .8621 | .8627 |
| 7.3 | .8633 | .8639 | .8645 | .8651 | .8657 | .8663 | .8669 | .8675 | .8681 | .8686 |
| 7.4 | .8692 | .8698 | .8704 | .8710 | .8716 | .8722 | .8727 | .8733 | .8739 | .8745 |
| 7.5 | .8751 | .8756 | .8762 | .8768 | .8774 | .8779 | .8785 | .8791 | .8797 | .8802 |
| 7.6 | .8808 | .8814 | .8820 | .8825 | .8831 | .8837 | .8842 | .8848 | .8854 | .8859 |
| 7.7 | .8865 | .8871 | .8876 | .8882 | .8887 | .8893 | .8899 | .8904 | .8910 | .8915 |
| 7.8 | .8921 | .8927 | .8932 | .8938 | .8943 | .8949 | .8954 | .8960 | .8965 | .8971 |
| 7.9 | .8976 | .8982 | .8987 | .8993 | .8998 | .9004 | .9009 | .9015 | .9020 | .9025 |
| 8.0 | .9031 | .9036 | .9042 | .9047 | .9053 | .9058 | .9063 | .9069 | .9074 | .9079 |
| 8.1 | .9085 | .9090 | .9096 | .9101 | .9106 | .9112 | .9117 | .9122 | .9128 | .9133 |
| 8.2 | .9138 | .9143 | .9149 | .9154 | .9159 | .9165 | .9170 | .9175 | .9180 | .9186 |
| 8.3 | .9191 | .9196 | .9201 | .9206 | .9212 | .9217 | .9222 | .9227 | .9232 | .9238 |
| 8.4 | .9243 | .9248 | .9253 | .9258 | .9263 | .9269 | .9274 | .9279 | .9284 | .9289 |
| 8.5 | .9294 | .9299 | .9304 | .9309 | .9315 | .9320 | .9325 | .9330 | .9335 | .9340 |
| 8.6 | .9345 | .9350 | .9355 | .9360 | .9365 | .9370 | .9375 | .9380 | .9385 | .9390 |
| 8.7 | .9395 | .9400 | .9405 | .9410 | .9415 | .9420 | .9425 | .9430 | .9435 | .9440 |
| 8.8 | .9445 | .9450 | .9455 | .9460 | .9465 | .9469 | .9474 | .9479 | .9484 | .9489 |
| 8.9 | .9494 | .9499 | .9504 | .9509 | .9513 | .9518 | .9523 | .9528 | .9533 | .9538 |
| 9.0 | .9542 | .9547 | .9552 | .9557 | .9562 | .9566 | .9571 | .9576 | .9581 | .9586 |
| 9.1 | .9590 | .9595 | .9600 | .9605 | .9609 | .9614 | .9619 | .9624 | .9628 | .9633 |
| 9.2 | .9638 | .9643 | .9647 | .9652 | .9657 | .9661 | .9666 | .9671 | .9675 | .9680 |
| 9.3 | .9685 | .9689 | .9694 | .9699 | .9703 | .9708 | .9713 | .9717 | .9722 | .9727 |
| 9.4 | .9731 | .9736 | .9741 | .9745 | .9750 | .9754 | .9759 | .9763 | .9768 | .9773 |
| 9.5 | .9777 | .9782 | .9786 | .9791 | .9795 | .9800 | .9805 | .9809 | .9814 | .9818 |
| 9.6 | .9823 | .9827 | .9832 | .9836 | .9841 | .9845 | .9850 | .9854 | .9859 | .9863 |
| 9.7 | .9868 | .9872 | .9877 | .9881 | .9886 | .9890 | .9894 | .9899 | .9903 | .9908 |
| 9.8 | .9912 | .9917 | .9921 | .9926 | .9930 | .9934 | .9939 | .9943 | .9948 | .9952 |
| 9.9 | .9956 | .9961 | .9965 | .9969 | .9974 | .9978 | .9983 | .9987 | .9991 | .9996 |