対数の大小比較

本項では、『対数の大小比較の問題』 について解説します。

【1】対数の大小比較

対数関数 \(\large{y=\log_a x}\) は、対数のグラフの特徴から、底が \(\large{1}\) より大きい場合は 単調増加 (\(\large{x}\)が増加すると、\(\large{y}\)も常に増加) の性質があります。

したがって、\(\large{a > 1}\) のときは、下図のように 真数\(\large{\hspace{3pt}M,N\hspace{3pt}}\)の大小関係が 対数\(\large{\hspace{3pt}\log_a M,\hspace{1pt}\log_a N\hspace{3pt}}\)の大小関係と一致します。

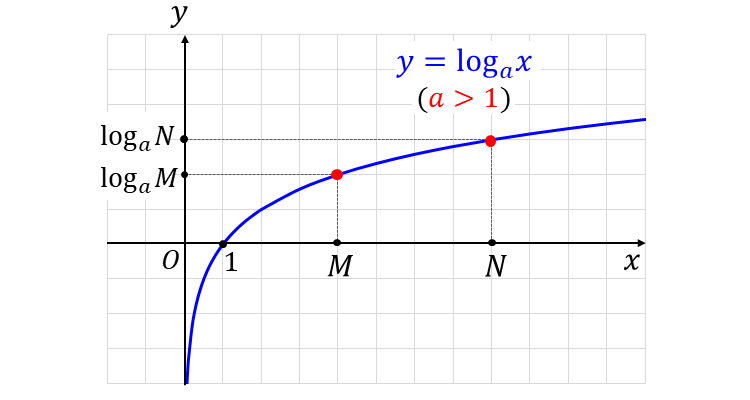
一方、底が \(\large{1}\) より小さい対数関数は 単調減少 (\(\large{x}\)が増加すると、\(\large{y}\)は常に減少) の性質があります。

\(\large{0 < a < 1}\) のときは、下図のように 真数\(\large{\hspace{3pt}M,N\hspace{3pt}}\)の大小関係 と 対数\(\large{\hspace{3pt}\log_a M,\hspace{1pt}\hspace{3pt}\log_a N\hspace{3pt}}\)の大小関係は反転します。

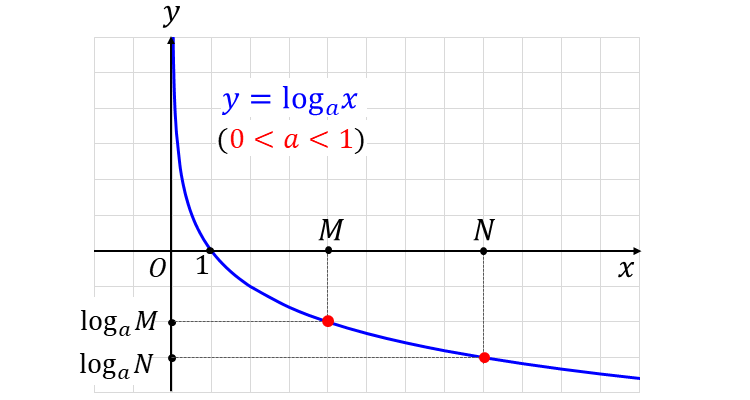
以上の対数の大小関係をまとめると、以下のようになります

本章では、対数の大小関係に関連した問題について解説します。

【1-1】底をそろえる問題(底aが1より大きい場合)

まず、以下のような問題について考えます。

対数の大小比較をするときは、『底をそろえて真数を比較』することが基本です。

問題の \(\large{\log_4 9}\) の底を \(\large{2}\) に変換することで大小関係を求めます。
底の変換公式 \(\displaystyle \large {\log_a b = \frac{\log_c b}{\log_c a}}\) から \begin{eqnarray} \large \log_4 9&\large =&\large \frac{\log_2 9 }{\log_2 4 } \\[0.7em] \large &\large =&\large \frac{\log_2 3^2 }{\log_2 2^2 } \\[0.7em] \large &\large =&\large \frac{2 \log_2 3 }{2} \\[0.7em] \large &\large =&\large \log_2 3 \\[0.7em] \end{eqnarray}

ここで、底\(\large{2}\) は \(\large{1}\) より大きく、真数の大小関係が 対数の大小関係と一致するため、以下が成り立ちます。 $$\large{\log_2 6 > \log_2 3}$$ したがって、 $$\large{\log_2 6 > \log_4 9}$$ となります。

\(\large{y=\log_2 x}\) に \(\large{x=3}\) と \(\large{x=6}\) の点をプロットした図を示します。

対数の大小関係の問題を解くときは、上図のような対数関数のグラフを描くことで 大小関係が分かりやすくなります。

【1-2】底をそろえる問題(底aが1より小さい場合)

次に、以下のような問題について考えます。

前問と同じように、対数の大小比較の問題は『底をそろえて真数を比較』することが基本です。

問題の \(\large{\log_\frac{1}{4} 9}\) の底を \(\large{\frac{1}{2}}\) に変換することで大小関係を求めます。
底の変換公式 \(\displaystyle \large {\log_a b = \frac{\log_c b}{\log_c a}}\) から \begin{eqnarray} \large \log_\frac{1}{4} 9&\large =&\large \frac{\log_\frac{1}{2} 9 }{\log_\frac{1}{2} \frac{1}{4} } \\[0.7em] \large &\large =&\large \frac{\log_\frac{1}{2} 3^2 }{\log_\frac{1}{2} \left(\frac{1}{2}\right)^2 } \\[0.7em] \large &\large =&\large \frac{2 \log_\frac{1}{2} 3 }{2} \\[0.7em] \large &\large =&\large \log_\frac{1}{2} 3 \\[0.7em] \end{eqnarray}

ここで、底\(\large{\frac{1}{2}}\) は \(\large{1}\) より小さく、真数の大小関係が 対数の大小関係と反転するため、以下が成り立ちます。 $$\large{\log_\frac{1}{2} 3 > \log_\frac{1}{2} 5}$$ したがって、 $$\large{\log_\frac{1}{4} 9 > \log_\frac{1}{2} 5}$$ となります。

\(\large{y=\log_\frac{1}{2} x}\) に \(\large{x=3}\) と \(\large{x=5}\) の点をプロットした図を示します。

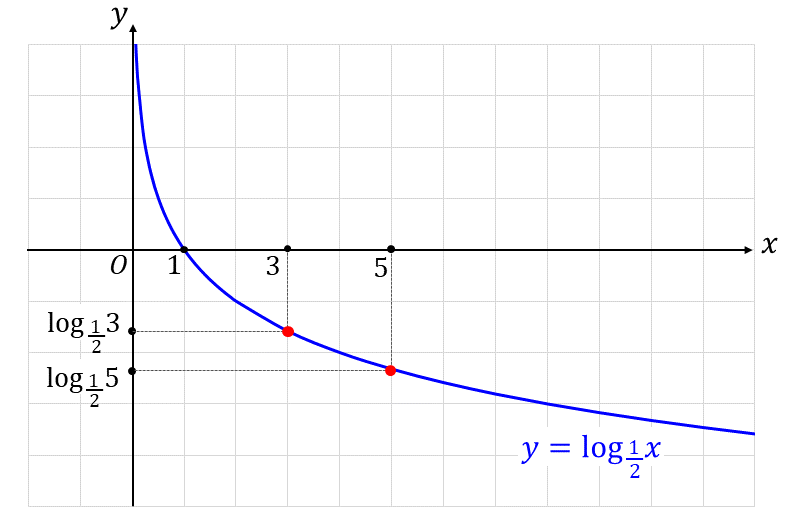
対数の大小関係の問題は、底の大きさによって大小関係が変わってしまいますが、図のような対数関数のグラフを描くことで 大小関係が分かりやすくなります。

【1-3】整数と対数の大小比較

次に、以下のような問題について考えます。

前問のように、対数どうしであれば、底をそろえることで大小の比較ができます。
そのため、整数を対数に置き換えることで 大小を比較できるようにします。

整数の \(\large{3}\) を底が \(\large{2}\) の対数に変形すると、以下のようになります。 \begin{eqnarray} \large 3&\large =&\large 3 \times \log_2 2 \\[0.7em] \large &\large =&\large \log_2 2^3 \\[0.7em] \large &\large =&\large \log_2 8 \\[0.7em] \end{eqnarray}

ここで、底\(\large{2}\) は \(\large{1}\) より大きく、真数の大小関係が 対数の大小関係と一致するため、以下が成り立ちます。 $$\large{\log_2 8 < \log_2 9}$$ したがって、 $$\large{3 < \log_2 9}$$ となります。

【2】対数の大小比較の応用問題

本章では、対数の大小比較の応用問題について解説します。

【2-1】整数と対数の比較

与えられた2つの対数は、底の変換公式から底をそろえても、ただちに大小を比較することができません。

この問題では、それぞれの対数を整数と比較することで大小関係を求めます。

\(\large{\log_2 6}\) は底が1より大きいため、以下の大小関係が成り立ちます。 $$\large{\log_2 4 < \log_2 6 < \log_2 8}$$ $$\large{\log_2 2^2 < \log_2 6 < \log_2 2^3}$$ したがって、\(\large{\log_2 6}\) は以下の不等式を満たします。 $$\large{2 < \log_2 6 < 3}$$

また、\(\large{\log_3 7}\) は底が1より大きいため、以下の大小関係が成り立ちます。 $$\large{\log_3 3 < \log_3 7 < \log_3 9}$$ $$\large{\log_3 3^1 < \log_3 7 < \log_3 3^2}$$ したがって、\(\large{\log_3 7}\) は以下の不等式を満たします。 $$\large{1 < \log_3 7 < 2}$$

以上から、『 \(\large{2 < \log_2 6 < 3}\) 』と『 \(\large{1 < \log_3 7 < 2}\) 』 の関係から、以下の大小関係が求められます。 $$\large{\log_3 7 < \log_2 6}$$

【2-2】文字式の対数の大小比較

文字式を含んだ対数の大小関係を求める問題です。

対数の真数が 文字式の積や分数を含んでいるため、対数の公式 $$\large{\log_a{MN} = \log_a M+ \log_a N}$$ $$\large{\log_a \frac{M}{N} = \log_a M - \log_a N}$$ を利用して、一種類のみの文字になるように分解します。

また、底が異なるため、底の変換公式 $$\large{\displaystyle \large{\log_x y= \frac{1}{\log_y x}}}$$ を利用して、底をそろえます。

\(\displaystyle \large{\log_a ab}\) を変形すると \begin{eqnarray} \large \log_a {ab}&\large =&\large \log_a a + \log_a b \\ \large &\large =&\large \color{red}{1+ \log_a b} \\ \end{eqnarray}

また、\(\displaystyle \large{\log_b \frac{b}{a}}\) を変形すると、 \begin{eqnarray} \large \log_b \frac{b}{a}&\large =&\large \log_b b - \log_b a \\ \large &\large =&\large 1-\log_b a \\ \large &\large =&\large \color{blue}{1-\frac{1}{\log_a b}} \\ \end{eqnarray}

ここで、与えらた条件 \(\large{1 < a < b }\) から、 $$\large{ \log_a b > 1}$$ が成り立ちます。
(\(\large{a,b}\) に対して底\(\large{a}\)の対数をとると、\(\large{\log_a a < \log_a b}\) すなわち、\(\large{1 < \log_a b}\) となるため。)

よって、 $$\large{\color{blue}{1-\frac{1}{\log_a b}}\color{black}{} < \color{red}{1+ \log_a b}}$$ が成り立つため、求める大小関係は $$\large{\log_b \frac{b}{a} < \log_a ab}$$ となります。

---