サラスの公式
【1】サラスの公式
サラスの公式 (もしくは、サラスの方法) とは『三次正方行列の行列式の計算を示す規則』であり、行列式の計算を暗記する方法として知られています。
三次正方行列の行列式は 物理・工学の分野で頻繁に計算しますが、式が複雑なため、そのまま暗記することは難しいです。
サラスの公式では、行列式の計算を 規則に当てはめることで 簡単に覚えることができます。
・3×3行列の行列式
三次正方行列の行列式は、以下のように定義されます。
サラスの公式では、上記の行列式を以下のような規則で計算します。
・左上から右下への積(①~③)は 正の符号
右上から左下への積(④~⑥)は 負の符号
で足し合わせる
以下にサラスの公式による規則を 図に表したものを示します。
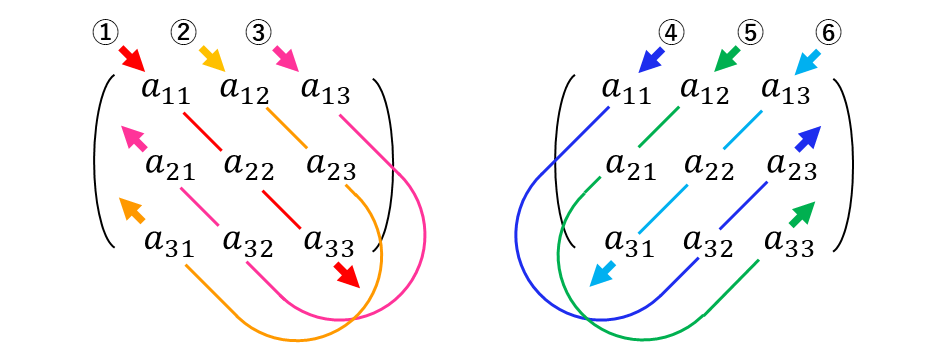
サラスの公式による規則から、以下のように行列式を計算します。 \begin{eqnarray} \large |A|&\large =&\large \mathbf{① + ②+③}\\[0.7em] \large &\large &\large \mathbf{-④-⑤-⑥}\\[1em] \large &\large =&\large a_{11}\hspace{1pt}a_{22}\hspace{1pt}a_{33} + a_{12}\hspace{1pt}a_{23}\hspace{1pt}a_{31}+a_{13}\hspace{1pt}a_{21}\hspace{1pt}a_{32}\\[0.7em] \large &\large &\large -a_{11}\hspace{1pt}a_{23}\hspace{1pt}a_{32}-a_{12}\hspace{1pt}a_{21}\hspace{1pt}a_{33} -a_{13}\hspace{1pt}a_{22}\hspace{1pt}a_{31}\\ \end{eqnarray}
・例題
サラスの公式を利用して行列式を求めてみます。
まず、行列\(\large{A}\) の左上から右下への斜めの\(\large{\hspace{1pt}3\hspace{2pt}}\)つの成分の積を 正の符号 のままで和を計算すると、 $$\large{1 \cdot 4 \cdot 1 + 2\cdot 0\cdot 0 + 1 \cdot2 \cdot 3 = 10}$$
また、行列\(\large{A}\) の右上から左下への斜めの\(\large{\hspace{1pt}3\hspace{2pt}}\)つの成分の積を 負の符号 をつけて和を計算すると、 $$\large{-1 \cdot 2 \cdot 0 - 2\cdot 3 \cdot 1 - 1 \cdot 4 \cdot 0 = -6}$$
したがって、行列式\(\large{|A|}\) は $$\large{|A|=10-6 = 4}$$ と求めることができます。
【2】2×2行列の行列式
サラスの公式は、同じような計算の規則を 二次正方行列にも用いることができます。
三次正方行列の場合と同様に、左上から右下の斜めの成分の積を正の符号、右上から左下の斜めの成分の積を負の符号で和を計算します。
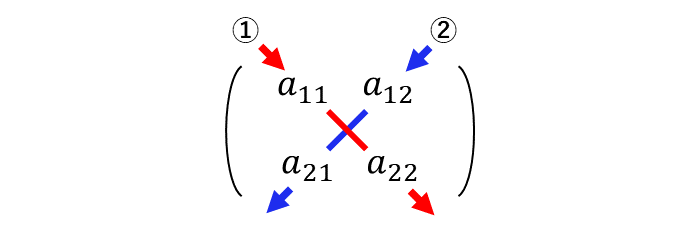
なお、サラスの公式が適用できるのは、二次正方行列 と 三次正方行列 の行列式のみです。
四次以上の行列式には適用できない点に注意が必要です。
・例題
行列\(\large{A}\) の左上から右下への斜めの成分の積は \(\large{2\times4 }\)、右上から左下への斜めの成分の積は \(\large{3\times1 }\) となります。
したがって、サラスの公式から 行列式\(\large{|A|}\) は $$\large{|A|=2\times4 -3\times1 = 5}$$ と求められます。
【3】問題と解き方
\(\large{A = \left(\begin{array}{ccc} 6 & \sqrt{2} \\ 2\sqrt{2} & 3 \\ \end{array} \right) }\)
【解答と解説】: 問題(1)
\(\large{A = \left(\begin{array}{cc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \\ \end{array} \right) }\)
【解答と解説】: 問題(2)
\(\large{A = \left(\begin{array}{ccc} 1 & 4 & 2\\ -1 & 0 & 2\\ 3 & 1 & 0\\ \end{array} \right) }\)
【解答と解説】: 問題(3)
\(\large{A = \left(\begin{array}{ccc} \cos \theta & -\sin \theta & 0\\ \sin \theta & \cos \theta & 0\\ 0 & 0 & 1\\ \end{array} \right) }\)
【解答と解説】: 問題(4)
問題(1) 2×2行列の行列式
\(\large{A = \left(\begin{array}{ccc} 6 & \sqrt{2} \\ 2\sqrt{2} & 3 \\ \end{array} \right) }\)
【解答と解説】
行列\(\large{A}\) の左上から右下への斜め方向の成分の積は \(\large{6\times3 }\)、右上から左下への斜め方向の成分の積は \(\large{\sqrt{2}\times 2\sqrt{2} }\) となります。
したがって、サラスの公式から 行列式\(\large{|A|}\) は $$\large{|A|=6\times3 -\sqrt{2}\times2\sqrt{2} = 14}$$ と求められます。
問題(2) 2×2行列 (回転行列) の行列式
\(\large{A = \left(\begin{array}{ccc} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \\ \end{array} \right) }\)
【解答と解説】
行列\(\large{A}\) の左上から右下への斜め方向の成分の積は \(\large{\cos \theta \times \cos \theta }\)、右上から左下への斜め方向の成分の積は \(\large{-\sin \theta\times \sin \theta }\) となります。
したがって、サラスの公式から 行列式\(\large{|A|}\) は $$\large{|A|=\cos \theta \times \cos \theta -(-\sin \theta\times \sin \theta) = 1}$$ と求められます。
本問の行列\(\large{A}\) は、原点を中心に\(\large{\theta\hspace{1pt}}\)だけ回転移動する\(\large{1\hspace{1pt}}\)次変換を表す行列です。
回転行列の行列式は \(\large{1}\) となります。
問題(3) 3×3行列 の行列式
\(\large{A = \left(\begin{array}{ccc} 1 & 4 & 2\\ -1 & 0 & 2\\ 3 & 1 & 0\\ \end{array} \right) }\)
【解答と解説】
まず、行列\(\large{A}\) の左上から右下への斜めの\(\large{\hspace{1pt}3\hspace{1pt}}\)つの成分の積を 正の符号 のまま和を計算すると、 $$\large{1 \cdot 0 \cdot 0 + 4\cdot 2\cdot 3 + 2 \cdot1 \cdot (-1) = 22}$$
また、行列\(\large{A}\) の右上から左下への斜めの\(\large{\hspace{1pt}3\hspace{1pt}}\)つの成分の積を 負の符号 をつけて和を計算すると、 $$\large{-1 \cdot 1 \cdot 2 - 4\cdot (-1) \cdot 0 -2 \cdot 0 \cdot 3 = -2}$$
したがって、行列式\(\large{|A|}\) は $$\large{|A|=22-2 = 20}$$ と求めることができます。
問題(4) 3×3行列 (回転行列) の行列式
\(\large{A = \left(\begin{array}{ccc} \cos \theta & -\sin \theta & 0\\ \sin \theta & \cos \theta & 0\\ 0 & 0 & 1\\ \end{array} \right) }\)
【解答と解説】
まず、行列\(\large{A}\) の左上から右下への斜めの\(\large{\hspace{1pt}3\hspace{1pt}}\)つの成分の積を 正の符号 のまま和を計算すると、 $$\large{\cos^2 \theta -0 + 0 = \cos^2 \theta}$$
また、行列\(\large{A}\) の右上から左下への斜め方向の\(\large{\hspace{1pt}3\hspace{1pt}}\)つの成分の積を 負の符号 をつけて和を計算すると、 $$\large{ -0 +\sin^2 \theta - 0 = \sin^2 \theta}$$
したがって、行列式\(\large{|A|}\) は $$\large{|A|=\cos^2 \theta + \sin^2 \theta = 1}$$ と求めることができます。
本問の行列\(\large{A}\) は、\(\large{z\hspace{1pt}}\)軸回りに\(\large{\theta\hspace{1pt}}\)だけ回転移動する\(\large{1\hspace{1pt}}\)次変換を表す行列です。
回転行列の行列式は \(\large{1}\) となります。