行列の積
【1】行列の積の定義
\(\large{2\hspace{1pt}}\)つの行列\(\large{A\hspace{1pt},B\hspace{3pt}}\)の積は以下のように定義されます。
行列の積 \(\large{C = AB}\) は、\(\large{i\hspace{1pt}}\)行\(j\hspace{1pt}\)列 の成分を \(\large{c_{i,j}}\) としたとき $$\large{c_{i,j}=\sum_{k=1}^{\color{red}{p}}} a_{i\hspace{1pt}k}\hspace{1pt}b_{k\hspace{1pt}j}$$ となる \(\large{n\hspace{1pt}}\)行\(\large{m\hspace{1pt}}\)列の行列 $$\Large{C = \left(\begin{array}{cccc} c_{1,1} & c_{1,2} & \ldots & c_{1,m}\\ c_{2,1} & c_{2,2} & \ldots & c_{2,m}\\ \vdots & \vdots & & \vdots\\ c_{n,1} & c_{n,2} & \ldots & c_{n,m}\\ \end{array} \right)}$$ と定義されます。
行列の積 \(\large{AB}\) の計算は、『行列\(\large{A}\) の列の数』と 『行列\(\large{B}\) の行の数』が一致している必要があります。(上記の定義では、行列\(\large{A}\) の列の数 と行列\(\large{B}\) の行の数 を \(\large{\color{red}{p}}\) としています。)
・2×2行列における行列の積
例えば、\(\large{2 \times 2\hspace{2pt}}\)の行列\(\large{A}\) と 行列\(\large{B}\) の積は、以下のように計算されます。
であるとき \begin{eqnarray} \large AB &=& \large \left(\begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \\ \end{array} \right) \left(\begin{array}{cc} b_{11} & b_{12} \\ b_{21} & b_{22}\\ \end{array} \right) \\[1em] &=&\large \left(\begin{array}{cc} a_{11}b_{11} + a_{12}b_{21} & a_{11}b_{12} + a_{12}b_{22} \\ a_{21}b_{11} + a_{22}b_{21} & a_{21}b_{12} + a_{22}b_{22} \\ \end{array} \right) \\ \end{eqnarray}
上記の \(\large{2 \times 2\hspace{2pt}}\)の行列の積の計算方法を説明します。
まず、行列の積の \(\large{(\color{blue}{1}\color{black}{}\hspace{1pt},\color{red}{1}\color{black}{})}\)成分は、行列\(\large{A}\) の第\(\large{\color{blue}{1}\hspace{1pt}}\)行 と 行列\(\large{B}\) の第\(\large{\color{red}{1}\hspace{1pt}}\)列 の各成分をかけ合わせ、和を計算したものとなります。

次に、行列の積の \(\large{(\color{blue}{1}\color{black}{}\hspace{1pt},\color{red}{2}\color{black}{})}\)成分は、行列\(\large{A}\) の第\(\large{\color{blue}{1}\hspace{1pt}}\)行 と 行列\(\large{B}\) の第\(\large{\color{red}{2}\hspace{1pt}}\)列 の各成分をかけ合わせ、和を計算したものとなります。
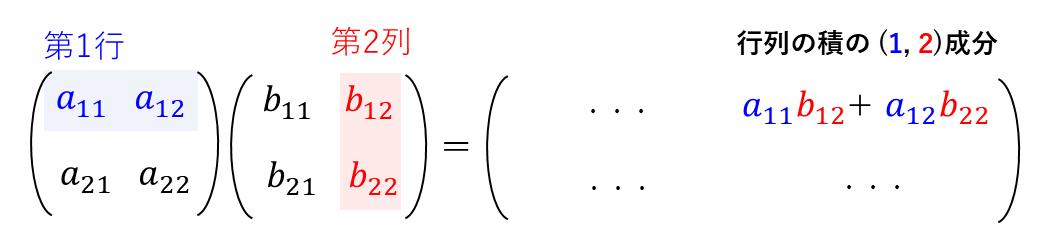
同様に、行列の積の \(\large{(\color{blue}{2}\color{black}{}\hspace{1pt},\color{red}{1}\color{black}{})}\) 成分、\(\large{(\color{blue}{2}\color{black}{}\hspace{1pt},\color{red}{2}\color{black}{})}\) 成分も各成分をかけ合わせ、和を計算したものになります。

・例題
まず、問題の行列の積 \(\large{AB\hspace{2pt}}\)は、『行列\(\large{A}\) の列の数が \(\large{2}\)』 『行列\(\large{B}\) の行の数が \(\large{2}\)』であるため、積を計算することができます。
行列の積 \(\large{AB}\) は以下のように求められます。 \begin{eqnarray} \large AB&\large =&\large \left(\begin{array}{cc} 1 & 2 \\ 3 & -4 \\ \end{array} \right) \left(\begin{array}{cc} 5 & 6 \\ -7 & -8 \\ \end{array} \right)\\[1em] \large &\large =&\large \left(\begin{array}{cc} \hspace{6pt}1\times 5 +2 \times (-7) & 1 \times 6 + 2 \times (-8) \\ 3\times 5 -4 \times (-7) & 3\times 6 -4\times (-8) \\ \end{array} \right)\\[1em] \large &\large =&\large \left(\begin{array}{cc} -9 & -10 \\ 43 & 50 \\ \end{array} \right)\\[1em] \end{eqnarray}
【2】行列の積の結合法則, 分配法則, 交換法則
行列\(\large{A,\hspace{1pt}B,\hspace{1pt}C}\) に対して以下の 結合法則 や 分配法則 が成り立ちます。
・交換法則
ここで、通常の数の積では交換法則が成り立ちますが、一般的に行列では交換法則が成り立ちません。
すなわち、一般的に行列\(\large{A,\hspace{1pt}B}\) に対して 行列の積 \(\large{AB}\) と \(\large{BA}\) は $$\large{AB \neq BA}$$ となります。
交換法則が成り立つこともあり、\(\large{AB = BA}\) が成り立つ場合は、行列\(\large{A,\hspace{1pt}B}\) は交換可能といいます。
・例題
行列\(\large{AB}\) は以下のように計算されます。
\begin{eqnarray} \large AB&\large =&\large \left(\begin{array}{cc} 2 & -1 \\ 1 & 3 \\ \end{array} \right) \left(\begin{array}{ccc} 3 & 2 \\ 1 & 0 \\ \end{array} \right) \\[1em] \large &\large =&\large\left(\begin{array}{cc} 2 \times 3 -1 \times 1& 2 \times 2 -1 \times 0 \\ 1 \times 3 + 3 \times 1 & 1 \times 2 + 3 \times 0 \\ \end{array} \right) \\[1em] &\large =&\large\left(\begin{array}{cc} 5 & 4 \\ 6 & 2 \\ \end{array} \right) \end{eqnarray}また、行列\(\large{BA}\) は以下のように計算されます。
\begin{eqnarray} \large BA&\large =&\large \left(\begin{array}{ccc} 3 & 2 \\ 1 & 0 \\ \end{array} \right) \left(\begin{array}{cc} 2 & -1 \\ 1 & 3 \\ \end{array} \right)\\[1em] \large &\large =&\large\left(\begin{array}{cc} 3 \times 2 +2 \times 1& 3 \times (-1) +2 \times 3 \\ 1 \times 2 + 0 \times 1 & 1 \times (-1) + 0 \times 3 \\ \end{array} \right) \\[1em] &\large =&\large\left(\begin{array}{cc} 8 & 3 \\ 2 & -1 \\ \end{array} \right) \end{eqnarray}上記の計算結果から、行列の積 \(\large{AB}\) と \(\large{BA}\) について $$\large{AB \neq BA}$$ となります。
したがって、行列\(\large{A}\) と 行列\(\large{B}\) の積には交換法則が成り立たないことが分かります。
【3】問題と解き方
のとき 行列の積 \(\large{AB\hspace{1pt},\hspace{3pt}BA}\) は定義されるか
定義される場合は、行列の積を求めよ
【解答と解説】: 問題(1)
のとき 行列の積 \(\large{AB\hspace{1pt},\hspace{3pt}BA}\) は定義されるか
定義される場合は、行列の積を求めよ
【解答と解説】: 問題(2)
のとき 行列の積 \(\large{AB\hspace{1pt},\hspace{3pt}BA}\) は定義されるか
定義される場合は、行列の積を求めよ
【解答と解説】: 問題(3)
のとき 行列の積 \(\large{AB\hspace{1pt},\hspace{3pt}BA}\) は定義されるか
定義される場合は、行列の積を求めよ
【解答と解説】: 問題(4)
のとき 行列の積 \(\large{AB\hspace{1pt},\hspace{3pt}BA}\) は定義されるか
定義される場合は、行列の積を求めよ
【解答と解説】: 問題(5)
問題(1) 1×2行列 と 2×2行列 の積の計算
のとき 行列の積 \(\large{AB\hspace{1pt},\hspace{3pt}BA}\) は定義されるか
定義される場合は、行列の積を求めよ
【解答と解説】
行列の積 \(\large{AB}\) は、『\(\large{1\hspace{1pt}}\)行\(\large{\color{red}{2}\hspace{1pt}}\)列の行列\(\large{A}\)』 と 『\(\large{\color{red}{2}\hspace{1pt}}\)行\(\large{2\hspace{1pt}}\)列の行列\(\large{B}\)』 の積であるので、行列の積は定義されます。(行列\(\large{A}\) の列数 と 行列\(\large{B}\) の行数が等しいため積が定義できる。)
行列の積 \(\large{AB}\) は、以下のように計算されます。
行列の積 \(\large{BA}\) は、『\(\large{2\hspace{1pt}}\)行\(\large{\color{blue}{2}\hspace{1pt}}\)列の行列\(\large{B}\)』 と 『\(\large{\color{blue}{1}\hspace{1pt}}\)行\(\large{2\hspace{1pt}}\)列の行列\(\large{A}\)』 の積であるので、行列の積は定義されません。(行列\(\large{B}\) の列数 と 行列\(\large{A}\) の行数が一致しないため積が定義できない。)
問題(2) 2×3行列 と 3×2行列 の積の計算
のとき 行列の積 \(\large{AB\hspace{1pt},\hspace{3pt}BA}\) は定義されるか
定義される場合は、行列の積を求めよ
【解答と解説】
行列の積 \(\large{AB}\) は、『\(\large{2\hspace{1pt}}\)行\(\large{\color{red}{3}\hspace{1pt}}\)列の行列\(\large{A}\)』 と 『\(\large{\color{red}{3}\hspace{1pt}}\)行\(\large{2\hspace{1pt}}\)列の行列\(\large{B}\)』 の積であるので、行列の積は定義されます。(行列\(\large{A}\) の列数 と 行列\(\large{B}\) の行数が等しいため積が定義できる。)
行列の積 \(\large{AB}\) は、以下のように計算されます。
行列の積 \(\large{BA}\) は、『\(\large{3\hspace{1pt}}\)行\(\large{\color{red}{2}\hspace{1pt}}\)列の行列\(\large{B}\)』 と 『\(\large{\color{red}{2}\hspace{1pt}}\)行\(\large{3\hspace{1pt}}\)列の行列\(\large{A}\)』 の積であるので、行列の積は定義されます。(行列\(\large{B}\) の列数 と 行列\(\large{A}\) の行数が等しいため積が定義できる。)
行列の積 \(\large{BA}\) は、以下のように計算されます。
問題(3) 2×2行列 と 2×3行列 の積の計算
のとき 行列の積 \(\large{AB\hspace{1pt},\hspace{3pt}BA}\) は定義されるか
定義される場合は、行列の積を求めよ
【解答と解説】
行列の積 \(\large{AB}\) は、『\(\large{2\hspace{1pt}}\)行\(\large{\color{red}{2}\hspace{1pt}}\)列の行列\(\large{A}\)』 と 『\(\large{\color{red}{2}\hspace{1pt}}\)行\(\large{3\hspace{1pt}}\)列の行列\(\large{B}\)』 の積であるので、行列の積は定義されます。(行列\(\large{A}\) の列数 と 行列\(\large{B}\) の行数が等しいため積が定義できる。)
行列の積 \(\large{AB}\) は、以下のように計算されます。
行列の積 \(\large{BA}\) は、『\(\large{2\hspace{1pt}}\)行\(\large{\color{blue}{3}\hspace{1pt}}\)列の行列\(\large{B}\)』 と 『\(\large{\color{blue}{2}\hspace{1pt}}\)行\(\large{2\hspace{1pt}}\)列の行列\(\large{A}\)』 の積であるので、行列の積は定義されません。(行列\(\large{B}\) の列数 と 行列\(\large{A}\) の行数が一致しないため積が定義できない。)
問題(4) 1×3行列 と 3×1行列 の積の計算
のとき 行列の積 \(\large{AB\hspace{1pt},\hspace{3pt}BA}\) は定義されるか
定義される場合は、行列の積を求めよ
【解答と解説】
行列の積 \(\large{AB}\) は、『\(\large{1\hspace{1pt}}\)行\(\large{\color{red}{3}\hspace{1pt}}\)列の行列\(\large{A}\)』 と 『\(\large{\color{red}{3}\hspace{1pt}}\)行\(\large{1\hspace{1pt}}\)列の行列\(\large{B}\)』 の積であるので、行列の積は定義されます。(行列\(\large{A}\) の列数 と 行列\(\large{B}\) の行数が等しいため積が定義できる。)
行列の積 \(\large{AB}\) は、以下のように計算されます。
行列の積 \(\large{BA}\) は、『\(\large{3\hspace{1pt}}\)行\(\large{\color{red}{1}\hspace{1pt}}\)列の行列\(\large{B}\)』 と 『\(\large{\color{red}{1}\hspace{1pt}}\)行\(\large{3\hspace{1pt}}\)列の行列\(\large{A}\)』 の積であるので、行列の積は定義されます。(行列\(\large{B}\) の列数 と 行列\(\large{A}\) の行数が等しいため積が定義できる。)
行列の積 \(\large{BA}\) は、以下のように計算されます。
問題(5) 3×3行列 の積の問題
のとき 行列の積 \(\large{AB\hspace{1pt},\hspace{3pt}BA}\) は定義されるか
定義される場合は、行列の積を求めよ
【解答と解説】
行列の積 \(\large{AB}\) は、『\(\large{3\hspace{1pt}}\)行\(\large{\color{red}{3}\hspace{1pt}}\)列の行列\(\large{A}\)』 と 『\(\large{\color{red}{3}\hspace{1pt}}\)行\(\large{3\hspace{1pt}}\)列の行列\(\large{B}\)』 の積であるので、行列の積は定義されます。(行列\(\large{A}\) の列数 と 行列\(\large{B}\) の行数が等しいため積が定義できる。)
行列の積 \(\large{AB}\) は、以下のように計算されます。
行列の積 \(\large{BA}\) は、『\(\large{3\hspace{1pt}}\)行\(\large{\color{red}{3}\hspace{1pt}}\)列の行列\(\large{B}\)』 と 『\(\large{\color{red}{3}\hspace{1pt}}\)行\(\large{3\hspace{1pt}}\)列の行列\(\large{A}\)』 の積であるので、行列の積は定義されます。(行列\(\large{B}\) の列数 と 行列\(\large{A}\) の行数が等しいため積が定義できる。)
行列の積 \(\large{BA}\) は、以下のように計算されます。