転置行列
【1】転置行列とは
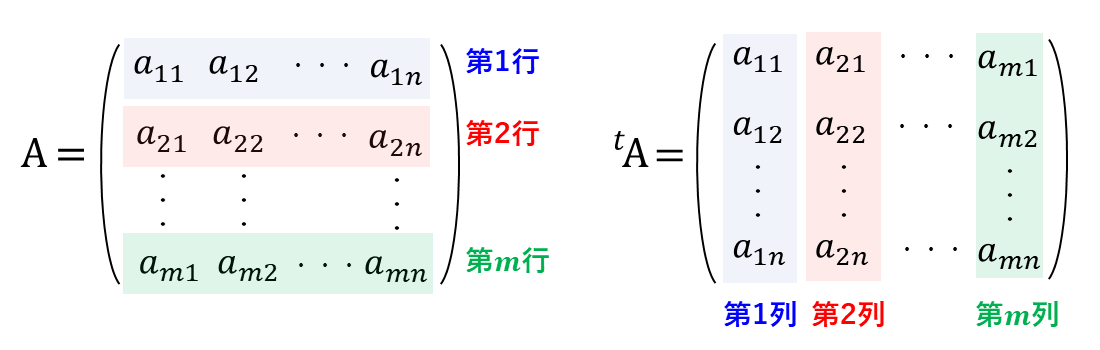
転置行列とは、\(\large{m\hspace{2pt}}\)行\(\large{n\hspace{2pt}}\)列の行列の \(\large{(\hspace{1pt}i\hspace{1pt},\hspace{1pt}j\hspace{1pt})}\)成分\(\large{\hspace{3pt}a_{\hspace{1pt}i,\hspace{1pt}j\hspace{1pt}}}\) と \(\large{(\hspace{1pt}j\hspace{1pt},\hspace{1pt}i\hspace{1pt})}\)成分\(\large{\hspace{3pt}a_{\hspace{1pt}j,\hspace{1pt}i\hspace{1pt}}}\) を入れ替えてできる \(\large{n\hspace{1pt}}\)行\(\large{m\hspace{1pt}}\)列の行列のことです。
転置行列は \(\large{{}^t}A\hspace{1pt},{}^TA\hspace{1pt},A'\hspace{1pt}\) などの記号で表します。
・転置行列の定義
転置行列は、以下のように定義されます。
$$\Large{ {}^tA = \left(\begin{array}{cccc} a_{1,1} & a_{2,1} & \ldots & a_{m,1}\\ a_{1,2} & a_{2,2} & \ldots & a_{m,2}\\ \vdots & \vdots & & \vdots\\ a_{1,n} & a_{2,n} & \ldots & a_{m,n}\\ \end{array} \right)}$$
と定義される\(\large{n\hspace{1pt}}\)行\(\large{m\hspace{1pt}}\)列の行列となる
上記の定義から、行列\(\large{A}\) を 転置行列\(\large{\hspace{2pt}{}^tA}\) に変換するには『第\(\large{1\hspace{1pt}}\)行を第\(\large{1\hspace{1pt}}\)列』『第\(\large{2\hspace{1pt}}\)行を第\(\large{2\hspace{1pt}}\)列』・・・『第\(\large{m\hspace{1pt}}\)行を第\(\large{m\hspace{1pt}}\)列』へと入れ替えることで変換できます。
・2×2行列の転置行列
例えば、\(\large{2 \times 2\hspace{2pt}}\)の行列\(\large{A}\) の転置行列は以下のように求めます。
・例題
行列\(\large{A}\) の転置行列\(\large{\hspace{2pt}{}^tA}\) は『第\(\large{1\hspace{1pt}}\)行を第\(\large{1\hspace{1pt}}\)列』『第\(\large{2\hspace{1pt}}\)行を第\(\large{2\hspace{1pt}}\)列』に入れ替えればよいので $$\large{{}^t A = \left(\begin{array}{cc} 3 & -1 \\ 2 & 4 \\ \end{array} \right) }$$ と求められます。
・3×3行列の転置行列
また、\(\large{3 \times 3\hspace{2pt}}\)の行列\(\large{A}\) の転置行列は以下のように求められます。
・例題
行列\(\large{A}\) の転置行列\(\large{\hspace{2pt}{}^tA}\) は『第\(\large{1\hspace{1pt}}\)行を第\(\large{1\hspace{1pt}}\)列』『第\(\large{2\hspace{1pt}}\)行を第\(\large{2\hspace{1pt}}\)列』『第\(\large{3\hspace{1pt}}\)行を第\(\large{3\hspace{1pt}}\)列』に入れ替えればよいので $$\large{{}^t A = \left(\begin{array}{ccc} 1 & 8 & 3 \\ 2 & -1 & 5 \\ 4 & 6 & 9 \\ \end{array} \right) }$$ と求められます。
【2】転置行列の性質
行列\(\large{A,\hspace{1pt}B}\) が行列、\(\large{k}\) がスカラー量であるとき、以下が成り立ちます。
(4)式では、行列の積\(\large{AB}\) の転置行列\(\large{\hspace{2pt}{}^t (AB)}\) が、行列\(\large{A}\) と 行列\(\large{B}\) の順序を入れ替えた転置行列の積\(\large{\hspace{2pt}{}^tB \hspace{2pt} {}^t\hspace{1pt}A\hspace{2pt}}\)となる点に注意が必要です。
・例題
\(\large{{}^t(AB)}\) は以下のように計算されます。
\begin{eqnarray} \large {}^t(AB)&\large =&\large {}^t\left(\left(\begin{array}{cc} a_{1,1} & a_{1,2} \\ a_{2,1} & a_{2,2} \\ \end{array} \right) \left(\begin{array}{ccc} b_{1,1} & b_{1,2} \\ b_{2,1} & b_{2,2} \\ \end{array} \right)\right) \\[1em] \large &\large =&\large{}^t\left(\begin{array}{cc} a_{1,1}\hspace{2pt} b_{1,1} + a_{1,2} \hspace{2pt} b_{2,1} & a_{1,1}\hspace{2pt} b_{1,2} + a_{1,2}\hspace{2pt} b_{2,2} \\ a_{2,1}\hspace{2pt} b_{1,1} + a_{2,2}\hspace{2pt} b_{2,1}& a_{2,1} \hspace{2pt} b_{1,2} + a_{2,2}\hspace{2pt} b_{2,2} \\ \end{array} \right) \\[1em] &\large =&\large\left(\begin{array}{cc} a_{1,1} \hspace{2pt}b_{1,1} + a_{1,2}\hspace{2pt} b_{2,1} & a_{2,1}\hspace{2pt} b_{1,1} + a_{2,2}\hspace{2pt} b_{2,1}\\ a_{1,1}\hspace{2pt} b_{1,2} + a_{1,2}\hspace{2pt} b_{2,2}& a_{2,1}\hspace{2pt} b_{1,2} + a_{2,2} \hspace{2pt} b_{2,2} \\ \end{array} \right) \\[1em] \end{eqnarray}また、\(\large{{}^t\hspace{1pt}B\hspace{2pt}{}^t\hspace{1pt}A}\) は以下のように計算されます。
\begin{eqnarray} \large {}^t\hspace{1pt}B\hspace{2pt}{}^t\hspace{1pt}A &\large =&\large {}^t\hspace{1pt} \left(\begin{array}{cc} b_{1,1} & b_{1,2} \\ b_{2,1} & b_{2,2} \\ \end{array} \right)\hspace{2pt} {}^t\hspace{1pt}\left(\begin{array}{cc} a_{1,1} & a_{1,2} \\ a_{2,1} & a_{2,2} \\ \end{array} \right)\\[1em] \large &\large =&\large \left(\begin{array}{cc} b_{1,1} & b_{2,1} \\ b_{1,2} & b_{2,2} \\ \end{array} \right)\hspace{2pt} \left(\begin{array}{cc} a_{1,1} & a_{2,1} \\ a_{1,2} & a_{2,2} \\ \end{array} \right) \\[1em] &\large =&\large\left(\begin{array}{cc} a_{1,1} \hspace{2pt}b_{1,1} + a_{1,2}\hspace{2pt} b_{2,1} & a_{2,1}\hspace{2pt} b_{1,1} + a_{2,2}\hspace{2pt} b_{2,1}\\ a_{1,1}\hspace{2pt} b_{1,2} + a_{1,2}\hspace{2pt} b_{2,2}& a_{2,1}\hspace{2pt} b_{1,2} + a_{2,2} \hspace{2pt} b_{2,2} \\ \end{array} \right) \end{eqnarray}上記の計算結果から、 $$\large{{}^t(AB) = {}^t\hspace{1pt}B\hspace{2pt}{}^t\hspace{1pt}A} $$ となります。
【3】対称行列と交代行列
対称行列と交代行列は、転置により定義される行列です。
・対称行列
対称行列とは、転置行列を求めたときに 元の行列と一致する正方行列のことをいいます。
対称行列となる行列\(\large{A}\) は以下の式を満たします。 $$\large{{}^t A = A}$$ \(\large{n\hspace{1pt}}\)次正方行列\(\large{A}\) の \(\large{i\hspace{1pt}}\)行\(\large{j\hspace{1pt}}\)列における成分を \(\large{a_{i\hspace{1pt},\hspace{1pt}j}}\) としたとき、行列\(\large{A}\) が対称行列であれば $$\large{a_{i\hspace{1pt},\hspace{1pt}j} = a_{j\hspace{1pt},\hspace{1pt}i}\hspace{10pt}(1 \leqq i\leqq n\hspace{1pt},\hspace{1pt}1 \leqq j \leqq n)}$$ を満たします。
例えば、以下のような行列\(\large{A}\) は対称行列です。 $$\large{ A = \left(\begin{array}{ccc} 1 & 2 & 3 \\ 2 & -1 & 5 \\ 3 & 5 & 9 \\ \end{array} \right) }$$
・交代行列
交代行列とは、転置行列を求めたときに 元の行列の \(\large{-1\hspace{1pt}}\)倍 になる正方行列のことをいいます。
交代行列となる行列\(\large{A}\) は以下の式を満たします。 $$\large{ {}^t A =-A}$$ \(\large{n\hspace{1pt}}\)次正方行列\(\large{A}\) の \(\large{i\hspace{1pt}}\)行\(\large{j\hspace{1pt}}\)列における成分を \(\large{a_{i\hspace{1pt},\hspace{1pt}j}}\) としたとき、行列\(\large{A}\) が交代行列であれば $$\large{a_{i\hspace{1pt},\hspace{1pt}j} = -a_{j\hspace{1pt},\hspace{1pt}i}\hspace{10pt}(1 \leqq i\leqq n\hspace{1pt},\hspace{1pt}1 \leqq j \leqq n)}$$ となります。
例えば、以下のような行列\(\large{A}\) は交代行列です。 $$\large{{}^t A = \left(\begin{array}{ccc} 0 & -2 & -3 \\ 2 & 0 & -5 \\ 3 & 5 & 0 \\ \end{array} \right) }$$
交代行列では、\(\large{i = j}\) を満たすとき \(\large{a_{i\hspace{1pt},\hspace{1pt}i} = -a_{i\hspace{1pt},\hspace{1pt}i}}\) すなわち \(\large{a_{i,i}=0}\) となります。
したがって、交代行列の対角成分は \(\large{0}\) となります。
【4】問題と解き方
\(\large{A = \left(\begin{array}{cc} \hspace{1pt}4 & 7\hspace{1pt}\\ 1 & 6\\ -9 & 2 \end{array} \right) }\)
【解答と解説】: 問題(1)
\(\large{B = \left(\begin{array}{cccc} \hspace{1pt}4 & 7 & 2 & 10\hspace{1pt}\\ 4 & 1 & 0 & 9\\ 1 & 4 & -7 & 3 \end{array} \right) }\)
【解答と解説】: 問題(2)
\(\large{C = \left(\begin{array}{c} \hspace{1pt}2 \hspace{1pt}\\ 4 \\ 1 \\ -3 \\ \end{array} \right) }\)
【解答と解説】: 問題(3)
問題(1) 2×3行列の転置行列
\(\large{A = \left(\begin{array}{cc} \hspace{1pt}4 & 7\hspace{1pt}\\ 1 & 6\\ -9 & 2 \end{array} \right) }\)
【解答と解説】
行列\(\large{A}\) の転置行列\(\large{{}^t A}\) は『第\(\large{1\hspace{1pt}}\)行を第\(\large{1\hspace{1pt}}\)列』『第\(\large{2\hspace{1pt}}\)行を第\(\large{2\hspace{1pt}}\)列』『第\(\large{3\hspace{1pt}}\)行を第\(\large{3\hspace{1pt}}\)列』に入れ替えればよいので $$\large{{}^t A = \left(\begin{array}{cc} \hspace{1pt}4 & 1 & -9\hspace{1pt}\\ 7 & 6 &2\\ \end{array} \right)}$$ となります。
問題(2) 3×4行列 の転置行列
\(\large{B = \left(\begin{array}{cccc} \hspace{1pt}4 & 7 & 2 & 10\hspace{1pt}\\ 4 & 1 & 0 & 9\\ 1 & 4 & -7 & 3 \end{array} \right) }\)
【解答と解説】
行列\(\large{A}\) の転置行列\(\large{{}^t A}\) は『第\(\large{1\hspace{1pt}}\)行を第\(\large{1\hspace{1pt}}\)列』『第\(\large{2\hspace{1pt}}\)行を第\(\large{2\hspace{1pt}}\)列』『第\(\large{3\hspace{1pt}}\)行を第\(\large{3\hspace{1pt}}\)列』に入れ替えればよいので $$\large{{}^t A = \left(\begin{array}{cc} \hspace{1pt}4 & 4 & 1\hspace{1pt}\\ 7 & 1 &4\\ 2 & 0 &-7\\ 10 & 9 &3\\ \end{array} \right)}$$ となります。
問題(3) 4×1行列 の転置行列
\(\large{C = \left(\begin{array}{c} \hspace{1pt}2 \hspace{1pt}\\ 4 \\ 1 \\ -3 \\ \end{array} \right) }\)
【解答と解説】
行列\(\large{A}\) の転置行列\(\large{{}^t A}\) は『第\(\large{1\hspace{1pt}}\)行を第\(\large{1\hspace{1pt}}\)列』『第\(\large{2\hspace{1pt}}\)行を第\(\large{2\hspace{1pt}}\)列』『第\(\large{3\hspace{1pt}}\)行を第\(\large{3\hspace{1pt}}\)列』『第\(\large{4\hspace{1pt}}\)行を第\(\large{4\hspace{1pt}}\)列』に入れ替えればよいので $$\large{{}^t A = \left(\begin{array}{cccc} \hspace{1pt}2 & 4 & 1 & -3 \hspace{1pt}\\ \end{array} \right)}$$ となります。