一次関数の英語表現
本項では以下の内容を解説しています。
- ・一次関数の式の英語表現
- ・傾きや切片の英語表現
- ・関連用語の一覧
【1】一次関数の英語表現
本章では、一次関数の式や傾き、切片などの英語表現について解説します。
【1-1】一次関数の式の英語表現
一次関数とは、以下の式のように変数xの一次式で表される式です。
上記のような一次関数は英語でlinear functionといいます。
linearとは、線形という意味を持っています。すなわち、xに対するyの変化が一定であることを意味します。
一方、二次関数や三次関数など、xに対するyの変化が一定でない関数はnonlinear functionといいます。
上式では、xは独立変数を意味するindependent variable、yは従属変数を意味するdependent variableともいいます。
また、一次関数のaは係数を意味するcoefficient、bは定数を意味するconstantともいいます。
ここで、一次関数の式『\(\large{y = a x + b}\)』を英語で読むと
『y is equal to a x plus b』もしくは、『y equals a x plus b』といいます。
また、『一次関数のグラフは直線になります。』は英語で『The graph of linear function is a straight line.』と言います。
【1-2】一次関数の傾きの英語表現
上記の一次関数は、xy平面上で傾きを持った直線を表します。
直線の傾きは係数aにより表されます。直線の傾きは英語でslopeもしくはgradientといいます。
係数aが0より大きいとき、直線の傾きが正となり、グラフは右上がりになります。英語では傾きが正であるとき、positive slopeといいます。
一方、係数aが0より小さいとき、傾きは負となり、グラフは右下がりになります。英語では傾きが負であるとき、negative slopeといいます。
以下の図に、右上がりと右下がりの一次関数のグラフを示します。
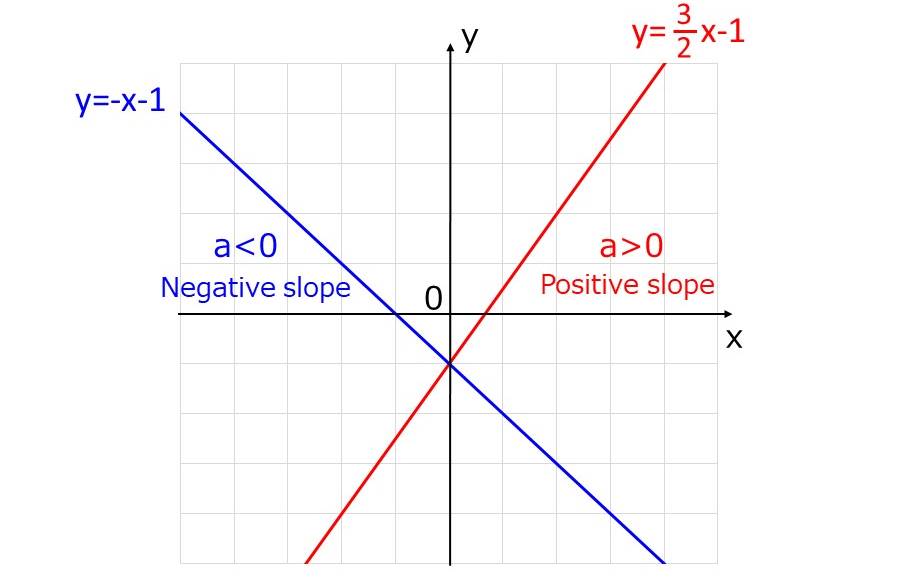
直線の傾きの大きさは、y方向の変化量をx方向の変化量で割った値により求められます。英語では、y方向の変化量をrise、x方向の変化量をrunにより表します。
(差分を意味するΔ(デルタ)を使用し、Δy、Δxと表すこともあります。)
一次関数上の2点\(\large{(x_1,y_1)}\)、\(\large{(x_2,y_2)}\)により直線の傾きを求めると、以下のようになります。
下図に、一次関数の傾きを計算した例を示します。座標(x1,y1)=(0,-1)と(x2,y2)=(2,2)から計算すると、直線の傾きが\(\large{\frac{3}{2}}\)であることが分かります。
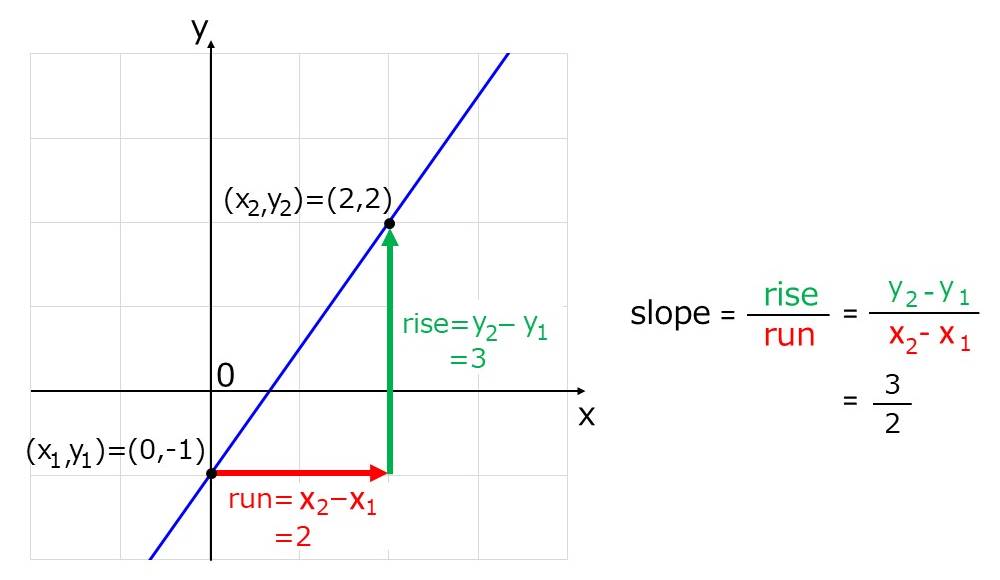
ここで、『一次関数の傾きは、y方向の変化をx方向の変化で割った値により定義されます。』は英語で"The slope of the linear function is defined as the ratio of rise divided by run."と言います。
"A divided by B"は分数\(\Large{\frac{A}{B}}\)を表す表現です。(分数の英語表現は別ページに解説しています。)
【1-3】一次関数の切片の英語表現
切片を英語ではinterceptといいます。
また、y軸上の切片をy-intercept、x軸上の切片をx-interceptといいます。
y軸上の切片(y-intercept)は一次関数の\(\large{x=0}\)の場合であるため、一次関数\(\large{y=ax+b}\)では定数\(\large{b}\)に一致します。
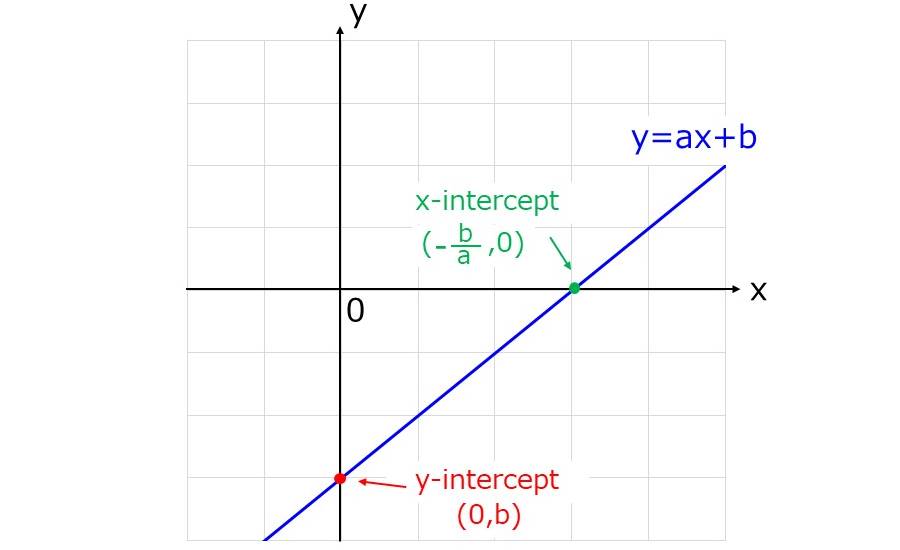
上図のように、一次関数(\(\large{y=ax+b}\))のy軸上の切片の座標は(\(\large{0,b}\))、x軸上の切片の座標は(\(\large{-\frac{b}{a},0}\))となります。
ここで、『y切片を求めるには、一次関数\(\large{y=ax+b}\)に\(\large{x=0}\)を代入します。』は英語で"To find y-intercepts, substitute x=0 into the linear equation y is equal to a x plus b."と言います。
【2】一次関数の英語の用語
一次関数に関する英語の用語を以下の表にまとめています。
| 用語 | 意味 |
|---|---|
| linear function | ・一次関数(線形方程式) |
| nonlinear function | ・非線形方程式 |
| straight line | ・直線 |
| slope | ・傾き |
| gradient | ・傾き |
| rise | ・y方向の変化量 |
| run | ・x方向の変化量 |
| coefficient | ・係数 |
| constant | ・定数 |
| variable | ・変数 |
| independent variable | ・独立変数 |
| dependent variable | ・従属変数 |
| y-intercept | ・y切片(x=0のときのy) |
| x-intercept | ・x切片(y=0のときのx) |
| xy plain | ・xy平面 |
| x-coordinate | ・x座標 |
| y-coordinate | ・y座標 |
| substitute A into B | ・AをBに代入する |