角度の英語表現
本項では以下の内容を解説しています。
- ・鋭角や鈍角など角度の種類
- ・角度の表記方法 (度数法[degree] や 弧度法[radian])
- ・関連用語の一覧
【1】角度の英語表現
本章では、角度に関する英語表現について解説します。
・角度の定義の英語表現
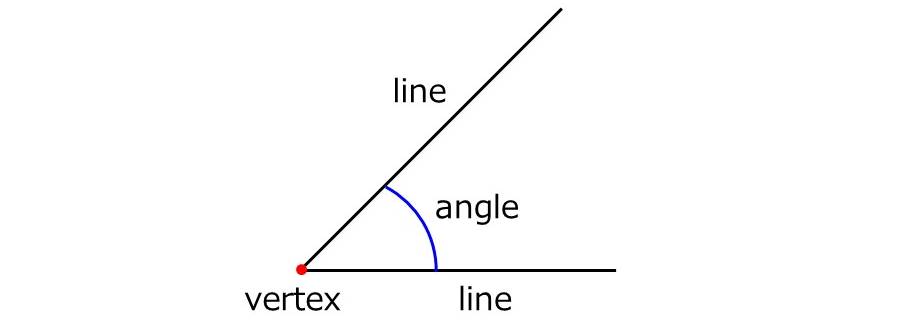
角度は、下図のような2本の直線と頂点により作図されます。英語では、角度をangle、頂点をvertex、直線をlineといいます。(頂点を始点とした半直線の場合は、rayといいます。)
・鋭角,直角,鈍角の英語表現
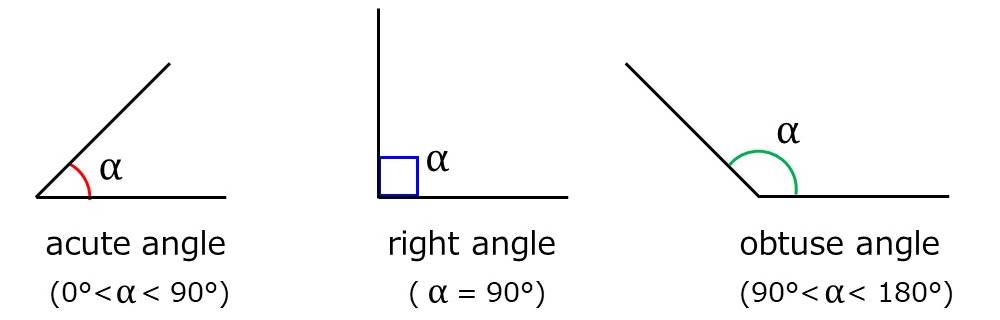
よく使用される角度の種類として、鋭角(acute angle)、直角(right angle)、鈍角(obtuse angle)と言い方があります。
鋭角は、角度が0°より大きく90°より小さい角度に使用します。また、直角は角度が90°のときに使用します。
また、鈍角は角度が90°より大きい場合の角度のことを表します。
・対頂角,同位角,錯角の英語表現
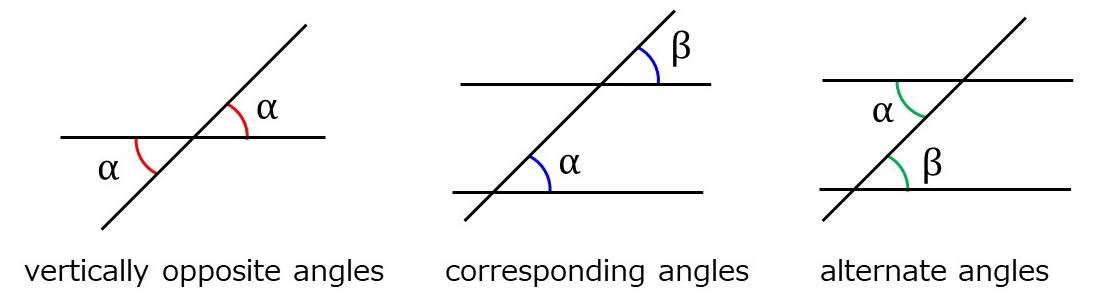
2本の直線が交わり、向かい合った角度のことを対頂角(vertically opposite angles)といいます。対頂角は角度が等しくなる性質があります。
また、3本の直線が交わったときの、同じ方向を向いた角度を同位角(corresponding angles)といいます。2本の直線が平行であるとき、同位角の角度\(\large{\alpha,\beta}\)は等しい値になります。
3本の線が交わったときの、反対方向を向いた角度を錯角(alternate angles)といいます。こちらも、2本の直線が平行であるときに、角度\(\large{\alpha,\beta}\)は等しい値になります。
【2】角度の単位(degree, rad)
角度の単位は、度数法(degree)と弧度法(radian)の2種類が使用されます。
度数法とは、45°や90°など単位に[°](degree)を使用する角度の単位です。また、弧度法とは単位に[rad](radian)を使用する角度の単位です。
また、度数法には、1°未満の角度の表記方法の違いにより、2種類の表記が存在します。
1°未満の角度を十進数により表記する場合をDecimal degrees(DD)といいます。また、六十進数である分と秒で表記する場合をDMS(Degree-Minute-Second)といいます。

本章では度数法の【Ⅰ】十進法(DD)と【Ⅱ】六十進法(DMS)による表記、【Ⅲ】弧度法による表記の3種類の英語表現について解説します。
【Ⅰ】度数法 (十進法,DD)
十進法は10進数のままで角度を表す方法です。英語ではDecimal degreesといい、略してDDともいいます。
十進法で角度を表記すると、20.51°などと表記します。
この記法では、通常の小数点の読み方と同様に、小数点をpoint、小数点以下の数字を1桁づつ言います。
例えば、20.51°は英語でtwenty point five one degreesと読みます。
以下の表に、角度の読み方の例を示します。
| 角度(十進法) | 読み方 |
|---|---|
| 1° | one degree |
| 45° | forty five degrees |
| 90° | ninety degrees |
| 20.51° | twenty point five one degrees |
【Ⅱ】度数法 (六十進法,DMS)
六十進法とは、角度を度分秒により表記する方法です。
度分秒(Degree-Minute-Second)の頭文字からDMSと略されて使われます。
六十進法による表記では、小数点以上の桁は10進数のままで度(degree)で表記し、小数点以下は"1度(degree)=60分(minute)"、"1分(minute)=60秒(second)"と換算して表記します。
例えば、十進法の『20.51°』を六十進法に変換すると『20°30'36"』となります。
英語で20°30'36"を読むと、"twenty degrees thirty minutes (in/and) thirty-six seconds"と言います。
minutesとsecondの間には、inもしくはandを付けることもありますが、省略されることも多いです。
以下の表に、角度の読み方の例を示します。
| 角度(六十進法) | 読み方 |
|---|---|
| 20°30'36" | twenty degrees thirty minutes (in) thirty-six seconds |
| 45°10'5" | forty-five degrees ten minutes (in) five seconds |
| 50°31'2" | fifty degrees thirty-one minutes (in) two seconds |
【Ⅲ】弧度法 (radian)
弧度法(radian)とは、以下の図のような半径\(\large{r}\)の円弧の長さ\(\large{l}\)に対して、\(\large{\theta=l/r}\)により表される角度です。英語で円の半径はradius、円弧の長さはarc lengthといいます。
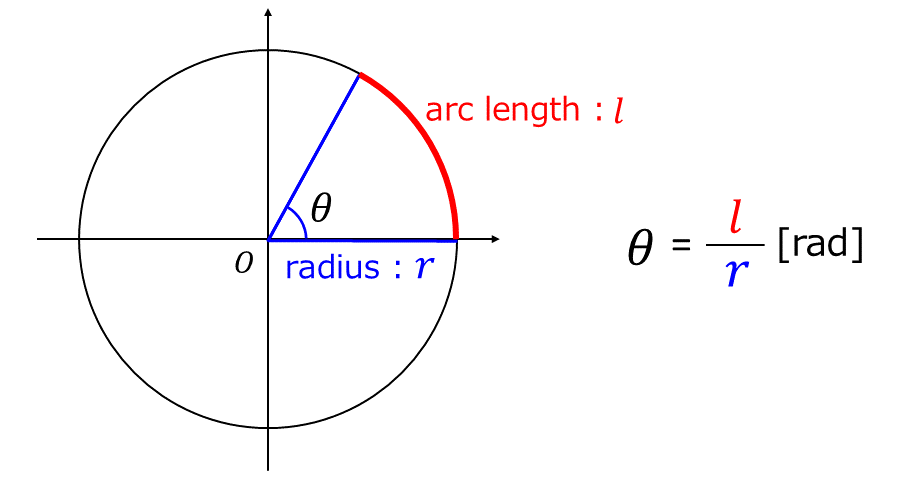
弧度法は単位に[rad]を使用します。例えば、\(\large{\pi}\)/2[rad]は90度を意味します。
\(\large{\pi}\)/2[rad]は英語で"pi over two radians"もしくは、"pi divided by two radians"と言います。
また、270°を意味する3\(\large{\pi}\)/2は、英語で"three pi over two radians"と言います。
(分数\(\Large{\frac{a}{b}}\)は英語で"a over b"や"a divided by b"といいます。分数の英語表現は別ページに解説しています。)
度数法[degree]と弧度法[radian]、弧度法の表記の読み方を以下のようにまとめます。
| 度数法[°] | 弧度法[rad] | 読み方 |
|---|---|---|
| 0 | 0 | zero radians |
| 30 | \(\large{\pi}\)/6 | pi over 6 radians pi divided by 6 radians |
| 45 | \(\large{\pi}\)/4 | pi over 4 radians pi divided by 4 radians |
| 60 | \(\large{\pi}\)/3 | pi over 3 radians pi divided by 3 radians |
| 90 | \(\large{\pi}\)/2 | pi over 2 radians pi divided by 2 radians |
| 180 | \(\large{\pi}\) | pi radians |
| 270 | 3\(\large{\pi}\)/2 | 3 pi over 2 radians 3 pi divided by 2 radians |
| 360 | 2\(\large{\pi}\) | 2 pi radians |
【3】角度に関連する英語の用語のまとめ
角度の種類を説明する英語の用語を以下の表にまとめています。
| 用語 | 意味 |
|---|---|
| acute angle | ・鋭角(0°より大きく90°未満の角度) |
| right angle | ・直角 |
| obtuse angle | ・鈍角(90°より大きく180°未満の角度) |
| straight angle | ・180°の角度 |
| reflex angle | ・180°より大きく360°未満の角度 |
| full rotation angle | ・360°の角度 |
| 90 degrees | ・90° |
次に、直線や図形の角度を説明する英語の用語を以下の表にまとめています。
| 用語 | 意味 |
|---|---|
| vertically opposite angles | ・対頂角 |
| corresponding angles | ・同位角 |
| alternate angles | ・錯角 |
| parallel lines | ・平行線 |
| interior angle | ・内角 |
| exterior angle | ・外角 |
次に、角度の単位を説明する英語の用語を以下の表にまとめています。
| 用語 | 意味 |
|---|---|
| Decimal | ・十進数 |
| radian | ・ラジアン |
| radius | ・半径 |
| arc length | ・円弧の長さ |
上記の用語に関連した例文を紹介します。
『三角形の内角の和は180°です。』を英語で説明すると、以下のようになります。
"The sum of the three interior angles in a triangle is 180 degrees."
『1ラジアンは180°を\(\large{\pi}\)で割った値に等しいです。』を英語で言うと以下のようになります。
"1 radian is equal to 180 degrees divided by pi constant."