数列・級数の英語表現と読み方

本項では以下の内容を解説しています。

• ・等差数列と等比数列の英語表現
• ・級数(シグマ記号)の読み方
• ・関連用語の一覧

【1】数列の英語表現

数列は英語でsequenceといいます。
等差数列はarithmetic sequence、等比数列はgeometric sequenceといいます。

本章では、等差数列と等比数列の英語表現について解説します。

【1-1】等差数列の英語表現

隣接する数字の差分の等しい数列を等差数列といいます。

例えば、以下の数列は、最初の項が2、次以降の項は前の項に3を足した値が並んでいます。
このような数列は、初項\(\hspace{1pt}\large{a_1}\hspace{2pt}\)が2、公差\(\hspace{1pt}\large{d}\hspace{2pt}\)が3の等差数列といいます。

英語で数列の各項をtermといいます。特に、数列の初項を"initial term"もしくは、"first term"といいます。

初項以降の項は、second term、third termと『序数+term』により何番目の項かを言い表します。

また、数列の公差\(\hspace{1pt}\large{d}\hspace{2pt}\)は英語でcommon differenceといいます。

ここで、項の個数が有限である数列を有限数列といいます。有限数列は英語でfinite sequenceといいます。
有限数列である場合、最後の項を特別にlast termという言い方をします。

一方、項の個数が無限である数列を無限数列といいます。無限数列は英語でinfinite sequenceといいます。

【1-2】等差数列の一般項の英語表現

数列の第n項\(\hspace{1pt}\large{a_n}\hspace{2pt}\)をnの式で表すとき、\(\hspace{1pt}\large{a_n}\hspace{2pt}\)を一般項といいます。
一般項は英語で、explicit formulaといいます。もしくは、n番目の項という意味でnth termということもあります。

等差数列の一般解は、初項\(\hspace{1pt}\large{a_1}\hspace{2pt}\)、公差\(\hspace{1pt}\large{d}\hspace{2pt}\)を使用すると以下のような式になります。

ここで、『等差数列の一般項は、"\(\hspace{1pt}\large{a_n = a_1 + (n-1)d}\hspace{2pt}\)"です。』を英語で表すと、『The explicit formula of the arithmetic sequence is "a sub n is equal to a sub 1 plus n minus 1 times d".』といいます。

『a sub n』は下付き文字の\(\hspace{1pt}\large{a_n}\hspace{2pt}\)を言い表す表現です。『sub』は下付き文字であるsubscriptを略した言い方です。

【1-3】等比数列の英語表現

隣接する数字の比が等しい数列を等比数列といいます。
例えば、以下のような等比数列は、初項が3、公比が2の等比数列といいます。

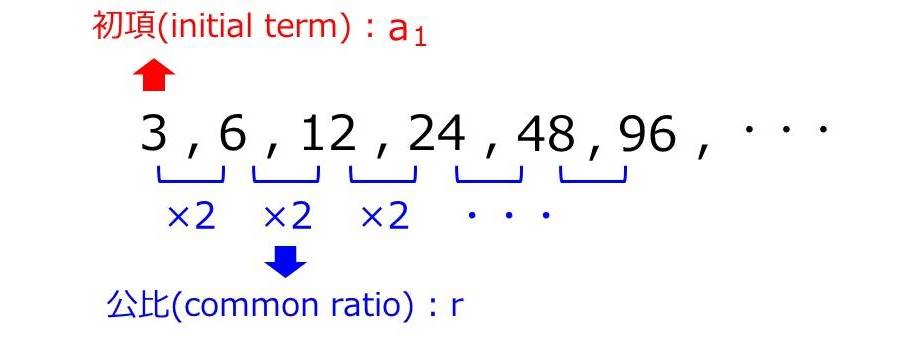
数列の公差は英語でcommon ratioといいます。

等差数列の一般解は、初項\(\hspace{1pt}\large{a_1}\hspace{2pt}\)、公比\(\hspace{1pt}\large{r}\hspace{2pt}\)を使用して以下のような式になります。

ここで、『等比数列の一般項は、"\(\hspace{1pt}\large{a_n = a_1 r^{n-1}}\hspace{2pt}\)"です。』を英語で表すと、『The explicit formula of the geometric sequence is "a sub n is equal to a sub 1 times r to the n minus 1".』といいます。
(r to the nは『rのn乗』を表す用語です。詳しくはべき乗の記事に記載しています。)

【2】数列の級数の英語表現と読み方

数列の項の和を計算したものを級数といいます。級数は英語でseriesといいます。

等差数列の級数を等差級数といい、英語ではarithmetic seriesといいます。
一方、等比数列の級数を等比級数といい、英語ではgeometric sequenceといいます。

また、級数の個数による分類として、無限の個数の数列からなる級数を無限級数といいます。無限級数は英語で、infinite seriesといいます。
一方、ある有限の個数の数列の和を部分和といいます。部分和は英語で、partial sumといいます。

【2-1】シグマ記号の英語での読み方

級数は以下のように、和を表す記号\(\hspace{1pt}\large{\sum}\hspace{2pt}\)によって書き表されます。

記号\(\hspace{1pt}\large{\sum}\hspace{2pt}\)は英語で、"sigma"もしくは、"summation"といいます。

上記のシグマ記号による数列の和\(\hspace{1pt}\large{ \displaystyle \sum_{n=1}^\infty a_n}\hspace{2pt}\)を英語では、"The summation of a sub n as n goes from 1 to infinity"などといいます。
なお、summationの代わりにsum、asの代わりにwhereを使用することもあります。

また、他の例として、以下のようなシグマ記号を使用した数列の和 $$\large{ \displaystyle \sum_{n=1}^5 \frac{1}{n} = 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}}$$ を英語では、"The summation of 1 over n as n goes from 1 to 5"などといいます。

("1 over n"は分数\(\hspace{1pt}\Large{\frac{1}{n}}\hspace{2pt}\)を表す表現です。分数の英語表現は別ページに解説しています。)

【2-2】等差数列の和の英語の読み方

n個の項からなる、初項\(\hspace{1pt}\large{a_1}\hspace{2pt}\)、公差\(\hspace{1pt}\large{d}\hspace{2pt}\)、末項\(\hspace{1pt}\large{a_n}\hspace{2pt}\)の等差数列の和 $$\large { \displaystyle S_n = a_1 + a_2 + a_3 + \cdots +a_n}$$ は以下の式により計算されます。 $$\large { \displaystyle S_n = \frac{a_1 + a_n}{2}n}$$ 上記の数列の和は、英語では"(The partial sum of the arithmetic series) S sub n is equal to sum of the initial term and last term divided dy 2 times n."といいます。

"sum of A and B"はAとBの和を意味する用語です。また、"A divided by B"は分数\(\hspace{1pt}\Large{\frac{A}{B}}\hspace{2pt}\)を表す表現です。

【2-3】等比数列の和の英語の読み方

n個の項からなる、初項\(\hspace{1pt}\large{a_1}\hspace{2pt}\)、公比\(\hspace{1pt}\large{r}\hspace{2pt}\)の等比数列の和 $$\large { \displaystyle S_n = a_1 + ar + a r^2 + \cdots +a r^{n-1}}$$ は\(\hspace{1pt}\large{r \neq 1}\hspace{2pt}\)のとき、以下の式により計算されます。 $$\large { \displaystyle S_n = \frac{a(1-r^n)}{1-r}}$$ 上記の数列の和は、英語では"(The partial sum of the geometric sequence) S sub n is equal to a times 1 minus r to the n divided by 1 minus r."といいます。
(r to the nは『rのn乗』を表す用語です。詳しくはべき乗の記事に記載しています。)

【3】数列・級数の英語用語のまとめ

本項で解説した数列に関連する英語表現の用語の一覧を示します。

また、級数に関連する用語の一覧を示します。

その他、本項で解説した内容以外の、数列や級数によく使用される英語表現の用語の一覧を示します。

---