約数とは | 個数と総和の問題

本項では以下の内容を解説しています。

• ・約数とは
• ・約数の個数と総和
• ・問題と解き方

【1】約数とは

約数とは『ある数を割り切れる整数』のことをいいます。

例えば、\(\large{12\hspace{2pt}}\)の約数を正の範囲で求めると $$\large{1\hspace{2pt},\hspace{2pt}2\hspace{2pt},\hspace{2pt}3\hspace{2pt},\hspace{2pt}4\hspace{2pt},\hspace{2pt}6\hspace{2pt},\hspace{2pt}12}$$ の\(\large{\hspace{1pt}6\hspace{2pt}}\)個となります。

上記のように整数\(\large{\hspace{1pt}N\hspace{2pt}}\)の約数には、\(\large{1\hspace{2pt}}\)と\(\large{\hspace{1pt}N\hspace{2pt}}\)自身も含まれます。

【1-1】約数と素因数分解

約数を求めるときは、先に素因数分解しておくと見通しが良くなります。

素因数分解とは、任意の正の整数を素数の積で書き表すことをいいます。

例えば、\(\large{\hspace{1pt}32\hspace{2pt}}\)を素因数分解すると $$\large{32= 2^5 }$$ となります。

このとき、\(\large{32\hspace{2pt}}\)の約数は『\(\large{\hspace{1pt}2^0\hspace{2pt},\hspace{2pt}2^1\hspace{2pt},\hspace{2pt}2^2\hspace{2pt},\hspace{2pt}2^3\hspace{2pt},\hspace{2pt}2^4\hspace{2pt}\hspace{2pt},\hspace{2pt}2^5\hspace{2pt}}\)』すなわち $$\large{1\hspace{2pt},\hspace{2pt}2\hspace{2pt},\hspace{2pt}3\hspace{2pt},\hspace{2pt}4\hspace{2pt},\hspace{2pt}8\hspace{2pt},\hspace{2pt}16,\hspace{2pt}32}$$ と求められます。
(\(\large{\hspace{1pt}2^0\hspace{2pt}}\)は\(\large{\hspace{1pt}1\hspace{2pt}}\)となります。詳しくは指数法則で解説しています。)

【1-2】2種類の素数で表されるとき

次に\(\large{\hspace{2pt}48\hspace{2pt}}\)を素因数分解すると $$\large{48= 2^4 \times 3^1}$$ となります。

このとき、\(\large{48\hspace{2pt}}\)の約数は『\(\large{\hspace{1pt}2^0\hspace{2pt},\hspace{2pt}2^1\hspace{2pt},\hspace{2pt}2^2\hspace{2pt},\hspace{2pt}2^3\hspace{2pt},\hspace{2pt}2^4\hspace{2pt}\hspace{2pt}}\)』と『\(\large{\hspace{1pt}3^0\hspace{2pt},\hspace{2pt}3^1\hspace{2pt}}\)』から\(\large{\hspace{1pt}1\hspace{2pt}}\)つずつ選んだ積となります。

以下のように 横に\(\large{\hspace{4pt}2^0\hspace{2pt},\hspace{2pt}2^1\hspace{2pt},\hspace{2pt}2^2\hspace{2pt},\hspace{2pt}2^3\hspace{2pt},\hspace{2pt}2^4\hspace{2pt}\hspace{2pt}\hspace{4pt}}\)縦に\(\large{\hspace{4pt}3^0\hspace{2pt},\hspace{2pt}3^1\hspace{4pt}}\)を書いた表を作り、横と縦を掛け合わせた数を入れると約数を簡単に求めることができます。

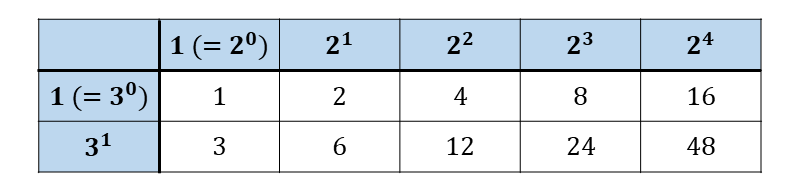
表から\(\large{\hspace{1pt}48\hspace{2pt}}\)の正の約数は $$\large{1\hspace{2pt},\hspace{2pt}2\hspace{2pt},\hspace{2pt}3\hspace{2pt},\hspace{2pt}4\hspace{2pt},\hspace{2pt}6\hspace{2pt},\hspace{2pt}8,\hspace{2pt}12\hspace{2pt},\hspace{2pt}16\hspace{2pt},\hspace{2pt}24,\hspace{2pt}48}$$ と求められます。

・例題1

\(\large{\hspace{2pt}108\hspace{2pt}}\)を素因数分解すると $$\large{108= 2^2 \times 3^3}$$ であることから、横に\(\large{\hspace{4pt}2^0\hspace{2pt},\hspace{2pt}2^1\hspace{2pt},\hspace{2pt}2^2\hspace{4pt}}\)縦に\(\large{\hspace{4pt}3^0\hspace{2pt},\hspace{2pt}3^1\hspace{2pt},\hspace{2pt}3^2\hspace{2pt},\hspace{2pt}3^3\hspace{4pt}}\)を書いた表を作ります。

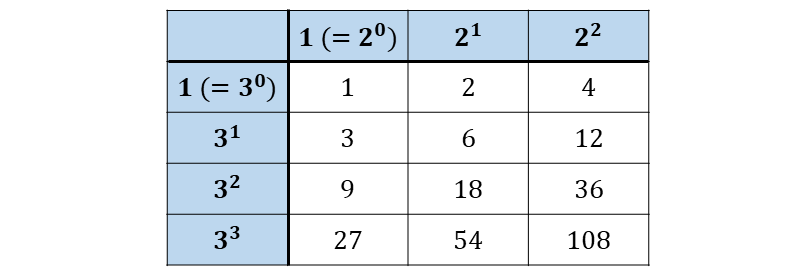
したがって、表の値から\(\large{\hspace{1pt}108\hspace{2pt}}\)の約数は $$\large{1\hspace{2pt},\hspace{2pt}2\hspace{2pt},\hspace{2pt}3\hspace{2pt},\hspace{2pt}4\hspace{2pt},\hspace{2pt}6\hspace{2pt},\hspace{2pt}9,\hspace{2pt}12\hspace{2pt},}$$ $$\large{18\hspace{2pt},\hspace{2pt}27,\hspace{2pt}36\hspace{2pt},\hspace{2pt}54,\hspace{2pt}108}$$ となります。

【1-3】一般化した約数の求め方

素因数分解された結果と約数の関係を一般化すると以下のようになります。
(以下の記号は全て\(\large{\hspace{1pt}1\hspace{2pt}}\)以上の正の整数とします。)

さらに、簡潔に表すと以下のようになります。

【2】約数の個数

本章では、約数の個数と総和の求め方について解説します。

【2-1】約数の個数

先述したように、正の整数\(\large{\hspace{1pt}N\hspace{2pt}}\)が\(\large{\hspace{1pt}N=p^a\hspace{1pt}q^b\hspace{1pt}r^c \cdots\hspace{2pt}}\)と素因数分解されるとき、\(\large{\hspace{1pt}N\hspace{2pt}}\)の約数は以下のように求められます。

正の整数\(\large{\hspace{1pt}N=p^a\hspace{1pt}q^b\hspace{1pt}r^c \cdots\hspace{2pt}}\)の約数の個数を求めたい場合は、上記の集合の要素の数である\(\large{\hspace{1pt}(a+1)\hspace{2pt},\hspace{1pt}(b+1)\hspace{2pt},\hspace{1pt}(c+1)\hspace{2pt}\cdots \hspace{3pt}}\)をかけ合わせることで求められます。

・例題2

\(\large{\hspace{1pt}32\hspace{2pt}}\)の約数の個数を求める場合、\(\large{32\hspace{2pt}}\)の素因数分解の結果が $$\large{32= 2^5 }$$ であることから約数の個数は $$\large{5+1 = 6}$$ となります。

・例題3

\(\large{48\hspace{2pt}}\)の約数の個数を求める場合、\(\large{48\hspace{2pt}}\)の素因数分解の結果が $$\large{48= 2^4 \times 3^1}$$ であることから約数の個数は $$\large{(4+1)\times (1+1) = 10}$$ となります。

【3】約数の総和

正の整数\(\large{\hspace{1pt}N\hspace{2pt}}\)が\(\large{\hspace{1pt}N=p^a\hspace{1pt}q^b\hspace{1pt}r^c \cdots\hspace{2pt}}\)と素因数分解されるとき、\(\large{\hspace{1pt}N\hspace{2pt}}\)の約数の総和は以下のように求められます。

【3-1】総和の式の導出

正の整数\(\large{\hspace{1pt}N\hspace{2pt}}\)が\(\large{\hspace{1pt}N=p^a\hspace{1pt}q^b\hspace{1pt}\hspace{2pt}}\)と素因数分解されるときの総和を求める式を導出します。

\(\large{\hspace{1pt}N=p^a\hspace{1pt}q^b\hspace{1pt}\hspace{2pt}}\)の約数は

　 \(\large{\hspace{1pt}p\hspace{2pt}}\)の累乗の集合\(\large{\{\hspace{2pt}1\hspace{2pt},\hspace{2pt}p^1\hspace{2pt},\hspace{2pt}p^2\hspace{2pt},\hspace{2pt}\cdots \hspace{2pt},\hspace{2pt}p^a\hspace{2pt}\}}\)
　 \(\large{\hspace{1pt}q\hspace{2pt}}\)の累乗の集合\(\large{\{\hspace{2pt}1\hspace{2pt},\hspace{2pt}q^1\hspace{2pt},\hspace{2pt}q^2\hspace{2pt},\hspace{2pt}\cdots \hspace{2pt},\hspace{2pt}q^b\hspace{2pt}\}}\)

から\(\large{\hspace{1pt}1\hspace{2pt}}\)つずつ選んだ積となることから、\(\large{\hspace{1pt}N=p^a\hspace{1pt}q^b\hspace{2pt}}\)の約数は $$\large{1\times 1\hspace{4pt},\hspace{4pt}p\times 1\hspace{4pt},\hspace{4pt}p^2\times 1\hspace{4pt},\hspace{4pt}p^a\times 1\hspace{2pt},}$$ $$\large{1\times q\hspace{4pt},\hspace{4pt}p\times q\hspace{4pt},\hspace{4pt}p^2\times q\hspace{4pt},\hspace{4pt}p^a\times q\hspace{2pt},}$$ $$\large{1\times q^2\hspace{2pt},\hspace{2pt}p\times q^2\hspace{2pt},\hspace{2pt}p^2\times q^2\hspace{2pt},\hspace{2pt}p^a\times q^2\hspace{2pt},}$$ $$\large{\cdots}$$ $$\large{1\times q^b\hspace{2pt},\hspace{2pt}p\times q^b\hspace{2pt},\hspace{2pt}p^2\times q^b\hspace{2pt},\hspace{2pt}p^a\times q^b\hspace{2pt}}$$ となります。

よって、上記の約数の和を求めると

すなわち

となります。

【3-2】等比数列の和の公式の利用

約数の総和を求める式は等比数列の和の公式を利用することで簡単に計算することができます。

初項\(\large{\hspace{1pt}1\hspace{2pt}}\)、公比\(\large{\hspace{1pt}r\hspace{2pt}}\)、項数\(\large{\hspace{1pt}n\hspace{2pt}}\)の等比数列の和の公式は $$\large{\frac{r^n-1}{r-1}}$$ と表されます。

すなわち、\(\large{p\hspace{2pt}}\)の累乗の和\(\large{\hspace{1pt}(1+p+\cdots+p^a)\hspace{2pt}}\) は初項\(\large{\hspace{1pt}1\hspace{2pt}}\)、公比\(\large{\hspace{1pt}p\hspace{2pt}}\)、項数\(\large{\hspace{1pt}a+1\hspace{2pt}}\)の等比数列の和であるから $$\large{1+p+\cdots+p^a = \frac{p^{\hspace{1pt}a+1}-1}{p-1}}$$ となります。

上式を約数の総和を求める式に利用すると、以下のように表されます。

・例題4

\(\large{48\hspace{2pt}}\)の約数の総和を求める場合、\(\large{48\hspace{2pt}}\)の素因数分解の結果が $$\large{48= 2^4 \times 3^1}$$ であることから約数の総和は \begin{eqnarray} \large &&\large (1+2^1+2^2 + 2^3 + 2^4)(1+3^1)\\[0.7em] \large &\large =&\large (1+2+4 +8 + 16)(1+3) \\[0.7em] \large &\large =&\large 31 \times 4 \\[0.7em] \large &\large =&\large 124 \\ \end{eqnarray} と求められます。

・例題4の別解

\(\large{48\hspace{2pt}}\)の約数の総和を等比数列の和の公式を利用すると、以下のようになります。 $$\large{48= 2^4 \times 3^1}$$ であることから約数の総和は \begin{eqnarray} \large &&\large (1+2^1+2^2 + 2^3 + 2^4)(1+3^1)\\[0.7em] \large &\large =&\large \frac{2^{\hspace{1pt}5}-1}{2-1} \cdot \frac{3^{\hspace{1pt}2}-1}{3-1}\\[0.7em] \large &\large =&\large 31 \times 4 \\[0.7em] \large &\large =&\large 124 \\ \end{eqnarray} と求められます。

等比数列の公式を利用した方が、和を計算する手間が省けるため計算が簡単になります。

【4】約数の問題

本章では、約数に関連する問題と解き方について解説します。

解答と解説 : 問題1

解答と解説 : 問題2

解答と解説 : 問題3

解答と解説 : 問題4

解答と解説 : 問題5

解答と解説 : 問題6

問題1.約数を求める問題

問題1の解答

まず、\(\large{500\hspace{2pt}}\)を素因数分解すると $$\large{500 = 2^2 \times 5^3}$$ であることから、\(\large{500\hspace{2pt}}\)の約数は以下のような表を作り求めます。

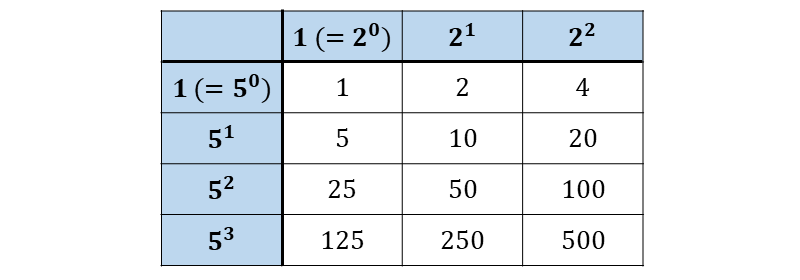
すなわち、上記の表から\(\large{\hspace{2pt}500\hspace{2pt}}\)の約数は $$\large{1\hspace{2pt},\hspace{2pt}2\hspace{2pt},\hspace{2pt}4\hspace{2pt},\hspace{2pt}5\hspace{2pt},\hspace{2pt}10\hspace{2pt},\hspace{2pt}20,\hspace{2pt}25\hspace{2pt},}$$ $$\large{50\hspace{2pt},\hspace{2pt}100,\hspace{2pt}125\hspace{2pt},\hspace{2pt}250\hspace{2pt},\hspace{2pt}500}$$ と求められます。

問題2.約数の個数を求める問題

問題2の解答

まず、\(\large{5000\hspace{2pt}}\)を素因数分解すると $$\large{5000 = 2^3 \times 5^4}$$ であることから\(\large{\hspace{2pt}5000\hspace{2pt}}\)の約数の個数は $$\large{(3+1)\times (4+1) = 20}$$ より\(\large{\hspace{1pt}20\hspace{2pt}}\)個と求めることができます。

問題3.約数の総和を求める問題

問題3の解答

まず、\(\large{5000\hspace{2pt}}\)を素因数分解すると $$\large{5000 = 2^3 \times 5^4}$$ であることから約数の総和は \begin{eqnarray} &&\large (1+2^1+2^2 + 2^3)(1+5^1+5^2+5^3+5^4)\\[0.5em] &\large &\large = (1+2+4 + 8)(1+5+25+125+625)\\[0.7em] \large &\large &\large =15 \times 781\\[0.7em] &\large &\large =11715\\[0.7em] \end{eqnarray} と求められます。

問題3の別解 | 等比数列の和

上記の計算は初項\(\large{\hspace{1pt}1\hspace{2pt}}\)、公比\(\large{\hspace{1pt}r\hspace{2pt}}\)、項数\(\large{\hspace{1pt}n\hspace{2pt}}\)の等比数列の和 $$\large{\frac{r^n-1}{r-1}}$$ を使用することで計算が簡単になります。

\(\large{5000\hspace{2pt}}\)の約数の総和は \begin{eqnarray} &&\large (1+2^1+2^2 + 2^3)(1+5^1+5^2+5^3+5^4)\\[0.5em] &\large &\large =\frac{2^4-1}{2-1} \times \frac{5^5-1}{5-1} \\[0.7em] \large &\large &\large =15 \times 781\\[0.7em] &\large &\large =11715\\[0.7em] \end{eqnarray} と求められます。

問題4.約数の個数から元の値を求める

問題4の解答

ある数\(\large{\hspace{1pt}N\hspace{2pt}}\)が $$\large{N = p^a q^b r^c \cdots}$$ と素因数分解されるとき、その約数の個数は $$\large{(a+1)\hspace{1pt}(b+1)\hspace{1pt}(c+1)\cdots}$$ と求められます。

この関係を利用して約数の個数から元の数\(\large{\hspace{1pt}N\hspace{2pt}}\)を求めます。

素数の種類が\(\large{\hspace{1pt}3\hspace{2pt}}\)種類である場合は、約数の個数が\(\large{\hspace{1pt}10\hspace{2pt}}\)個であるため $$\large{(a+1)\hspace{1pt}(b+1)\hspace{1pt}(c+1)=10}$$ となります。このとき\(\large{\hspace{2pt}10=2\cdot 5\hspace{2pt}}\)と素因数分解されるため、上式を満たす\(\large{\hspace{1pt}1\hspace{2pt}}\)以上の正の整数の組\(\large{\hspace{1pt}(a,b,c)\hspace{2pt}}\)は存在しません。

このように、素数が\(\large{\hspace{1pt}3\hspace{2pt}}\)種類以上のときは、\(\large{1\hspace{2pt}}\)以上の正の整数の組\(\large{\hspace{1pt}(a,b,c,\cdots)\hspace{2pt}}\)は存在しません。

よって、本問では【1】素数が\(\large{\hspace{1pt}1\hspace{2pt}}\)種類の場合 と【2】素数が\(\large{\hspace{1pt}2\hspace{2pt}}\)種類の場合で場合分けします。

【1】素数が\(\large{\hspace{1pt}1\hspace{2pt}}\)種類の場合
素数が\(\large{\hspace{1pt}1\hspace{2pt}}\)種類であるとき、約数の個数が\(\large{\hspace{1pt}10\hspace{2pt}}\)個という条件から $$\large{a+1 = 10}$$ すなわち $$\large{a=9}$$ となります。

したがって、元の数\(\large{\hspace{1pt}N\hspace{2pt}}\)は\(\large{\hspace{1pt}p\hspace{2pt}}\)を素数とすると $$\large{N=p^9}$$ となります。

ここで、\(\large{p=2\hspace{2pt}}\)のとき\(\large{\hspace{1pt}2^9 = 512\hspace{2pt}}\)であるため、\(\large{100\hspace{2pt}}\)より小さい整数\(\large{\hspace{1pt}N=p^a\hspace{2pt}}\)は存在しません。

したがって、素数が\(\large{\hspace{1pt}1\hspace{2pt}}\)種類の場合は条件を満たす整数\(\large{\hspace{1pt}N\hspace{2pt}}\)は存在しません。

【2】素数が\(\large{\hspace{1pt}2\hspace{2pt}}\)種類の場合
素数が\(\large{\hspace{1pt}2\hspace{2pt}}\)種類であるとき、約数の個数が\(\large{\hspace{1pt}10\hspace{2pt}}\)個という条件から $$\large{(a+1)(b+1) = 10}$$ となります。(ただし、\(\large{a \geqq b\hspace{2pt}}\)とする)

\(\large{a \geqq 1 \hspace{2pt},\hspace{2pt}b \geqq 1 \hspace{2pt}}\)の範囲で解くと $$\large{a=4\hspace{2pt},\hspace{3pt}b=1}$$ となります。

したがって、元の数\(\large{\hspace{1pt}N\hspace{2pt}}\)は\(\large{\hspace{2pt}p\hspace{1pt},\hspace{1pt}q\hspace{3pt}}\)を異なる素数とすると $$\large{N=p^4\hspace{1pt} q^1}$$ となります。

\(\large{p \geqq 3\hspace{2pt}}\)であるとき $$\large{p^4\hspace{1pt} q^1 \geqq 3^4 \cdot 2^1 = 162}$$ となり元の数\(\large{\hspace{1pt}N\hspace{2pt}}\)が\(\large{\hspace{1pt}100\hspace{2pt}}\)以下の整数という条件を満たしません。

つまり、\(\large{p=2\hspace{2pt}}\)となります。

また、素数\(\large{\hspace{1pt}q\hspace{2pt}}\)を求めるには、\(\large{1 \leqq 2^4 \cdot q^1 \leqq 100\hspace{3pt}}\)を満たす\(\large{\hspace{1pt}q\hspace{2pt}}\)(ただし、\(\large{q \geqq 3\hspace{2pt}}\))を求めればよいので $$\large{ 2^4\cdot 3^1\hspace{2pt},\hspace{2pt}2^4 \cdot 5}$$ が条件を満たす数となります。

すなわち元の数\(\large{\hspace{1pt}N\hspace{2pt}}\)は $$\large{48\hspace{2pt},\hspace{2pt}80}$$ と求められます。

問題5.約数の個数の条件から元の値を求める

問題5の解答

ある数\(\large{\hspace{1pt}N\hspace{2pt}}\)が $$\large{N = p^a q^b r^c \cdots}$$ と素因数分解されるとき、その約数の個数は $$\large{(a+1)\hspace{1pt}(b+1)\hspace{1pt}(c+1)\cdots}$$ と求められます。

ここで、\(\large{28\hspace{2pt}}\)は\(\large{\hspace{2pt}28=2\cdot 2\cdot 7\hspace{2pt}}\)と素因数分解されるため、\(\large{1\hspace{2pt}}\)以上の正の整数\(\large{\hspace{1pt}(a,b,c, \cdots )\hspace{2pt}}\)が存在するためには \begin{eqnarray} &\large &\large a+1 = 28 \hspace{71pt}\cdots(1)\\[0.7em] &\large &\large (a+1)(b+1) = 28 \hspace{34pt}\cdots(2) \\[0.7em] &\large &\large (a+1)(b+1)(c+1) = 28 \hspace{5pt}\cdots(3) \\ \end{eqnarray} の\(\large{\hspace{1pt}3\hspace{2pt}}\)つの場合に分けられます。

【1】素数が\(\large{\hspace{1pt}1\hspace{2pt}}\)種類の場合
　\(\large{(1)\hspace{2pt}}\)式は素数が\(\large{\hspace{1pt}1\hspace{2pt}}\)種類であることを意味します。

$$\large{a+1 = 28}$$ から $$\large{a = 27}$$ つまり、\(\large{p\hspace{2pt}}\)を素数とすると $$\large{N=p^{27}}$$ となります。

【2】素数が\(\large{\hspace{1pt}2\hspace{2pt}}\)種類の場合
　\(\large{(2)\hspace{2pt}}\)式は素数が\(\large{\hspace{1pt}2\hspace{2pt}}\)種類であることを意味します。

$$\large{(a+1)(b+1) = 28}$$ \(\large{a \geqq b\hspace{2pt}}\)とすると、\(\large{\hspace{1pt}a=13\hspace{2pt},\hspace{2pt}b=1\hspace{3pt}}\)もしくは\(\large{\hspace{1pt}a=6\hspace{2pt},\hspace{2pt}b=3\hspace{3pt}}\)となります。

つまり\(\large{\hspace{3pt}p\hspace{1pt},\hspace{1pt}q\hspace{3pt}}\)を異なる素数とすると $$\large{N=p^{13} q^1\hspace{2pt}}$$ もしくは $$\large{N=p^6 q^3\hspace{2pt}}$$ となります。

【3】素数が\(\large{\hspace{1pt}3\hspace{2pt}}\)種類の場合
　\(\large{(3)\hspace{2pt}}\)式は素数が\(\large{\hspace{1pt}3\hspace{2pt}}\)種類であることを意味します。

$$\large{(a+1)(b+1)(c+1) = 28}$$ \(\large{a \geqq b \geqq c\hspace{2pt}}\)とすると、\(\large{\hspace{1pt}a=6\hspace{2pt},\hspace{2pt}b=1\hspace{2pt},\hspace{2pt}c=1\hspace{3pt}}\)となります。

つまり\(\large{\hspace{3pt}p\hspace{1pt},\hspace{1pt}q\hspace{1pt},\hspace{1pt}r\hspace{3pt}}\)を異なる素数とすると $$\large{N=p^6 q^1 r^1\hspace{2pt}}$$ となります。

ここで、問題では最小の整数を求めるため、\(\large{1\hspace{2pt}}\)以上の正の整数の組み合わせで最小となる\(\large{\hspace{2pt}p=2\hspace{2pt},\hspace{2pt}q=3\hspace{2pt},\hspace{2pt}r=5\hspace{2pt}}\)とします。

上記の数字を当てはめると、候補の数字は\(\large{\hspace{2pt}2^{27}\hspace{2pt},\hspace{2pt}2^{13}\hspace{2pt}3^1\hspace{2pt},\hspace{2pt}2^{6}\hspace{2pt}3^3\hspace{2pt},\hspace{2pt}2^{6}\hspace{2pt}3^1\hspace{2pt} 5^1\hspace{2pt}}\)の\(\large{\hspace{1pt}4\hspace{2pt}}\)個となります。

大小関係を比較すると、明らかに\(\large{\hspace{1pt}2^{6}\hspace{1pt}3^1\hspace{1pt} 5^1\hspace{2pt}}\)が最も小さい数字となります。

したがって、求める最小な整数は\(\large{\hspace{1pt}N=960\hspace{2pt}}\)となります。

問題6.約数の個数と総和から元の値を求める

問題6の解答

ある数\(\large{\hspace{1pt}N\hspace{2pt}}\)が $$\large{N = p^a q^b r^c \cdots}$$ と素因数分解されるとき、その約数の個数は $$\large{(a+1)\hspace{1pt}(b+1)\hspace{1pt}(c+1)\cdots}$$ と求められます。

ここで、\(\large{6\hspace{2pt}}\)は\(\large{\hspace{2pt}6=2\cdot 3\hspace{2pt}}\)と素因数分解されるため、\(\large{1\hspace{2pt}}\)以上の正の整数\(\large{\hspace{1pt}(a,b,c, \cdots )\hspace{2pt}}\)が存在するためには \begin{eqnarray} &\large &\large a+1 = 6 \hspace{71pt}\cdots(1)\\[0.7em] &\large &\large (a+1)(b+1) = 6 \hspace{34pt}\cdots(2) \\[0.7em] \end{eqnarray} の\(\large{\hspace{1pt}2\hspace{2pt}}\)つの場合に分けられます。

【1】素数が\(\large{\hspace{1pt}1\hspace{2pt}}\)種類の場合
　\(\large{(1)\hspace{2pt}}\)式は素数が\(\large{\hspace{1pt}1\hspace{2pt}}\)種類であることを意味します。

$$\large{a+1 = 6}$$ から $$\large{a = 5}$$ つまり、\(\large{p\hspace{2pt}}\)を素数とすると \(\large{N=p^{5}\hspace{2pt}}\) となります。

ここで、\(\large{p=2\hspace{2pt}}\)とおくと約数の総和は \begin{eqnarray} &&\large 1+2^1+2^2 + 2^3+ 2^4 + 2^5\\[0.5em] &\large &\large =\frac{2^6-1}{2-1} \\[0.7em] \large &\large &\large =63\\[0.7em] \end{eqnarray}

また、\(\large{p=3\hspace{2pt}}\)とおくと約数の総和は \begin{eqnarray} &&\large 1+3^1+3^2 + 3^3+ 3^4 + 3^5\\[0.5em] &\large &\large =\frac{3^6-1}{3-1} \\[0.7em] \large &\large &\large =364\\[0.7em] \end{eqnarray}

したがって、素数が\(\large{\hspace{1pt}1\hspace{2pt}}\)種類のときに約数の総和が\(\large{\hspace{1pt}98\hspace{2pt}}\)となる数\(\large{\hspace{1pt}N\hspace{2pt}}\)は存在しません。

【2】素数が\(\large{\hspace{1pt}2\hspace{2pt}}\)種類の場合
　\(\large{(2)\hspace{2pt}}\)式は素数が\(\large{\hspace{1pt}2\hspace{2pt}}\)種類であることを意味します。

$$\large{(a+1)(b+1) = 6}$$ \(\large{a \leqq b\hspace{2pt}}\)とすると、\(\large{\hspace{1pt}a=1\hspace{2pt},\hspace{2pt}b=2\hspace{3pt}}\)となります。

つまり\(\large{\hspace{3pt}p\hspace{1pt},\hspace{1pt}q\hspace{3pt}}\)を異なる素数とすると $$\large{N=p^{1} q^2\hspace{2pt}}$$ と表せます。

ここで、約数の総和が\(\large{\hspace{1pt}98\hspace{2pt}}\)であるため、 $$\large{(1+p)(1+q+q^2) = 98\hspace{5pt}\cdots(3)}$$ を満たします。

また、\(\large{98\hspace{2pt}}\)を素因数分解すると $$\large{98 =2^1 \times 7^2\hspace{5pt}\cdots(4)}$$ となります。

(3),(4)式から\(\large{\hspace{1pt}(1+p)\hspace{2pt}}\)と\(\large{\hspace{1pt}(1+q+q^2)\hspace{2pt}}\)の取る値を表にすると以下のようになります。

素数\(\large{\hspace{1pt}p\hspace{2pt},q\hspace{2pt}}\)の条件を利用し、上記の表から求める数に絞り込みます。

まず、素数\(\large{\hspace{1pt}p\hspace{2pt},q\hspace{2pt}}\)は\(\large{\hspace{1pt}2\hspace{2pt}}\)以上の数であるため、 $$\large{1+p \geqq 3}$$ $$\large{1+q + q^2 \geqq 7}$$ となります。

また、\(\large{1+q + q^2 = 1+q\hspace{1pt}(1+q)\hspace{2pt}}\)であり、\(\large{q\hspace{1pt}(1+q)\hspace{2pt}}\)は隣り合う整数の積であるため偶数となります。

よって、\(\large{1+q + q^2 = 1+q\hspace{1pt}(1+q)\hspace{2pt}}\)は偶数に\(\large{\hspace{1pt}1\hspace{2pt}}\)を足した数であるため、奇数となります。

上記の条件を満たすとき、\(\large{1+p=14\hspace{2pt},\hspace{2pt}1+q + q^2 =7\hspace{2pt}}\)となります。

つまり、\(\large{\hspace{1pt}p=13\hspace{2pt},\hspace{2pt}q=2\hspace{1pt}}\)となります。

したがって、求める正の整数\(\large{\hspace{1pt}N\hspace{2pt}}\)は $$\large{N=13^1\times 2^2 = 52}$$ となります。

---