最大公約数の求め方と問題

本項では以下の内容を解説しています。

• ・最大公約数とは
• ・問題と解き方

【1】最大公約数

本章では、最大公約数について解説します。

【1-1】最大公約数とは

\(\large{\hspace{1pt}2\hspace{2pt}}\)つ以上の数の共通する約数を公約数といいます。

例えば、\(\large{12\hspace{2pt}}\)と\(\large{\hspace{1pt}30\hspace{2pt}}\)の公約数は

\(\large{12\hspace{2pt}}\)の正の約数が $$\large{\color{black}{}1\hspace{2pt},\hspace{2pt}2\hspace{2pt},\hspace{2pt}3\hspace{2pt},\hspace{2pt}4\hspace{2pt},\hspace{2pt}6\hspace{2pt},\hspace{2pt}12}$$ \(\large{30\hspace{2pt}}\)の正の約数が $$\large{\color{black}{}1\hspace{2pt},\hspace{2pt}2\hspace{2pt},\hspace{2pt}3\hspace{2pt},\hspace{2pt}5\hspace{2pt},\hspace{2pt}6\hspace{2pt},\hspace{2pt}10\hspace{2pt},\hspace{2pt}15\hspace{2pt},\hspace{2pt}30}$$ であることから $$\large{\color{black}{}1\hspace{2pt},\hspace{2pt}2\hspace{2pt},\hspace{2pt}3\hspace{2pt},\hspace{2pt}\color{red}{6}\color{black}{}}$$ となります。

公約数のうち、最も大きい公約数のことを最大公約数いいます。
例えば、\(\large{12\hspace{2pt}}\)と\(\large{\hspace{1pt}30\hspace{2pt}}\)の最大公約数は\(\large{\hspace{1pt}6\hspace{2pt}}\)となります。

【1-2】すだれ算による最大公約数の求め方

最大公約数を求める方法として、すだれ算により求める方法があります。

例えば、\(\large{12\hspace{2pt}}\)と\(\large{\hspace{1pt}30\hspace{2pt}}\)の最大公約数をすだれ算により求めます。
まず、最大公約数を求める数字を以下のように横に並べます。

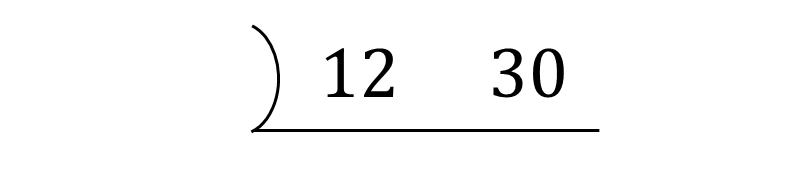
次に、並べた数に共通する素因数で割っていきます。

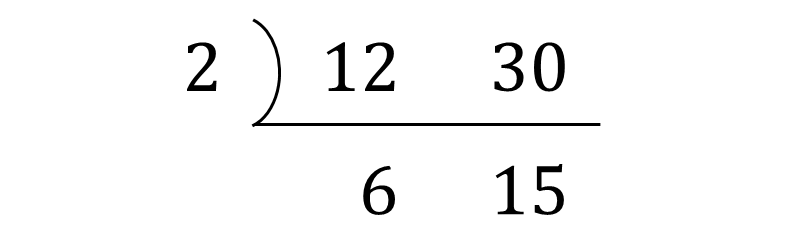
共通する素因数がなくなるまで繰り返し割ります。

最後に、左側に並んだ数字をかけ合わせると、最大公約数が\(\large{\hspace{1pt}6\hspace{2pt}}\)と求められます。

【1-3】素因数分解による最大公約数の求め方

素因数分解を利用することで最大公約数を求めることもできます。

例えば、\(\large{12\hspace{2pt}}\)と\(\large{\hspace{1pt}30\hspace{2pt}}\)の最大公約数を求めると

\(\large{12\hspace{2pt}}\)の素因数分解は $$\large{12 = \color{red}{2}\color{black}{} \times 2 \times \color{red}{3}\color{black}{}}$$ \(\large{30\hspace{2pt}}\)の素因数分解は $$\large{30 = \color{red}{2}\color{black}{} \times \color{red}{3}\color{black}{} \times 5}$$ となります。このとき共通する素因数の積 $$\large{ \color{red}{2}\color{black}{} \times \color{red}{3}\color{black}{} = 6}$$ が最大公約数となります。

先述したすだれ算は大きい数の最大公約数を求める場合に、共通する素因数を見つけるまでに時間がかかることがあります。

一方、素因数分解ではそれぞれの数字を素因数分解すればよいので、より簡単に計算することができます。

【2】最大公約数に関連する問題

本章では、最大公約数に関連する問題と解き方について解説します。

解答と解説 : 問題1

解答と解説 : 問題2

解答と解説 : 問題3

解答と解説 : 問題4

問題1.2つの数の最大公約数を求める問題

問題1の解答

まず、\(\large{120\hspace{2pt}}\)を素因数分解すると $$\large{120 = 2^3 \times 3^1 \times 5^1}$$ \(\large{420\hspace{2pt}}\)を素因数分解すると $$\large{420 = 2^2 \times 3^1 \times 5^1 \times 7^1}$$ となります。

すなわち、共通する素因数の積が最大公約数となるため $$\large{2^2 \times 3^1 \times 5^1 = 60}$$ と求められます。

問題2. 3つの数の最大公約数を求める問題

問題2の解答

まず、\(\large{180\hspace{2pt}}\)を素因数分解すると $$\large{180 = 2^2 \times 3^2 \times 5^1}$$ \(\large{312\hspace{2pt}}\)を素因数分解すると $$\large{312 = 2^3 \times 3^1 \times 13^1}$$ \(\large{336\hspace{2pt}}\)を素因数分解すると $$\large{336 = 2^4 \times 3^1 \times 7^1}$$ となります。

すなわち、共通する素因数の積が最大公約数となるため $$\large{2^2 \times 3^1 = 12}$$ と求められます。

問題3.分数を約分する問題

問題3の解答

約分とは、分母と分子に共通する数で割り、より分母の小さい分数にする操作のことをいいます。

分母と分子が整数の場合、分母と分子の最大公約数で割ることで約分ができます。

本問は分母と分子をそれぞれ素因数分解し、最大公約数を求めて約分します。

・分母を素因数分解する

まず、分母の\(\large{\hspace{1pt}11907\hspace{2pt}}\)を素因数分解します。桁数が大きい整数のため、何の倍数かを判定しながら素因数分解します。

各桁の数を足し合わせると\(\large{\hspace{1pt}1+1+9+0+7 = 18\hspace{2pt}}\)となります。
各桁の数の和が\(\large{\hspace{1pt}9\hspace{2pt}}\)の倍数であるため、\(\large{11907\hspace{2pt}}\)は\(\large{\hspace{1pt}9\hspace{2pt}}\)の倍数であることが分かります。

さらに、\(\large{11907 \div 9 = 1323\hspace{2pt}}\)は、各桁の数を足し合わせると\(\large{\hspace{1pt}1+3+2+3 = 9\hspace{2pt}}\)となり\(\large{\hspace{1pt}9\hspace{2pt}}\)の倍数であることが分かります。

また、\(\large{1323 \div 9 = 147\hspace{2pt}}\)は、各桁の数を足し合わせると\(\large{\hspace{1pt}1+4+7 = 12\hspace{2pt}}\)となり\(\large{\hspace{1pt}3\hspace{2pt}}\)の倍数であることが分かります。

\(\large{147 \div 3 = 49\hspace{2pt}}\)であることから、\(\large{11907\hspace{2pt}}\)を素因数分解すると $$\large{11907 = 3^5 \times 7^2}$$ となります。

・分子を素因数分解する

次に、分子の\(\large{\hspace{1pt}14175\hspace{2pt}}\)を素因数分解します。

各桁の数を足し合わせると\(\large{\hspace{1pt}1+4+1+7+5 = 18\hspace{2pt}}\)となり\(\large{\hspace{1pt}9\hspace{2pt}}\)の倍数であることが分かります。

さらに、\(\large{14175 \div 9 = 1575\hspace{2pt}}\)は、各桁の数を足し合わせると\(\large{\hspace{1pt}1+5+7+5 = 18\hspace{2pt}}\)となり\(\large{\hspace{1pt}9\hspace{2pt}}\)の倍数であることが分かります。

また、\(\large{1575 \div 9 = 175\hspace{2pt}}\)は、一の位が\(\large{\hspace{1pt}5\hspace{2pt}}\)なので\(\large{\hspace{1pt}5\hspace{2pt}}\)の倍数であることが分かります。

\(\large{175 \div 5 = 35\hspace{2pt}}\)であることから、\(\large{14175\hspace{2pt}}\)を素因数分解すると $$\large{14175 = 3^4 \times 5^2 \times 7 }$$ となります。

・分母と分子の最大公約数

すなわち、共通する素因数の積が最大公約数となるため $$\large{3^4 \times 7^1 = 567}$$ と求められます。

したがって、求める約分の結果は分子と分母を\(\large{\hspace{1pt}567\hspace{2pt}}\)で割ればよいので $$\large{\frac{14175}{11907} =\frac{25 \times 567}{21 \times 567}= \frac{25}{21}}$$ と求められます。

問題4.和と最大公約数から元の数を求める

問題4の解答

まず、最大公約数が\(\large{\hspace{1pt}5\hspace{2pt}}\)であることから、 $$\large{a = 5 \hspace{1pt}a' \hspace{2pt},\hspace{3pt}b=5\hspace{1pt}b'}$$ とおきます。

このとき、和が\(\large{\hspace{1pt}75\hspace{2pt}}\)であることから $$\large{5(a' + b') = 75}$$ すなわち $$\large{a' + b' = 15\hspace{5pt}\cdots(1)}$$ となります。

ここで、\(\large{a \leqq b \hspace{2pt}}\)であることから\(\large{\hspace{1pt}a' \leqq b' \hspace{2pt}}\)の条件で(1)式を満たす自然数の組\(\large{\hspace{1pt}(\hspace{1pt}a'\hspace{1pt},\hspace{2pt}b'\hspace{1pt})\hspace{1pt}}\)を求めると $$\large{ (\hspace{1pt}1\hspace{1pt},\hspace{2pt}14\hspace{1pt})\hspace{2pt},\hspace{2pt}(\hspace{1pt}2\hspace{1pt},\hspace{2pt}13\hspace{1pt})\hspace{2pt},\hspace{2pt}(\hspace{1pt}4\hspace{1pt},\hspace{2pt}11\hspace{1pt})\hspace{2pt},\hspace{2pt}(\hspace{1pt}7\hspace{1pt},\hspace{2pt}8\hspace{1pt})}$$ となります。

(このとき\(\large{\hspace{3pt}(\hspace{1pt}3\hspace{1pt},\hspace{2pt}12\hspace{1pt})\hspace{2pt},}\)\(\large{\hspace{2pt}(\hspace{1pt}5\hspace{1pt},\hspace{2pt}10\hspace{1pt})\hspace{2pt},}\)\(\large{\hspace{2pt}(\hspace{1pt}6\hspace{2pt},\hspace{1pt}9\hspace{1pt})\hspace{2pt}}\)は含まれない点に注意が必要です。
最大公約数が\(\large{\hspace{1pt}5\hspace{2pt}}\)という条件から\(\large{\hspace{1pt}a = 5 \hspace{1pt}a' \hspace{2pt},\hspace{3pt}b=5\hspace{1pt}b'\hspace{2pt}}\)とおいているので、\(\large{a'\hspace{1pt},\hspace{1pt}b'\hspace{2pt}}\)は\(\large{\hspace{1pt}1\hspace{2pt}}\)以外の共通する約数がない数字の組み合わせとなります。このような\(\large{\hspace{1pt}1\hspace{2pt}}\)以外の共通する約数がない\(\large{\hspace{1pt}2\hspace{2pt}}\)つの数字のことを互いに素といいます。)

したがって、\(\large{a = 5 \hspace{1pt}a' \hspace{2pt},\hspace{3pt}b=5\hspace{1pt}b'\hspace{3pt}}\)から\(\large{\hspace{1pt}(\hspace{1pt}a\hspace{1pt},\hspace{2pt}b\hspace{1pt})\hspace{1pt}}\)を求めると $$\large{ (\hspace{1pt}5\hspace{1pt},\hspace{2pt}70\hspace{1pt})\hspace{2pt},\hspace{2pt}(\hspace{1pt}10\hspace{1pt},\hspace{2pt}65\hspace{1pt})\hspace{2pt},\hspace{2pt}(\hspace{1pt}20\hspace{1pt},\hspace{2pt}55\hspace{1pt})\hspace{2pt},\hspace{2pt}(\hspace{1pt}35\hspace{1pt},\hspace{2pt}40\hspace{1pt})}$$ となります。

---