最小公倍数の求め方

本項では以下の内容を解説しています。

• ・最小公倍数とは
• ・問題と解き方

【1】最小公倍数

本章では、最小公倍数の意味と求め方について解説します。

【1-1】最小公倍数とは

\(\large{\hspace{1pt}2\hspace{2pt}}\)つ以上の数に共通する倍数を公倍数といいます。

例えば、\(\large{4\hspace{2pt}}\)と\(\large{\hspace{1pt}6\hspace{2pt}}\)の正の倍数を書き並べると

\(\large{4\hspace{2pt}}\)の正の倍数は $$\large{4\hspace{2pt},\hspace{2pt}8\hspace{2pt},\hspace{2pt}12\hspace{2pt},\hspace{2pt}16\hspace{2pt},\hspace{2pt}20\hspace{2pt},\hspace{2pt}24\hspace{2pt},\hspace{2pt}\cdots}$$ \(\large{6\hspace{2pt}}\)の正の倍数は $$\large{6\hspace{2pt},\hspace{2pt}12\hspace{2pt},\hspace{2pt}18\hspace{2pt},\hspace{2pt}24\hspace{2pt},\hspace{2pt}30\hspace{2pt},\hspace{2pt}36\hspace{2pt},\hspace{2pt}\cdots}$$ であることから、\(\large{4\hspace{2pt}}\)と\(\large{\hspace{1pt}6\hspace{2pt}}\)の正の公倍数は $$\large{12\hspace{2pt},\hspace{2pt}24\hspace{2pt},\hspace{2pt}36\hspace{2pt},\hspace{2pt}\cdots}$$ となります。

正の倍数のうち、最も小さい公倍数のことを最小公倍数いいます。
例えば、\(\large{4\hspace{2pt}}\)と\(\large{\hspace{1pt}6\hspace{2pt}}\)の最小公倍数は\(\large{\hspace{1pt}12\hspace{2pt}}\)となります。

【1-2】すだれ算による最小公倍数の求め方

すだれ算を利用することで最小公倍数を簡単に求めることができます。

例えば、\(\large{48\hspace{2pt}}\)と\(\large{\hspace{1pt}60\hspace{2pt}}\)の最小公倍数を求めてみます。

まず、最小公倍数を求める数字を以下のように横に並べます。

次に、並べた数に共通する素因数で割ります。

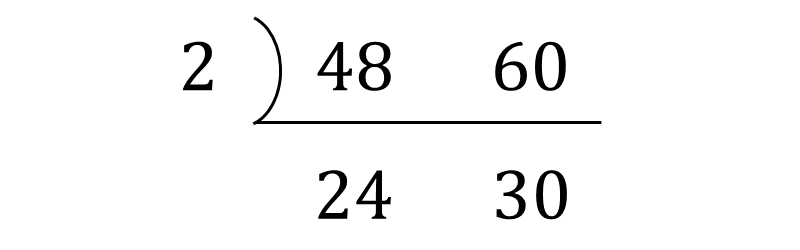
さらに、共通する素因数がなくなるまで繰り返し割ります。

最後に、左側と下側に並んだ数字をかけ合わせることで最小公倍数が求められます。

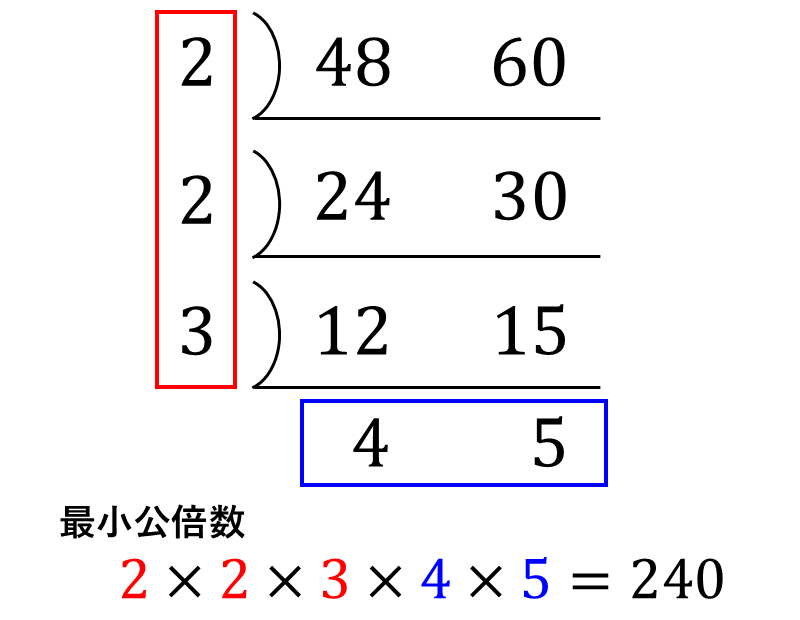
【1-3】素因数分解による最小公倍数の求め方

素因数分解から最小公倍数を求めることもできます。

すだれ算は大きい数どうしの計算をする場合、共通する素因数を見つけるまでに時間がかかる場合があります。

一方、素因数分解はそれぞれの数字に対して計算するため、より簡単に最小公倍数を計算することができます。

素因数分解を利用する場合は、以下の①と②の二つの方法があります。

・①表で整理する方法

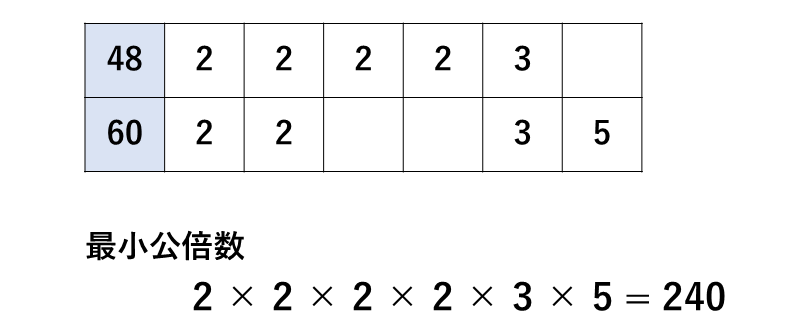
例えば、\(\large{48\hspace{2pt}}\)と\(\large{\hspace{1pt}60\hspace{2pt}}\)の最小公倍数を求めます。

\(\large{48\hspace{2pt}}\)の素因数分解は $$\large{48 = 2 \times 2 \times 2\times 2\times 3}$$ \(\large{60\hspace{2pt}}\)の素因数分解は $$\large{60 =2\times 2 \times 3 \times 5}$$ となります。

それぞれの素因数分解の結果を以下のように表にまとめます。
このとき、同じ数字は数の多い方を選び、全ての数字をかけあわせることで最小公倍数を求めることができます。

・②指数で比較する方法

また、素因数分解の結果を指数で表示して
\(\large{48\hspace{2pt}}\)の素因数分解 $$\large{48 = 2^4 \times 3^1}$$ \(\large{60\hspace{2pt}}\)の素因数分解 $$\large{60 = 2^2 \times 3^1 \times 5^1}$$ のうち指数の大きい方を選びかけ合わせると、最小公倍数を求めることができます。 $$\large{2^4 \times 3^1 \times 5^1 = 240}$$

【2】最小公倍数に関連する問題

本章では、最小公倍数に関連する問題と解き方について解説します。

解答と解説 : 問題1

解答と解説 : 問題2

解答と解説 : 問題3

問題1. 2つの数の最小公倍数を求める問題

問題1の解答

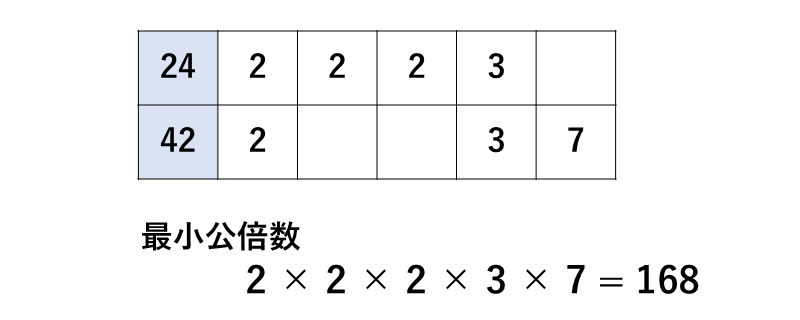
まず、\(\large{24\hspace{2pt}}\)を素因数分解すると $$\large{24 = 2 \times 2\times2\times 3 }$$ \(\large{42\hspace{2pt}}\)を素因数分解すると $$\large{42 = 2 \times 3 \times 7}$$ となります。

それぞれの素因数分解の結果を以下のように表にまとめます。
同じ数字は数の多い方を選び、全ての数字をかけ合わせると、最小公倍数は\(\large{\hspace{1pt}168\hspace{2pt}}\)と求めることができます。

問題1の別解

また、指数を比較する方法を用いると
\(\large{24\hspace{2pt}}\)を素因数分解すると $$\large{24 = 2^3 \times 3^1 }$$ \(\large{42\hspace{2pt}}\)を素因数分解すると $$\large{42 = 2^1 \times 3^1 \times 7^1}$$ となります。

指数の多い数字を選んだ積が最小公倍数となるため $$\large{2^3 \times 3^1 \times 7^1 = 168}$$ と求められます。

問題2. 3つの数の最小公倍数を求める問題

問題2の解答

まず、\(\large{18\hspace{2pt}}\)を素因数分解すると $$\large{18 = 2 \times 3\times 3 }$$ \(\large{42\hspace{2pt}}\)を素因数分解すると $$\large{42 = 2 \times 3 \times 7}$$ \(\large{63\hspace{2pt}}\)を素因数分解すると $$\large{63 = 3 \times 3 \times 7}$$ となります。

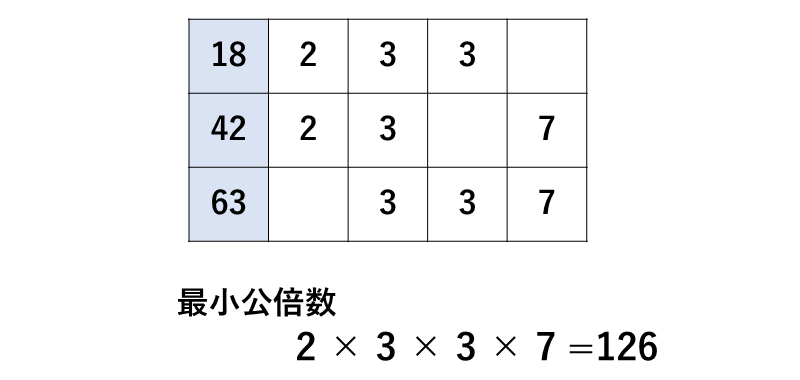
それぞれの素因数分解の結果を以下のように表にまとめます。
同じ数字は数の多い方を選び、全ての数字をかけ合わせると、最小公倍数は\(\large{\hspace{1pt}126\hspace{2pt}}\)と求めることができます。

問題2の別解

また、指数を比較する方法を用いると
\(\large{18\hspace{2pt}}\)を素因数分解すると $$\large{18 = 2^1 \times 3^2 }$$ \(\large{42\hspace{2pt}}\)を素因数分解すると $$\large{42 = 2^1 \times 3^1 \times 7^1}$$ \(\large{63\hspace{2pt}}\)を素因数分解すると $$\large{63 = 3^2 \times 7^1}$$ となります。

指数の多い数字を選んだ積が最小公倍数となるため $$\large{2^1 \times 3^2 \times 7^1 = 126}$$ と求められます。

問題3.最小公倍数から元の数を求める問題

問題3の解答

与えられた最小公倍数の条件を満たすように元の数を求める問題です。
このような問題は、素因数分解を指数で表記する方法から考えます。

\(\large{N\hspace{2pt}}\)を素因数分解した結果が以下のように表されるとします。 $$\large{N = a^{\hspace{1pt}x \hspace{1pt}} b^{\hspace{1pt}y\hspace{1pt}} c^{\hspace{1pt}z} }$$ 元の\(\large{\hspace{1pt}2\hspace{2pt}}\)つの数と最小公倍数の値を整理すると、以下のようになります。

元の数\(\large{\hspace{1pt}4=2^2\hspace{2pt}}\)と\(\large{\hspace{1pt}N = a^{\hspace{1pt}x \hspace{1pt}} b^{\hspace{1pt}y\hspace{1pt}} c^{\hspace{1pt}z} \hspace{2pt}}\)の指数が大きい数字を選んだ積が\(\large{\hspace{1pt}84=2^2\times 3^1 \times 7^1\hspace{2pt}}\)となるような\(\large{\hspace{1pt}N\hspace{2pt}}\)を求めます。

まず、\(\large{a^{\hspace{1pt}x}\hspace{2pt}}\)は\(\large{\hspace{1pt}2^2\hspace{2pt}}\)以下であればよいので\(\large{\hspace{2pt}2^0\hspace{1pt}(\hspace{1pt}=1\hspace{1pt})\hspace{2pt},\hspace{2pt}2^1\hspace{2pt},\hspace{2pt}2^2\hspace{3pt}}\)のいずれかになります。

また、\(\large{b^{\hspace{1pt}y}\hspace{2pt}}\)は\(\large{\hspace{1pt}3^1\hspace{3pt},}\)\(\large{\hspace{3pt}c^{\hspace{1pt}z}\hspace{2pt}}\)は\(\large{\hspace{1pt}7^1\hspace{2pt}}\)である必要があります。

したがって、求める元の数\(\large{\hspace{1pt}N\hspace{2pt}}\)は $$\large{2^0 \times 3^1 \times 7^1\hspace{2pt},\hspace{3pt}2^1 \times 3^1 \times 7^1\hspace{2pt},\hspace{3pt}2^2 \times 3^1 \times 7^1}$$ すなわち $$\large{21\hspace{2pt},\hspace{2pt}42\hspace{2pt},\hspace{2pt}84}$$ となります。

---