光学系の横倍率と縦倍率
本項では、以下の内容について解説します。
- ・【横倍率と縦倍率】の定義と公式
- ・物体位置の変化に対する【横倍率と縦倍率】の変化
【1】横倍率の定義と公式
横倍率(lateral magnification)とは、物体の高さと像の高さの比のことをいいます。
物体の高さを\(\large{Y_1}\)、像の高さを\(\large{Y_2}\)とすると、横倍率\(\large{\beta}\)は以下の式で表せます。
$$\large{\beta=\frac{Y_2}{Y_1}\hspace{20pt}(1)}$$図1に高さ\(\large{Y_1}\)の物体が、厚肉レンズにより高さ\(\large{Y_2}\)の像として結像する様子を図示しています。
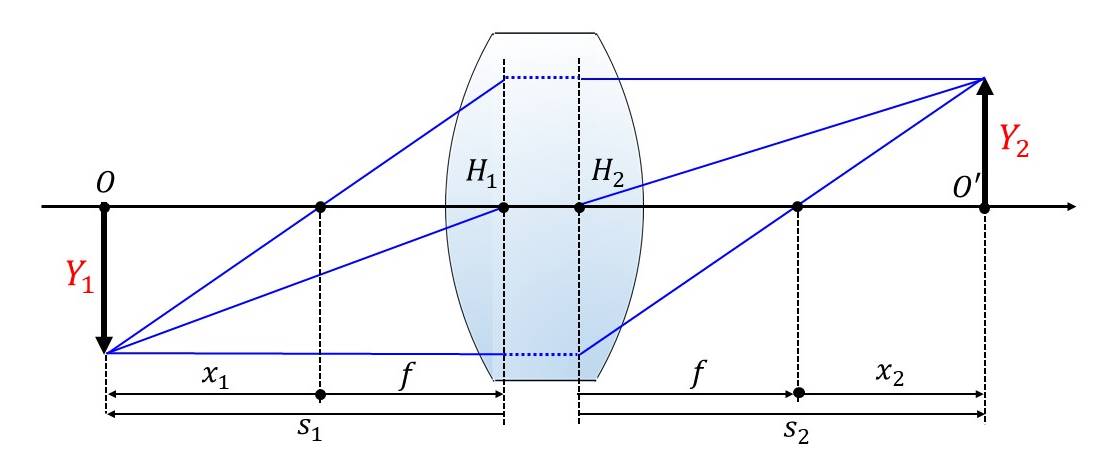
図1の\(\large{H_1}\),\(\large{H_2}\)が主点位置、\(\large{f}\)が焦点距離を表しています。
また、\(\large{x_1}\)が焦点から物体までの距離、\(\large{x_2}\)が焦点から像までの距離、\(\large{s_1}\)が主点から物体、
\(\large{s_2}\)が主点から像の距離を表してます。
図1から、三角形の相似の関係より横倍率\(\large{\beta}\)は主点位置から物体までの距離\(\large{s_1}\)と像位置\(\large{s_2}\)の比で表されることが分かります。
また、横倍率\(\large{\beta}\)は焦点距離\(\large{f}\)と焦点から物体までの距離\(\large{x_1}\)の比、焦点距離\(\large{f}\)と焦点から像までの距離\(\large{x_2}\)の比でも表現されます。
(3)式から、物体位置と結像位置の関係を表現するニュートンの式に変形することができます。 $$\large{x_1x_2=-f^2\hspace{20pt}(4)}$$
【2】縦倍率の定義と公式
縦倍率とは、物体位置の光軸方向の移動に対する像位置の移動の割合のことをいいます。
図2に示すように、物体位置が光軸方向に\(\large{\Delta x_1}\)だけ変化したときの、像位置の光軸方向の変化を\(\large{\Delta x_2}\)とします。
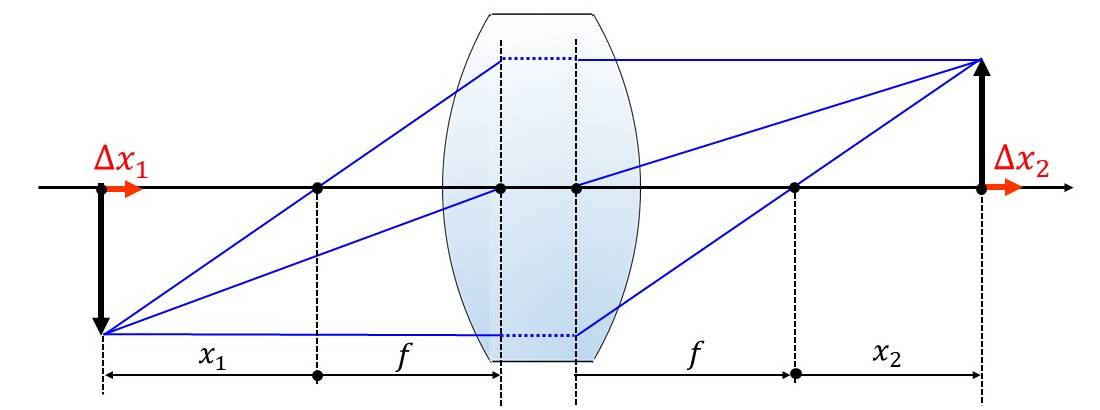
縦倍率\(\large{\alpha}\)を式で定義すると、物体位置が微小変化するときの\(\large{\Delta x_1}\)と\(\large{\Delta x_2}\)の比であるので、(5)式のように表されます。 $$\large{\alpha=\left(\frac{\Delta x_2}{\Delta x_1}\right)_{\Delta x_1\rightarrow0}\hspace{20pt}(5)}$$
結果を先に示すと、縦倍率\(\large{\alpha}\)を焦点からの物体位置\(\large{x_1}\)で表現すると下記のようになります。
また、横倍率が\(\large{\displaystyle \beta=\frac{f}{x_1}}\)であることから、横倍率\(\large{\beta}\)と縦倍率\(\large{\alpha}\)は以下の関係を持ちます。
【2-1】縦倍率の導出
ここで、ニュートンの式((4)式)を利用して、縦倍率((6)式)の導出を行います。
まずは、縦倍率の定義式((5)式)の分子にあたる像位置の変化量\(\large{\Delta x_2}\)を求めます。
ニュートンの式を以下のように変形します。
$$\large{x_2=-\frac{f^2}{x_1}\hspace{20pt}(4)'}$$
(4)'から物体位置が\(\large{\Delta x_1}\)だけ変化したときの、像位置の変化量\(\large{\Delta x_2}\)は以下となります。
\begin{eqnarray}
\large
\Delta x_2&=&-\frac{f^2}{x_1+\Delta x_1}-(-\frac{f^2}{x_1})\
\large
&=&\frac{\Delta x_1f^2}{x_1(x_1+\Delta x_1)}\\
\end{eqnarray}
上式を(5)式に代入すると、以下のようになります。 \begin{eqnarray} \large \alpha&=&\left(\frac{\Delta x_2}{\Delta x_1}\right)_{\Delta x_1\rightarrow0}\\ \large &=&\left(\frac{1}{\Delta x_1}\frac{\Delta x_1f^2}{x_1(x_1+\Delta x_1)}\right)_{\Delta x_1\rightarrow0}\\ \large &=&\left(\frac{f^2}{x_1(x_1+\Delta x_1)}\right)_{\Delta x_1\rightarrow0}\\ \large &=&\frac{f^2}{{x_1}^2}\\ \end{eqnarray}
【3】物体位置に対する横倍率と縦倍率の変化
本章では、これまでに解説した公式を使用して物体位置\(\large{x_1}\)に対する横倍率や縦倍率の変化を説明します。
【3-1】物体が物体側焦点Fより左側に位置するとき
図3に、物体からの光が正の焦点距離fを持つレンズに入射しているとき、物体位置\(\large{x_1}\)が無限に離れた位置から、右側(像側)に移動したときの物体と像の関係を図示しています。
図中では、物体を赤い矢印、像を青い矢印で記載しています。
また、\(\large{F,F'}\)をそれぞれ物体側焦点位置、像側焦点位置、\(\large{H,H'}\)をそれぞれ物体側主点位置、像側主点位置としています。
物体位置\(\large{x_1}\)と像位置\(\large{x_2}\)は、焦点\(\large{F,F'}\)を基準としています。

図3から分かるように物体位置\(\large{x_1}\)が0より小さい範囲にあるときには、横倍率\(\large{\beta}\)は負となり倒立した実像を作ります。
また、物体が物体側焦点Fに近づくほど、実像が大きくなる様子が分かります。
(1)物体が無限に離れている場合
図3の(1)は、物体が無限に離れている場合です。光は焦点\(\large{F'}\)に集光し、横倍率と縦倍率はともに0となります。
(図3の(1)には青い矢印で像が描かれていますが、無限の距離に有限の大きさの物体があるとき、その像は大きさのない点像になります。)
横倍率や縦倍率は、物体距離が遠くなるほど0に漸近していく性質があります。つまり、遠くにある物体ほど像は小さく、また物体の光軸方向の移動量に対して像の移動量は小さくなります。
(3)物体位置が\(\large{x_1 = -f}\)の場合
図3の(3)は、物体位置が\(\large{x_1 = -f}\)の場合です。このとき、縦倍率\(\large{\alpha=1}\)かつ横倍率\(\large{\beta=-1}\)となります。
横倍率\(\large{\beta=-1}\)であることから、物体と等しい大きさの倒立像が作られます。また縦倍率\(\large{\alpha=1}\)であることから、物体が光軸方向に動くとき、同じ割合で像も動きます。
(4)物体位置\(\large{x_1}\)が物体側焦点\(\large{F}\)に近づいたとき
図3の(4)は、物体位置\(\large{x_1}\)が物体側焦点\(\large{F}\)に近づいた(\(x_1\)が0に近づいた)場合です。このとき、横倍率\(\large{\beta=\frac{f}{x_1}}\)、縦倍率\(\large{\alpha=\frac{f^2}{{x_1}^2}}\)であることから、横倍率は負の方向、縦倍率は正の方向に急激に大きくなります。
したがって、この領域では物体位置の変化量に対して、像の大きさや位置が急激に変化します。
【3-2】物体が物体側焦点Fより右側に位置するとき
図4に、物体位置\(\large{x_1}\)が物体側焦点Fよりも右側(\(\large{x_1}\)が0以上)のときの像の様子を図示しています。
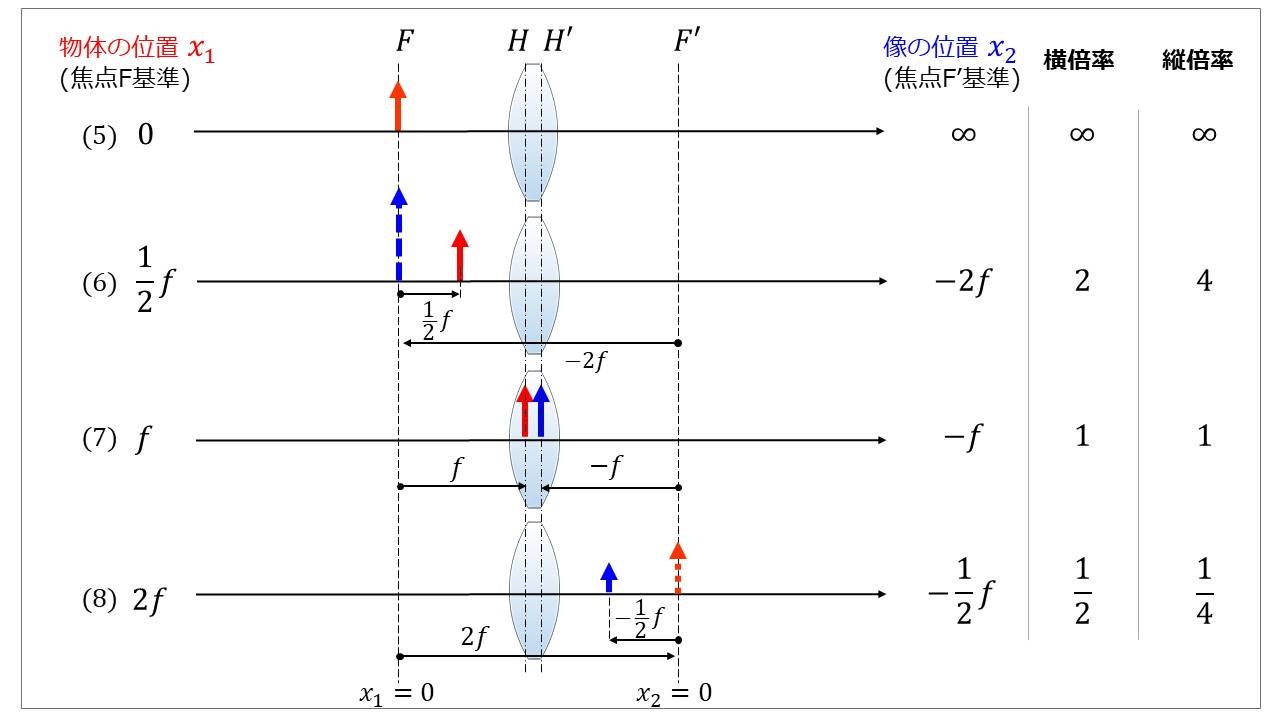
(5)物体位置が物体側焦点Fに一致した場合
図4の(5)は、物体位置\(\large{x_1}\)が焦点Fに一致する場合です。このとき、像はレンズから無限に離れた位置にできると考えます。
(6)物体位置\(\large{x_1}\)が焦点Fよりも内側にある場合
図4の(6)は、物体位置\(\large{x_1}\)が焦点Fよりも内側にある場合です。このとき、物体位置と同じ側に拡大された虚像ができます。
この物体と像の位置関係は、ルーペで物体を拡大して見るときの位置関係に相当します。
(7)物体が主点位置Hに一致した場合
図4の(7)は物体が主点位置Hに一致した場合を表しています。このとき、像側主点位置に倍率1倍で像が形成されます。
これは、主点位置の定義である『物体と像の倍率が1となる軸上共役点』を表した関係です。
(8)物体位置がレンズよりも右側(\(\large{x_1}\)が\(\large{+f}\)以上)に位置する場合
図4の(8)は、物体位置がレンズよりも右側(\(\large{x_1}\)が\(\large{+f}\)以上)に位置する場合を表しています。この状態は虚物体と実像の関係を表しています。
通常は、レンズに対して物体は左側に配置されるため、1枚のレンズによる結像では(8)の状態を考える必要はありません。
しかし、複数のレンズを組み合わせた光学系では、あたかも右側に物体が存在するように像を結ぶ場合があり、(8)の状態となることがあります。 実際には集光していない位置に物体があるとみなすことから、虚物体といいます。
虚物体に関しては、組み合わせレンズの記事の中で説明しています。
参考文献
・(1)岸川利郎『ユーザーエンジニアのための光学入門』(株)オプトロニクス社,平成16年12月18年 第1版9刷発行
・(2)Eugene Heght『原著5版 ヘクト 光学Ⅰ』 2018年10月発行
横倍率、縦倍率の計算などは、(1)『ユーザーエンジニアのための光学入門』の第2章 近軸領域の結像関係(pp.24~30)を参考にした。
虚物体については、(2)『原著5版 ヘクト 光学Ⅰ』の第5章 幾何光学Ⅰ 虚物体(pp.303~306)を参考にした。