-光と光学に関連する用語の解説サイト-

凹面鏡と凸面鏡とは

本項では、以下の内容について解説します。

・凹面鏡と凸面鏡の曲率半径や焦点距離の定義
・凹面鏡と凸面鏡の作図方法
・凹面鏡と凸面鏡の公式の導出
・計算問題

1. 凹面鏡と凸面鏡とは
- 1-1. 曲率半径と焦点距離
- 1-2. 公式と焦点距離
2. 凹面鏡と凸面鏡の作図方法
- 2-1. 凹面鏡の作図方法
- 2-2. 凸面鏡の作図方法
3. 公式の導出
- 3-1. 焦点距離の導出
4. 計算問題
- 4-1. 凹面鏡の結像位置の計算問題
- 4-2. 凸面鏡の結像位置の計算問題

【1】凹面鏡と凸面鏡とは

レンズは光を収束、発散する作用を持ちますが、球面の形状の鏡でもレンズと同様に収束、発散する作用を持たせることができます。

図1(左)に凹面鏡(concave mirror)、図1(右)に凸面鏡(convex mirror)に平行光が入射した様子を図示します。凹面鏡と凸面鏡に平行光が入射した様子

図1.(左)凹面鏡 (右)凸面鏡に平行光が入射した様子

凹面鏡と凸面鏡の違いは、凹面鏡には光を集光する作用があり、凸面鏡には光を発散する作用がある点にあります。

図1に示されているように、凹面鏡では平行光が反射すると、光は焦点$\large{F}$に集光します。つまり、凹面鏡は凸レンズと同じ働きをすることが分かります。

一方、図1右の凸面鏡では平行光が反射された後、あたかも光が焦点$\large{F}$から放出されるように発散します。したがって、凸面鏡は凹レンズと同じ働きをすることが分かります。

【1-1】凹面鏡と凸面鏡の曲率半径と焦点距離

図1の$\large{R}$は、凹面鏡と凸面鏡の曲率半径を表します。
曲率半径$\large{R}$は、球面の頂点$\large{V}$から、球面の中心$\large{C}$までの距離で定義されます。

光軸の右向きを正とすると、凹面鏡の曲率半径$\large{R}$は負、凸面鏡の曲率半径$\large{R}$は正の符号となります。

図1のように、平行光を入射したときに集光する位置を焦点$\large{F}$といいます。
また、焦点距離$\large{f}$は球面の頂点$\large{V}$から、焦点$\large{F}$までの距離で定義されます。

【1-2】凹面鏡と凸面鏡の公式と焦点距離

曲率半径$\large{R}$の凹面鏡(もしくは凸面鏡)から、位置$\large{s}$に物体があり、その像が位置$\large{s'}$に結像するときの公式は以下の式となります。

【凹面鏡と凸面鏡の公式】

$\large{ \displaystyle \frac{1}{s}+\frac{1}{s'}=\frac{2}{R}}$

また、焦点距離の大きさは、曲率半径$\large{R}$の半分の大きさになります。

【凹面鏡と凸面鏡の焦点距離】

$\large{ \displaystyle f = \frac{R}{2}}$

公式の導出方法と、公式を利用した計算問題については後述しています。

【2】凹面鏡と凸面鏡の作図方法

本章では、凹面鏡と凸面鏡で作図を行う方法について解説します。

【2-1】凹面鏡の作図方法

凹面鏡は以下のように光線を描くことで作図をすることができます。

(Ⅰ)光軸に対して平行に入射した光線は、焦点$\large{F}$を通る経路に反射されます。
また、焦点$\large{F}$を通過して入射した光線は、光軸に平行な方向に反射されます。

(Ⅱ)球面の中心$\large{C}$を通過した光線は、再度同じ経路となるように反射されます。

(Ⅲ)球面の頂点$\large{V}$に入射した光線は、入射光線と光軸のなす角度と同じ角度で反射され、光軸に対して対称となります。凹面鏡の作図の方法の解説図

図2.凹面鏡の作図の方法

(Ⅱ)は、球面の中心$\large{C}$を通過した光線が、球面の接線に対して垂直に入射することから、同じ方向に反射されると考えることができます。

また、(Ⅲ)は球面の頂点$\large{V}$の接線に対して、反射の法則が成り立つことから同じ角度で反射されます。 (光の反射についてはこちらで解説しています。)

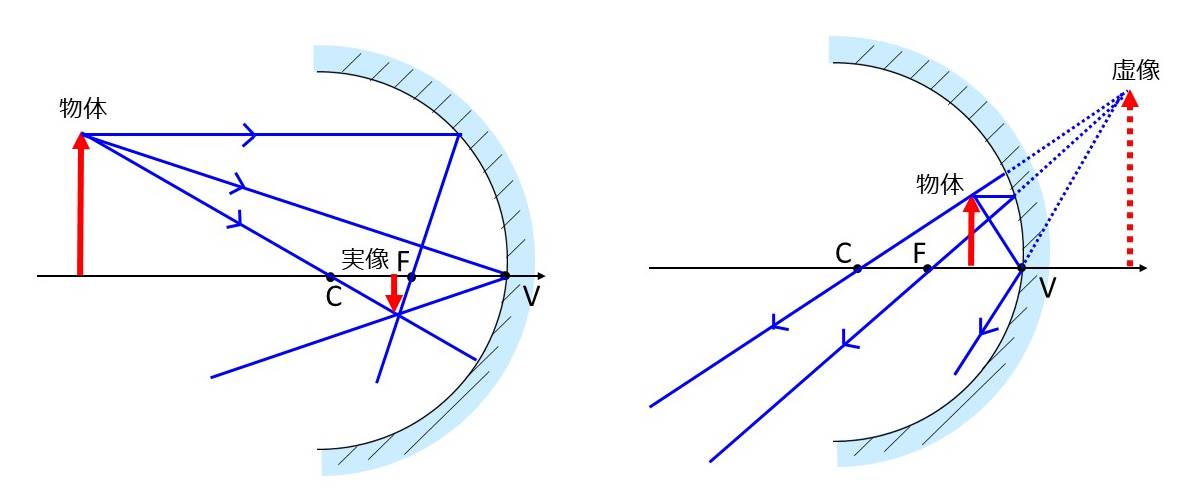
図3に上記の作図方法により、物体を凹面鏡により結像した図を示します。凹面鏡による結像の作図方法(実像と虚像)

図3.凹面鏡による結像の作図(左図)実像(右図)虚像

凹面鏡では、物体の位置により実像もしくは虚像が結像されます。

物体が焦点位置$\large{F}$より凹面鏡から離れた位置にあるとき、図3の左のように実像となります。
一方、物体が焦点位置$\large{F}$より凹面鏡に近い位置にあるとき、図3の右のように虚像となります。

【2-2】凸面鏡の作図方法

(Ⅰ)光軸に平行に入射した光線は、あたかも焦点$\large{F}$から射出された光線のような経路となります。また、焦点$\large{F}$に向かう方向に入射した光線は、反射された後に光軸に平行な光線となります。

(Ⅱ)球面の中心$\large{C}$を通過した光線は、同じ経路を反対方向に反射されます。

(Ⅲ)球面の頂点$\large{V}$に入射した光線は、入射光線と光軸のなす角度と同じ角度で反射され、光軸に対して対称となります。凸面鏡の作図の方法の解説図

図4.凸面鏡の作図の方法

図5に上記の作図方法により、凸面鏡の前に物体を置いたときの光線の様子を図示します。凸面鏡による結像の作図方法(実像と虚像)

図5.凸面鏡による虚像の作図

図5のように、凸面鏡では物体の位置に関わらず、鏡の中に虚像が生成されます。

【3】凹面鏡と凸面鏡の公式の導出

本章では、凹面鏡と凸面鏡の公式を導出します。

図6に示されているように、曲率半径$\large{R}$の凹面鏡から、$\large{s}$の位置に物体があり、その像が$\large{s'}$の位置に結像したとします。
このときの結像位置$\large{s'}$を求める公式を導出します。
凹面鏡と凸面鏡の公式の導出の説明図

図6.凹面鏡の公式の導出

まず、反射の法則から、球面上の点$\large{P}$において入射角と反射角は等しくなるため、$\large{\theta_i = \theta_r}$を満たします。

このとき、三角形OPO'に対して二等分線の定理が成り立つため、以下の式が成り立ちます。 $$\large{\frac{\overline{PO}}{\overline{PO'}} = \frac{\overline{OC}}{\overline{O'C}}\hspace{20pt}(1)}$$

ここで、図6より以下の関係が成り立ちます。 $$\large{\overline{OC}=s-R}$$ $$\large{\overline{O'C}=R-s'}$$

また、$\large{\overline{PQ}=\overline{PO} \sin \theta_1}$、$\large{\overline{PQ}=\overline{PO'} \sin \theta_2}$が成り立つため、以下の関係が成り立ちます。 $$\large{\frac{\overline{PO}}{\overline{PO'}} = \frac{\sin \theta_2}{\sin \theta_1}}$$

したがって、(1)式から以下の関係を導くことができます。 $$\large{\frac{\sin \theta_2}{\sin \theta_1} = \frac{s-R}{R-s'}\hspace{20pt}(2)}$$

ここで、(2)式を近軸光線(光線の高さが極限まで光軸に近い位置を通るとした近似)として近似すると、$\large{\sin \theta_1, \sin \theta_2}$は以下のようになります。 $$\large{\sin \theta_1 \approx \frac{\overline{PQ}}{s} }$$ $$\large{\sin \theta_2 \approx \frac{\overline{PQ}}{s'} }$$

上式から、(2)式を変形すると以下のようになります。 $$\large{\frac{s}{s'}=\frac{s-R}{R-s'}}$$ 上式を整理することで、凹面鏡(凸面鏡)の公式を求めることができます。

【凹面鏡と凸面鏡の公式】

$\large{ \displaystyle \frac{1}{s}+\frac{1}{s'}=\frac{2}{R}\hspace{20pt}(3)}$

凹面鏡も凸面鏡も同じ式(3)により結像関係を計算することができます。

【3-1】凹面鏡の焦点距離の導出

ここで、凹面鏡と凸面鏡の公式から焦点距離$\large{f}$を導出すると、物体位置が$\large{s=-\infty}$であるときの結像位置$\large{s'}$が焦点距離$\large{f}$であるため、以下となります。 $$\large{\frac{1}{f} = \frac{2}{R}}$$ $$\large{f=\frac{R}{2}}$$

この関係を使用して(3)式を整理すると、以下のようになります。

【凹面鏡と凸面鏡の公式】

$\large{ \displaystyle \frac{1}{s}+\frac{1}{s'}=\frac{1}{f}\hspace{20pt}(4)}$

焦点距離は『主点$\large{H}$から焦点$\large{F}$までの距離』で定義されますが、凹面鏡と凸面鏡の主点は球面の頂点$\large{V}$と一致します。

凹面鏡の場合、焦点$\large{F}$が球面の頂点$\large{V}$より前側にあるため、焦点距離$\large{f}$は負の値となります。
一方、凸面鏡の場合、焦点$\large{F}$が球面の頂点$\large{V}$より後側にあるため、焦点距離$\large{f}$は正の値となります。