√(-x^2+2x)の定積分
◆第問目!
$${\large \int_0^2 \sqrt{-x^2+2x} \hspace{1pt}dx}$$
関数\(\hspace{1pt}y=\sqrt{-x^2+2x}\hspace{1pt}\)がどのような図形を表すのかを考えます
【解答のポイント】
本問は、まず関数\(\hspace{1pt}y=\sqrt{-x^2+2x}\hspace{1pt}\)がどのような図形を表すのかを考えてみます。
そこで、\(y=\sqrt{-x^2+2x}\hspace{1pt}\)の両辺を二乗し、平方完成して整理します。
【解答】
関数 \({y=\sqrt{-x^2 +2x}}\) の両辺を二乗し、平方完成すると
すなわち、 $${(x-1)^2 + y^2 = 1}$$ となります。
上式は半径が\({\hspace{1pt}1\hspace{1pt}}\)、中心が \({(\hspace{1pt}1\hspace{1pt},\hspace{2pt}0\hspace{1pt})}\) であるような円の上半分 \({(\mathrm{y \geqq 0})}\) を表します。
よって、問題の定積分 \(\displaystyle{\int_{0}^{2} \sqrt{-x^2 +2x} \hspace{1pt}\hspace{1pt} dx}\) の表す領域を図示すると、以下の青色で示す範囲となります。
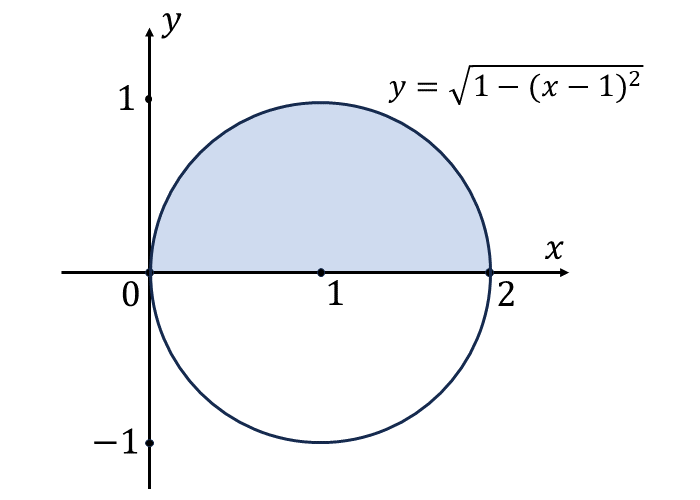
したがって、問題の定積分は半径\({\hspace{1pt}1\hspace{1pt}}\)の円の上半分の面積を表すため $${\int_{0}^{2} \sqrt{-x^2 +2x} \hspace{1pt}\hspace{1pt} dx = \frac{\pi}{2}}$$ となります。
【別解】
計算量が多くなりますが、積分の計算をして求めることもできます。
まずルートの中を平方完成します。
上式を置換積分法により変数を置き換えて計算します。
中心が原点の円の積分 \(\displaystyle{\int_{-1}^{1} \sqrt{1-x^2} \hspace{1pt}\hspace{1pt} dx}\) では \({x = \sin t}\) と置き換え積分することから類推し、\({x-1 = \sin t}\) とおいて積分します。
変数\({x}\) の区間\({\hspace{1pt}[\hspace{1pt}0\hspace{1pt},\hspace{2pt}2\hspace{1pt}]}\) に対応する 変数\({t}\) の区間 を求めます。
| \({x}\) | \(\displaystyle{0 \to 2}\) |
|---|---|
| \({t}\) | \(\displaystyle{-\frac{\pi}{2} \to \frac{\pi}{2}}\) |
ここで、\({x= \sin t}\) の両辺を \({t}\) で微分すると、三角関数の微分公式から $${\frac{dx}{dt} = \cos t}$$ となります。
すなわち、\(\displaystyle{dx = \cos t \hspace{1pt} dt}\) と表せます。
したがって、問題の定積分は以下のように計算されます。
(\(-\frac{\pi}{2} \leqq t \leqq \frac{\pi}{2}\hspace{1pt}\)において、\(\cos t \geqq 0\hspace{1pt}\)であることから、\(|\cos t| = \cos t\hspace{1pt}\)となります。)
ここで、半角の公式 $${\cos^2 t = \frac{1+\cos 2t}{2}}$$ から式変形すると、
以上から $${\int_{0}^2 \sqrt{-x^2+2x} \hspace{1pt} dx = \frac{\pi}{2} }$$ と求めることができます。
【関連するページ】
・円の面積の積分