放物線と直線に囲まれた面積の最小値

【解答のポイント】

式に文字を含む場合は、交点の\({\hspace{1pt}x\hspace{2pt}}\)座標を求めて定積分を計算しようとすると、計算が煩雑になります。

そこで、曲線 \({y=ax^2+bx+c}\) と 直線との交点を \({x=\alpha,\hspace{2pt}\beta}\) としたとき囲まれる面積\({\hspace{1pt}S\hspace{2pt}}\)を求める1/6公式
$$\displaystyle{S = \frac{|a|}{6}(\beta-\alpha)^3}$$ から『\({\beta - \alpha\hspace{2pt}}\)が最小値』 のとき 『面積\({\hspace{1pt}S\hspace{2pt}}\)が最小値』となることを利用します。

【解答】

まず、\({y=x^2+2x-3}\) と 直線 \({y=mx +2}\) が\({\hspace{1pt}2\hspace{2pt}}\)つの交点を持つための条件を求めます。

曲線と直線の式から\({\hspace{2pt}y\hspace{2pt}}\)を削除し、交点の\({x\hspace{1pt}}\)座標の満たす式を求めると $$ \begin{aligned} & x^2+2x-3 = mx +2\\[1em] & x^2+(2-m)x-5 = 0 \\[1em] \end{aligned} $$ となります。

ここで、上式の判別式を計算すると $${D = (2-m)^2 +20 > 0}$$ となり、曲線と直線は すべての\({\hspace{1pt}m\hspace{2pt}}\)に対して\({\hspace{1pt}2\hspace{1pt}}\)つの交点を持つことが分かります。

ここで、曲線 \({y=x^2+2x-3}\) と 直線 \({y=mx +2}\) に囲まれた面積\({\hspace{1pt}S\hspace{2pt}}\)を図示すると、以下のようになります。

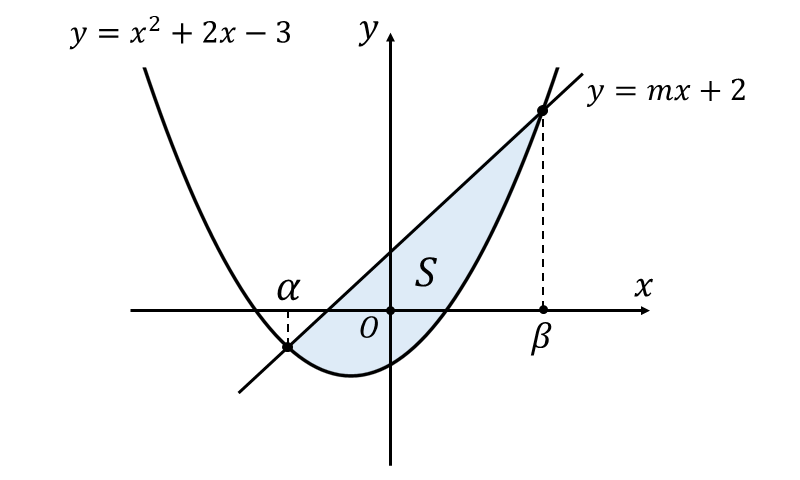
曲線 \({y=x^2+2x-3}\) と 直線 \({y=mx +2}\) の交点の \({x\hspace{1pt}}\)座標を \({x=\alpha,\hspace{2pt}\beta\hspace{3pt}}\) (\({\hspace{1pt}\alpha < \beta\hspace{2pt}}\)) とすると1/6公式から面積\({\hspace{1pt}S\hspace{2pt}}\)は以下のようになります。 $$ \begin{aligned} S=& \frac{|1|}{6}(\beta - \alpha)^3\\[1em] & = \frac{1}{6}(\beta - \alpha)^3 \\[1em] \end{aligned} $$

ここで \({\beta\hspace{1pt},\hspace{2pt}\alpha}\) は \({x^2+(2-m)x-5 = 0}\) の解であるため、解の公式から

よって、\({m=2}\) のとき \({\beta - \alpha}\) は最小値 \({2\sqrt{5}}\) となります。

したがって、このときの面積\({S\hspace{1pt}}\)が $$ \begin{aligned} S =& \frac{1}{6}(2\sqrt{5})^3\\[1em] & = \frac{20\sqrt{5}}{3} \\[1em] \end{aligned} $$ であることから、\({m=2}\) のとき 面積\({\hspace{1pt}S\hspace{2pt}}\)は最小値 \(\displaystyle{\frac{20\sqrt{5}}{3}}\) となります。

【関連するページ】
・定積分

・1/6公式