-光と光学に関連する用語の解説サイト-

正弦波の式

本項では以下の内容を解説しています。

・正弦波の式の意味
・正弦波の式の変形
・複素数表示

1. 正弦波の式
2. 正弦波の式の変形
3. 複素数表示

【1】正弦波の式とは

水面を伝わる波は、水面を上下に振動させながら、特定の方向に伝搬していきます。
また、音は空気の圧縮と膨張を繰り返しながら、特定の方向に伝搬します。

波とは、水や空気といった媒質の振動が、周囲の媒質に伝わっていく現象のことです。
波動光学の分野では、光を波として扱うことで、回折や干渉といった現象が説明されます。

本章では、波をどのように式で表現するかについて解説します。

【1-1】正弦波の式

最も基本的な波の式として、正弦波がよく使用されます。
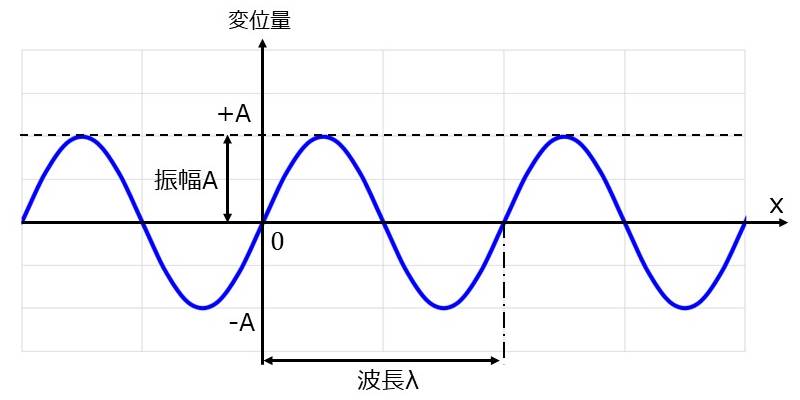
まず、図1のようにある時刻において、位置 $\large{x}$ が $\large{0}$ のとき変位が $\large{0}$ となるような正弦波について考えます。正弦波のイメージ

図1.ある時刻における正弦波の図

このとき、図1の正弦波は以下のように表せます。 $$\large{f(x)= A \sin \frac{2\pi}{\lambda}x \hspace{20pt}(1)}$$ 上式の $\large{A}$ は波の振れ幅を表し、$\large{x}$軸から波形の頂点までの距離、すなわち変位量の最大値を意味します。
また、$\large{\lambda}$ は波長を表し、波形の山と山の間隔を意味します。

また、$\displaystyle\large{\frac{2\pi}{\lambda}}$ の項は波数といいます。波数は記号 $\large{k}$ により記述されます。
波数$\displaystyle\large{k=\frac{2\pi}{\lambda}}$を使用することで、(1)式は以下のようにも表記されます。 $$\large{f(x)= A \sin kx}$$ 波数$\large{k}$ がなぜ $\displaystyle\large{\frac{2\pi}{\lambda}}$ と表されるのかは、別のページの『波数とは』に説明しています。

【1-2】時刻tの正弦波の式

正弦波が $\large{x}$軸方向に速度 $\large{v}$ で進行しているとき、時刻$\large{t}$ における波の式は、$\large{x}$軸方向に $\large{vt}$ だけ平行移動させることにより表現します。

以下の図2に、(1)式の正弦波と、その正弦波を $\large{vt}$ だけ平行移動させたときのグラフを示します。時刻tにおける正弦波のグラフ

図2.時刻tにおける正弦波の図

$\large{x}$軸の正方向に進行する正弦波は、(1)式の $\large{x}$ に $\large{x-vt}$ を代入することで、以下のように表せます。

【x軸の正方向に進行する正弦波】

$\large{ \displaystyle f(x,t)= A \sin \frac{2\pi}{\lambda}(x-vt)\hspace{20pt}(2)}$

一方、x軸の負方向に進行する正弦波は、(1)式の $\large{x}$ に $\large{x+vt}$ を代入し表現します。

【x軸の負方向に進行する正弦波】

$\large{ \displaystyle f(x,t)= A \sin \frac{2\pi}{\lambda}(x+vt)}$

【2】正弦波の式の変形

(2)式の時刻$\large{t}$ における正弦波の式は、パラメータを変形することで、様々な形式で記述されます。本章では、(2)式を変形して記述した正弦波の式について解説します。

・波長$\large{\lambda}$, 周期T による正弦波

波長 $\large{\lambda}$ 分だけ波が進行する時間を周期 $\large{T}$ といいます。
波が1周期分の進行する時間が周期 $\large{T}$ であることから、波の速度$\large{v}$、波長$\large{\lambda}$、周期$\large{T}$ の関係は以下のようになります。 $$ \large{v=\frac{\lambda}{T}\hspace{20pt}(3)}$$

(3)式を使用して、(2)式を変形すると以下のように表せます。

【波長$\large{\lambda}$, 周期T による正弦波】

$\large{ \displaystyle f(z,t)= A \sin \left(\frac{2\pi}{\lambda}z-\frac{2\pi}{T}t \right)}$

・波数$\large{k}$, 角周波数$\large{\omega}$ による正弦波

波数 $\displaystyle\large{k=\frac{2\pi}{\lambda}}$ と同様な形式で、角周波数 $\displaystyle\large{\omega=\frac{2\pi}{T}}$ というパラメータが使用されます。
波数$\large{k}$ と角周波数$\large{\omega}$ を使用すると、(2)式は以下のように表すことができます。

【波数$\large{k}$と角周波数$\large{\omega}$ による正弦波】

$\large{ \displaystyle f(z,t)= A \sin (kz-\omega t)}$

・速度$\large{v}$, 振動数$\large{f}$ による正弦波

単位時間に伝搬する波の数を振動数 $\large{f}$ といいます。
波が1周期分だけ伝達する時間を表す周期$\large{T}$ と振動数$\large{f}$ は、逆数の関係にあるため以下が成り立ちます。 $$\large{f= \frac{1}{T}}$$

ここで、(3)式より波の速度$\large{v}$ を振動数$\large{f}$ と波長$\large{\lambda}$ により表すと、以下のようになります。 $$\large{v=\frac{\lambda}{T} = \lambda f}$$

したがって、(2)式を振動数$\large{f}$ を使用して記述すると、以下のようになります。

【速度$\large{v}$, 振動数$\large{f}$ による正弦波】

$\large{ \displaystyle f(x,t)= A \sin 2\pi f \left(\frac{x}{v}-t \right)}$

・よく使われる正弦波の式の一覧

以上の内容をまとめると、x軸の正方向に進行する正弦波の式は、以下のような式で記述されます。 \begin{eqnarray} \large f(x,t)&=&\large A \sin \frac{2\pi}{\lambda}(x-vt)\\[0.7em] \large f(x,t)&=&\large A \sin \left(\frac{2\pi}{\lambda}z-\frac{2\pi}{T}t \right)\\[1em] \large f(x,t)&=&\large A \sin (kz-\omega t)\\[1em] \large f(x,t)&=&\large A \sin 2\pi f \left(\frac{x}{v}-t \right) \end{eqnarray}

また、x軸の負方向に進行する正弦波の式は、以下のように符号を変えて記述されます。 \begin{eqnarray} \large f(x,t)&=&\large A \sin \frac{2\pi}{\lambda}(x+vt)\\[0.7em] \large f(x,t)&=&\large A \sin \left(\frac{2\pi}{\lambda}z+\frac{2\pi}{T}t \right)\\[1em] \large f(x,t)&=&\large A \sin (kz+\omega t)\\[1em] \large f(x,t)&=&\large A \sin 2\pi f \left(\frac{x}{v}+t \right) \end{eqnarray}