光速 | 光速の値と測定方法
本項では、以下の内容について解説しています。
- ・光速が伝わる時間
- ・レーマーの光速測定
- ・フィゾーの光速測定
- ・フーコーの光速測定
【1】光速とは
光速(英:speed of light)とは、光(電磁波)が空間を伝搬する速さのことをいいます。
光は真空中において、\({\large{2.99792458 \times 10^{8}}}\)[m/s](秒速 約30万km)の速度で伝搬します(1)。
また、光速を時速に換算すると、\(\large{\rm{1.079252849} \times 10^{9}}\)[km/h](時速 約10億7900万km)の速度となります。
・光が伝わる時間
地球一周分の距離は約40075.017[km](2)です。 距離を光速で割ることにより地球一周分の距離を光が伝搬する時間を求めると、約0.13秒となります。
また、地球から月の平均距離は約384399[km]であり、地球一周の約10倍の距離です。地球と月がこれほど離れていても、光は約1秒で伝搬します。
| 距離[km] | 光が伝搬する時間 | |
|---|---|---|
| 地球一周 | 40075 | 0.13秒 |
| 地球-月 | 384399 | 1.28秒 |
また、地球と太陽の平均距離は約1億4960万km(\(\large{\rm{1.495978707\times 10^{11}}}\)[m])です(2)。
したがって、太陽の光が地球に伝わるまでの時間は、約8分19秒と計算されます。
つまり、地球上の人間が太陽の光を感じたとき、その光は8分19秒前に太陽から放たれているということになります。
以下の表に太陽から太陽系の惑星までの平均距離と、光が伝わるまでの時間をまとめています。
| 太陽からの距離 [\(\large{\times 10^8}\)km] |
光が伝搬する時間 | |
|---|---|---|
| 地球 | 1.496 | 8分19秒 |
| 火星 | 2.279 | 12分40秒 |
| 木星 | 7.783 | 43分16秒 |
| 土星 | 14.294 | 1時間19分28秒 |
| 天王星 | 28.750 | 2時間32分26秒 |
| 海王星 | 45.044 | 4時間10分25秒 |
【2】光速の測定
光速を直接測定するためには、光が離れた2点間を伝わるのに、どれほど時間がかかったかを測定する必要があります。
ガリレオ・ガリレイは、離れた位置にいる2人が提灯の明かりを付けたり、消したりを繰り返すことで、光速が有限であることを確かめようとしました。
しかし、先述したように、光は地球一周分の距離を0.13秒で進むほどの速さであり、地上の2点間ではあまりに距離が近すぎたため、光の速さを測定することはできませんでした。
人類で最初に光速の測定を成功させたのは、レーマーによる天文学からのアプローチでした。
レーマーは木星の衛星の食の周期を利用し、光が地球の公転の直径\(\large{2.8 \times 10^8 }\)kmを伝搬するのに、約22分かかることを示し、光速を求めました。
レーマーは地球の公転という天文学的な距離を測定に利用することで、光速の測定を可能にしました。
その後、フィゾーやフーコーらによって地上の装置により光速を測定する手法が研究されました。
先述したように、光は地球上では一瞬とも言える速度であるため、直接測定することが困難でした。そこで、地球上での測定は歯車や回転ミラーを使い、光を高速に点滅させるという手法が取られました。
光を歯車や回転ミラーで高速に点滅させ、地上の2点間を光が往復するのにかかる時間を測定することで、地上での測定を可能にしました。
次章以降で、上記の光速の測定方法について説明します。
【3】レーマーの光速の測定
レーマーは、木星の周囲を公転する衛星イオの食の観測時刻から光速を測定しています。
当時、衛星イオが木星の影に隠れる食の周期は、観察する月日によって変化することが知られていました。 レーマーは、この食の周期の変化は、光の速度が有限であるために発生していると考えました。
図1に、太陽の回りを公転する地球と、木星の周囲を公転する衛星イオの図を示します。

レーマーは地球と木星の距離が最も近い位置(位置A)と比較して、
最も遠い位置(位置B)において食の周期に22分の遅れが生じることを発見しました。
この遅れが地球の公転の直径分を光が進行するのにかかる時間と考え、光速を算出しました。
レーマーは、光速の大きさは\(\large{2.14 \times 10^8 [m/s] }\)という結果を得ました。この光速の値が、世界で初めて測定された光速であると言われています。(3)
【4】フィゾーの光速の測定
地上で初めて光速を測定した人物はフィゾーと言われています。
フィゾーは、回転する歯車を使用することで光速を実験的に求めることに成功しました。
図2にフィゾーが光速の測定で使用した実験系の概要を示します。
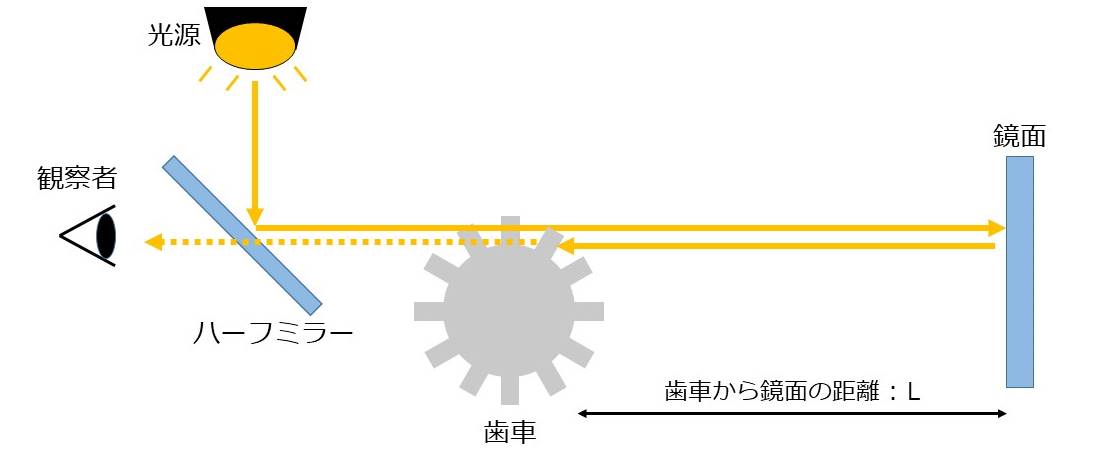
フィゾーの光速の測定では、まず光源から射出された光をハーフミラーで歯車に入射します。 (ハーフミラーとは、光を反射成分と透過成分に分ける光学素子です。)
歯車を通った光は遠方に設置された鏡面に反射され、再び歯車を通り観測者により観測されます。
鏡面から反射された光は、歯車の回転によって"歯に遮られる"もしくは"切り欠きを通る"ことで明るさが変化し、点滅を繰り返します。
このとき、歯車の切り欠きを通り鏡面で反射された光が、ちょうど歯に遮られるように歯車が回転しているとき、光が観測者に届かなくなります。
歯車が切り欠きから歯に切り替わる時間は、歯車から鏡面までを光が往復する時間に相当すると考えられます。 歯車から鏡面を往復する時間と距離を求めることができるため、光の速さを計算することができます。
・フィゾーの光速測定の計算方法
ここで、フィゾーの光速の測定における光速の計算方法について解説します。
図2の実験系において、歯車の歯の数が\(\large{n}\)[個]、歯車から鏡面までの距離を\(\large{l}\)[m]とします。
そして、歯車が静止した状態から回転数を速くしていったときに、ちょうど歯車の1秒あたりの回転数が\(\large{f}\)[回/秒]であるときに 初めて反射光が見えない状態になったとします。
先述したように、歯車の切り欠きを通った光が、ちょうど歯に遮られるときに反射光が見えない状態となります。
図3に切り欠きを通った光(図3左)が、歯に遮られる様子(図3右)を示します。

図3のように、歯車の歯の数が8個のとき、光が切り欠きを通り、次の歯に遮られるまでに、歯車は\(\large{\frac{1}{8} \times \frac{1}{2}=\frac{1}{16}}\)だけ
回転することになります。
よって、歯車の歯の数が\(\large{n}\)個であるとき、歯車が\(\large{\frac{1}{2n}}\)だけ回転することで、反射光が見えない状態となります。
歯車の1秒あたりの回転数が\(\large{f}\)[回/秒]であるとき、1回転にかかる時間は\(\large{\frac{1}{f}}\)[秒/回]となります。
したがって、歯車が\(\large{\frac{1}{2n}}\)だけ回転する時間\(\large{T}\)[秒]は、 $$\large{T=\frac{1}{f} \times \frac{1}{2n} = \frac{1}{2nf}}$$ となります。
以上より、歯車と鏡面までの距離が\(\large{l}\)のとき、光速c[m/s]は以下のように求められます。 $$\large{c=\frac{2l}{T}=2l \times 2nf = 4nfl}$$
フィゾーの測定結果によると、\(\large{720}\)の歯を持つ歯車を使用し、歯車と鏡面の間隔が\(\large{8633}\)[m]であるとき、回転数が\(\large{12.6}\)[回/秒]のとき 初めて反射光が見えない状態となりました。(3) 測定値を代入すると、以下のように計算できます。 $$\large{c= 4nfl = 4 \times 720 \times 12.6 \times 8633}$$ したがって、光速cの値は以下のようになります。 $$\large{c = 313,274,304[m/s]}$$
【5】フーコーの光速の測定
フーコー(Foucault)は1850年に、高速回転する鏡を使用して光速の測定に成功しています。
図4に、フーコーによる光速の測定の概略図を示します。黄色線で鏡\(\large{M_2}\)に入射するまでの光、赤線で鏡\(\large{M_2}\)で反射後の光の経路を示します。

光源から照射された光は、高速回転する鏡\(\large{M_1}\)により反射されます。
鏡\(\large{M_1}\)によって反射された光は、鏡\(\large{M_1}\)の回転によって進行する方向が変化し、そのうち遠方の固定された鏡\(\large{M_2}\)に到達した光のみが、図3の赤線で示された光源に戻る光となります。
鏡\(\large{M_1}\)で反射し、鏡\(\large{M_2}\)に到達した後、再び鏡\(\large{M_1}\)に戻るまでの時間に、鏡\(\large{M_1}\)は回転し角度を変化させます。
鏡\(\large{M_1}\)の角度が変化することで、鏡\(\large{M_1}\)に入射した光の経路とは異なる角度で光が光源に戻ってきます。
光源の前にハーフミラーを置くことで、光源に戻ってきた光の位置がどれだけ変化したかを観察します。
光が鏡\(\large{M_1,M_2}\)を往復する時間に応じて、像の位置が変化することから光速を割り出すことができます。
フィゾーの歯車を利用した測定では、測定結果が光の明るさとして観察されます。フィゾーの測定では、光の明るさの変化を人の目で読み取るため、測定の精度には限界がありました。
一方、フーコーの回転する鏡を使用した測定では、測定結果が光の位置の変化量として観察されるため、より精度の高い測定が可能となりました。
フーコーはこの回転鏡による実験により、光の速度が\(\large{c = 298,000,000 \pm 500,000}\)[m/s]という結果を得ました。(3)
・フーコーによる測定の光速の計算式
フーコーの測定により光速を計算する式を導出します。
図5のように、鏡\(\large{M_1,M_2}\)間の距離を\(\large{L}\)、光源から回転する鏡\(\large{M_1}\)までの距離を\(\large{R}\)、光源に戻る光の位置の変化量を\(\large{d}\)とします。

鏡\(\large{M_1}\)が1秒間に\(\large{f}\)[回]だけ回転すると、1回転分の角度は\(\large{2 \pi}\)[rad]のため、鏡\(\large{M_1}\)は1秒間に\(\large{2 \pi f}\)[rad]の角度だけ回転します。
したがって、光が往復するt秒間に鏡\(\large{M_1}\)の角度が\(\large{\alpha}\)[rad]だけ変化したとすると、以下の式が成り立ちます。 $$\large{\alpha = 2 \pi f t}$$
また、鏡\(\large{M_1}\)が角度\(\large{\alpha}\)だけ回転すると、反射光線の角度\(\large{\theta}\)は\(\large{2\alpha}\)だけ変化するため、\(\large{\theta = 2 \alpha}\)が成り立ちます。(回転する鏡の反射についてはこちらで解説しています。)
したがって、上式から鏡\(\large{M_1}\)の角度\(\large{\alpha}\)を削除し、光源に戻る光線の角度\(\large{\theta}\)で表現すると、以下のようになります。
ここで、回転する鏡\(\large{M_1}\)と鏡\(\large{M_2}\)を往復する時間\(\large{t}\)は、光速を\(\large{c}\)、\(\large{M_1,M_2}\)間の距離を\(\large{L}\)とすると、以下のように求められます。 $$\large{t = \frac{2L}{c} \hspace{10pt}(3)}$$
(2)式と(3)式から時間tを削除すると、以下の式になります。 $$\large{\theta = 4 \pi f \frac{2L}{c}}$$ 上式から、鏡\(\large{M_1,M_2}\)間の距離\(\large{L}\)、ミラー\(\large{M_1}\)の単位時間あたりの回転数\(\large{f}\)、光源に戻る光の角度\(\large{\theta}\)から光速\(\large{c}\)を計算する式を導くことができます。
\(\large{\displaystyle c = \frac{8 \pi f L}{\theta}\hspace{10pt}(4)}\)
ここで、(4)式を光源に戻る光の位置のズレ量\(\large{d}\)から、光速\(\large{c}\)を計算する式に変形します。
図5から、回転鏡\(\large{M_1}\)から光源までの距離が\(\large{R}\)、像のズレ量が\(\large{d}\)であるとき、光源に戻る光の角度\(\large{\theta}\)とは以下の関係があります。
$$\large{d=R \theta} $$
上式から、測定される像のズレ量\(\large{d}\)、装置の各部の長さ\(\large{L,R}\)、ミラー\(\large{M_1}\)の単位時間あたりの回転数\(\large{f}\)から光速を算出することができます。
\(\large{\displaystyle c= \frac{8 \pi f L R}{d}\hspace{10pt}(4')}\)
参考文献
・(1)国立天文台『理科年表 平成27年』丸善出版株式会社,平成26年11月30日発行, pp374
・(2)国立天文台『理科年表 平成27年』丸善出版株式会社,平成26年11月30日発行, pp77-79
地球1周の距離は、p77の赤道半径6378.137[km]から計算した
太陽から惑星の距離は、p78-79の表中の太陽からの距離 長半径aの欄から引用した
・(3)霜田光一『パリティブックス 歴史をかえた物理実験』丸善出版株式会社,平成29年10月30日発行,5章 光の速さ pp65-73