薄膜の干渉とは

本項では以下の内容を解説しています。

• ・薄膜による反射光の干渉
• ・薄膜による透過光の干渉
• ・計算問題

薄膜での干渉は、物質の境界面で入射光が反射光と透過光に分離され、2つの経路に分かれた光が干渉することで発生します。

シャボン玉が色付いて見えたり、水面の油膜が虹色に見えたりする現象は、この薄膜による光の干渉により説明することができます。

本項で解説する2つの経路に分割された光の干渉を、二光束干渉といいます。一方、多くの光に分割された光の干渉を多光束干渉といいます。多光束干渉については別のページで解説しています。

本項では、薄膜で発生する干渉縞の発生条件や、計算例について解説します。

【1】薄膜での反射光の干渉

本章では、薄膜に平面波が入射したときの反射光による干渉縞の条件を求めます。

図1のように屈折率\(\large{n_1}\)の媒質中に、屈折率\(\large{n_2}\)、厚み\(\large{d}\)の薄い膜がある場合を考えます。
この膜に入射角\(\large{\theta_1}\)で平面光が入射し、その反射光による干渉縞を観察するとします。

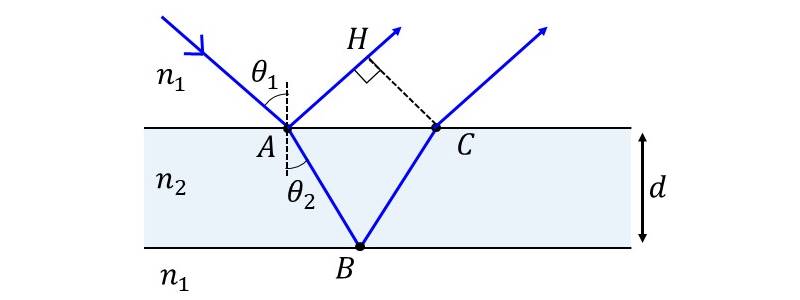
【1-1】光路差の計算

薄膜に入射した光は、点Aにおいて反射光と透過光に分かれます。

また、点Aで透過した光は、点Bで反射された後、点Cにおいて元の媒質に透過します。 (点Cで反射する成分は反射率が小さいとして無視します。)

ここで、点Aで反射される光と、点Bで反射される光の干渉について考えます。 2経路の光路差は以下の式により表されます。(\(\large{\overline{AB}}\)などは、点Aと点B間の距離を表します。\(\large{\overline{AB}}\)に物質の絶対屈折率\(\large{n}\)をかけた値が光路長を意味します。)

$$\large{n_2(\overline{AB} + \overline{BC}) - n_1 \overline{AH}}$$

\(\large{\overline{AB}}\)は、\(\large{\cos{\theta_2}=\frac{d}{\overline{AB}}}\)であることから、 $$\large{\overline{AB}=\frac{d}{\cos{\theta_2}}}$$

\(\large{\overline{BC}}\)も同様にして、 $$\large{\overline{BC}=\frac{d}{\cos{\theta_2}}}$$

また、図1より、\(\large{\overline{AC}=2 d \tan{\theta_2}}\)であることから、 $$\large{\overline{AH}=2d \tan{\theta_2} \sin{\theta_1}}$$

以上より、光路差は以下のようになります。 $$\large{n_2(\overline{AB} + \overline{BC}) - n_1 \overline{AH} = \frac{2 n_2d}{\cos{\theta_2}} - 2 n_1 d \tan{\theta_2} \sin{\theta_1}}$$ ここで、\(\large{n_1 \sin{\theta_1}=n_2 \sin{\theta_2}}\)より \begin{eqnarray} \large \frac{2 n_2d}{\cos{\theta_2}} - 2 n_1 d \tan{\theta_2} \sin{\theta_1}&\large =&\large \frac{2 n_2d}{\cos{\theta_2}}-2 n_2 d \tan{\theta_2} \sin{\theta_2}\\ &\large =&\large \frac{2 n_2d}{\cos{\theta_2}}(1- \sin^2{\theta_2})\\ &\large =&\large 2 n_2d\cos{\theta_2}\\ \end{eqnarray} したがって、 $$\large{n_2(\overline{AB} + \overline{BC}) - n_1 \overline{AH} = 2 n_2d\cos{\theta_2}}$$

【1-2】干渉の明暗の条件の導出

ここで、点Aと点Bで発生する反射は、媒質の屈折率\(\large{n_1}\)と膜の屈折率\(\large{n_2}\)の大小関係によって位相が変化します。

\(\large{n_1 > n_2}\)であるときは、点Bで屈折率の大きい物質から小さい物質への反射となり、位相が\(\large{\pi}\)だけ変化します。 一方、\(\large{n_2 > n_1}\)であるときは、点Aにおいて位相が\(\large{\pi}\)だけ変化することになります。

上記のどちらの場合においても、位相は\(\large{\pi}\)だけ変化することになり、明暗の縞の条件式も１つにまとめることができます。

スネルの法則から屈折角\(\large{\theta_2}\)を削除すると、以下のように入射角\(\large{\theta_1}\)の条件としても表現できます。

【2】薄膜での透過光の干渉

本章では、図2のような薄膜を透過した光の干渉の縞の条件について考えます。

【2-1】光路長差の計算

透過光について干渉を考える場合は、点Bにおいて反射光と透過光で分かれるため、点Bを基準として光路長差を計算します。

図2より、2経路の光路長差は以下により表されます。 $$\large{n_2(\overline{BC} + \overline{CD}) - n_1 \overline{BK}}$$

反射による干渉と同様の計算により、上記の光路長は以下により表されます。 $$\large{\overline{BC} = \overline{CD} = \frac{d}{\cos{\theta_2}}}$$ $$\large{\overline{BK} = 2d \tan{\theta_2} \sin{\theta_1}}$$

よって、光路長差は以下のようになります。 \begin{eqnarray} \large n_2(\overline{BC} + \overline{CD}) - n_1 \overline{BK}&\large =&\large 2 n_2 \frac{d}{\cos{\theta_2}} - 2 n_1 d \tan{\theta_2} \sin{\theta_1}\\ &\large =&\large 2 n_2 d \cos{\theta_2}\\ \end{eqnarray}

【2-2】透過による干渉の明暗の条件

ここで、BCDを経由した光は、合計で2回反射されることになります。そのため、反射によって位相が変化した場合も、2回の反射により相殺されるため、 境界面の反射による位相の変化は考える必要がありません。

以上より、透過光による干渉縞の条件は以下のようになります。

反射光の場合と同様に、スネルの法則から屈折角\(\large{\theta_2}\)を削除すると、入射角\(\large{\theta_1}\)の条件としても表現できます。

【3】薄膜の干渉の計算問題

本章では、薄膜の干渉に関連した計算問題を解説します。

【3-1】薄膜の干渉の計算

【回答と解説】
以下の入射光\(\large{\theta_1}\)に依存した反射光による干渉で明るい縞のできる条件を利用して波長を求めます。 $$\large{\displaystyle 2 d \sqrt{{n_2}^2-{n_1}^2 {(\sin{\theta_1})}^2} = \frac{1}{2}(2m +1) \lambda_0}$$ 上記の条件を波長について整理すると以下のようになります。 $$\large{\displaystyle \lambda_0 = \frac{4d}{2m+1} \sqrt{{n_2}^2-{n_1}^2 {(\sin{\theta_1})}^2}}$$ 上式のmを適当に変化させ、可視光域380～780nmに適合する波長を見つけることで、明るい縞の観測される波長を求めます。

求める波長は、m=2のとき721nm, m=3のとき515nm,m=4のとき400nmとなります。

シャボン玉や水面の油膜が色付いて見える現象は、入射した太陽光の可視光のうち、特定の色の波長のみが干渉により明るく見えるためと考えることができます。

---