放物線と2つの接線に囲まれた面積
◆第問目!
\({C}\) 上の点\({(\hspace{1pt}-1\hspace{1pt},\hspace{1pt}11\hspace{1pt})}\) , \({(\hspace{1pt}2\hspace{1pt},\hspace{1pt}5\hspace{1pt})}\) における接線 と \({C}\) によって囲まれる面積\({S\hspace{2pt}}\)を求めよ
まず、放物線上の接線の方程式を求めます。
次にグラフを描いて関数の上下関係を調べてから積分します。
放物線 \({y=ax^2+bx+c}\) と 2本の接線との接点を \({x=\alpha,\hspace{2pt}\beta}\) としたとき囲まれる面積\({\hspace{1pt}S\hspace{2pt}}\)を求める1/12公式
$$\displaystyle{S = \frac{|a|}{12}(\beta-\alpha)^3}$$
を用いると簡単に計算ができます。
【解答のポイント】
まず、放物線上の接線の方程式を求めます。
次にグラフを描いて関数の上下関係を調べてから積分します。
放物線 \({y=ax^2+bx+c}\) と 2本の接線との接点を \({x=\alpha,\hspace{2pt}\beta\hspace{3pt}}\) とすると囲まれる面積\({\hspace{1pt}S\hspace{2pt}}\)を求める1/12公式
$$\displaystyle{S = \frac{|a|}{12}(\beta-\alpha)^3}$$
を用いると簡単に計算ができます。(別解に記載)
【解答】
\({f(x)=2x^2-4x+5}\) とすると \({f'(x)=4x-4}\) となります。
つまり、点\((-1,11)\) における接線の傾きは \({f'(-1)=-8}\) となります。
したがって、接線の方程式の公式 $${y=f'(a)(x-a)+f(a)}$$ から、求める接線の方程式は
と求められます。
また、点\((2,5)\) における接線の傾きは \({f'(2)=4}\) となります。
したがって、求める接線の方程式は
と求められます。
2つの接線の方程式から、交点の\({\hspace{1pt}x\hspace{2pt}}\)座標を求めると $$ \begin{aligned} -8x+3 & = 4x-3 \\[0.5em] x & = \frac{1}{2} \\[0.5em] \end{aligned} $$ となります。
放物線 \({y=2x^2-4x+5}\) と 2つの接線 \({y=-8x+3}\) と \({y=4x-3}\) に囲まれた面積を図示すると、以下のようになります。
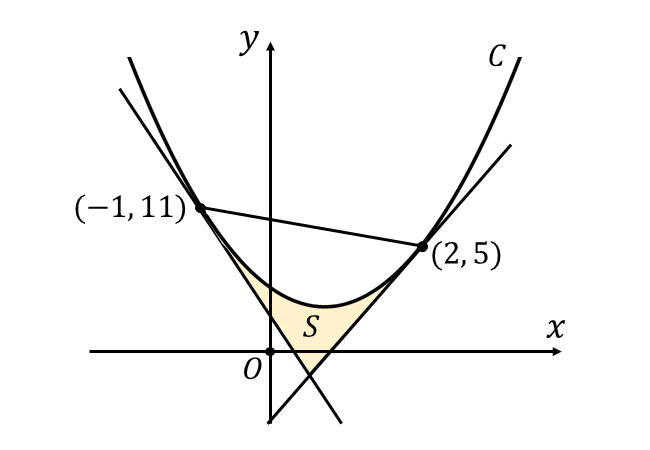
上図から、\({-1 \leqq x \leqq 2}\) において放物線 \({y=2x^2-4x+5}\) は2つの接線の上側にあるので、面積\({\hspace{1pt}S\hspace{2pt}}\)は以下のように求められます。
【別解】
放物線 \({y=ax^2+bx+c}\) と 2本の接線との接点 \({x=\alpha,\hspace{2pt}\beta\hspace{3pt}}\) に囲まれる面積\({\hspace{1pt}S\hspace{2pt}}\)を求める1/12公式
$$\displaystyle{S = \frac{|a|}{12}(\beta-\alpha)^3}$$
において、放物線の二次の係数が \({a=2}\)、接点の\({x\hspace{1pt}}\)座標が \({\alpha=-1,\hspace{2pt}\beta=2}\) であることから面積は
$$
\begin{aligned}
\hspace{10pt} S & = \frac{|2|}{12}(2-(-1))^3\\[0.5em]
& = \frac{9}{2} \\[0.5em]
\end{aligned}
$$
と求められます。
【関連するページ】
・定積分