絶対値のついた三角関数の定積分
◆第問目!
$${\int_0^\pi |3 \sin x + \cos x| \hspace{1pt}dx}$$
絶対値を含む定積分は、まず絶対値の記号を外す必要があります。
問題の被積分関数は三角関数の和であるため、三角関数の合成をしてから絶対値の記号を外します。
三角関数の合成から $${3 \sin x + \cos x = \sqrt{10}\sin(x + \alpha)}$$ と変形できますが、\({\alpha\hspace{2pt}}\)を具体的に求めることができませんが、そのまま積分を計算します。
【解答のポイント】
絶対値を含む定積分は、まず絶対値の記号を外す必要があります。
問題の被積分関数は三角関数の和であるため、三角関数の合成をしてから絶対値の記号を外します。
三角関数の合成から $${3 \sin x + \cos x = \sqrt{10}\sin(x + \alpha)}$$ と変形できますが、\({\alpha\hspace{2pt}}\)を具体的に求めることができませんが、そのまま積分を計算します。
【解答】
三角関数の合成の公式から $${a \sin x + b \cos x = r \sin (x + \alpha)}$$ に対して \({r=\sqrt{a^2+b^2}\hspace{1pt},\hspace{2pt}}\)\(\displaystyle{\sin \alpha = \frac{b}{r}\hspace{1pt},\hspace{2pt}}\)\( \displaystyle{\cos \alpha = \frac{a}{r}}\) を計算します。
\({r=\sqrt{3^2 + 1^2} = \sqrt{10}}\) から $${3 \sin x + \cos x = \sqrt{10}\sin(x + \alpha)}$$ と変形されます。
ここで \({\alpha}\) は \(\displaystyle{ \sin \alpha = \frac{1}{\sqrt{10}}\hspace{1pt},\hspace{2pt}}\)\( \displaystyle{\cos \alpha = \frac{3}{\sqrt{10}}}\) であり、\({0 < \alpha < \frac{\pi}{2} }\) を満たします。
\({y=\sqrt{10}\sin(x + \alpha)\hspace{2pt}}\)のグラフを描くと以下のようになります。
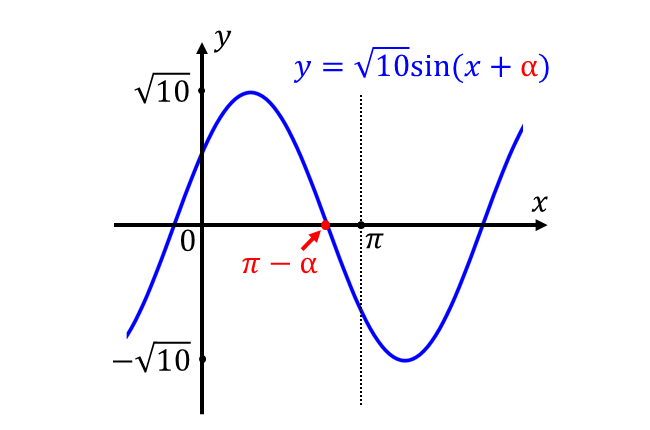
すなわち、絶対値を外して積分すると以下のようになります。
上記の計算の過程で三角関数の性質から $${\cos(\pi+\alpha) = - \cos \alpha}$$ と変形しています。
【関連するページ】
・三角関数の合成