-光と光学に関連する用語の解説サイト-

減衰曲線e^(-x)sinxの面積

◆第問目！

【 難易度 ★★★★★ 】
　曲線\({\hspace{1pt}y=e^{-x}\sin x\hspace{2pt}}\) \({(\hspace{1pt}x \geqq 0\hspace{1pt})}\) と \({\hspace{1pt}x\hspace{2pt}}\)軸 に囲まれた面積を求めよ

\({y=e^{-x}\sin x\hspace{2pt}}\)と\({\hspace{1pt}x\hspace{2pt}}\)軸との交点は、\({x \geqq 0\hspace{1pt}}\)において\({\hspace{1pt}\sin x = 0\hspace{2pt}}\)となる点であるため、\({x=k \pi\hspace{2pt}}\)(\({\hspace{1pt}k\hspace{2pt}}\)は\({\hspace{1pt}0\hspace{2pt}}\)以上の整数)となります。

区間 \({[\hspace{1pt}k \pi \hspace{1pt},\hspace{1pt} (k+1)\pi\hspace{1pt}]}\) における面積は以下のように表されます。 $${\int_{ k \pi}^{ (k+1) \pi} |e^{-x} \sin x|\hspace{1pt}dx}$$

問題の面積は上記の積分を\({\hspace{2pt}x \geqq 0\hspace{1pt}}\)の範囲で足し合わせたものとなります。

【解答のポイント】

曲線\({\hspace{1pt}y=e^{-x}\sin x\hspace{2pt}}\) は減衰曲線といい、以下のように\({\hspace{1pt}x\hspace{2pt}}\)軸を中心に振動し、\({x\hspace{2pt}}\)が大きいほどその振動の振れ幅が小さくなるグラフとなります。
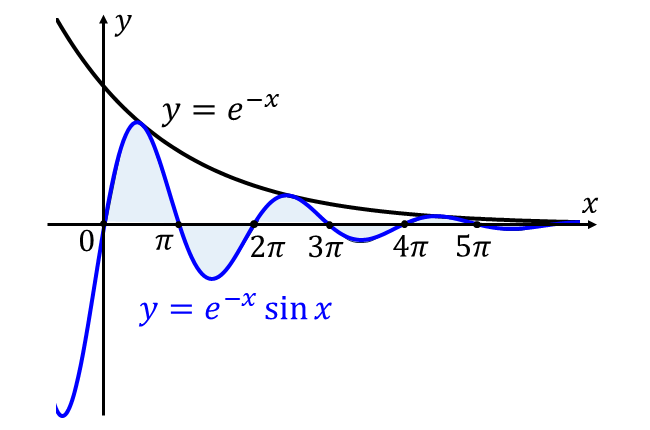
(以下のグラフは振動の様子が見やすいように加工しているため厳密ではありません) 減衰曲線e^(-x)sinxに囲まれた面積を求める問題

曲線\({\hspace{1pt}y=e^{-x}\sin x\hspace{2pt}}\) \({(\hspace{1pt}x \geqq 0\hspace{1pt})}\) と \({\hspace{1pt}x\hspace{2pt}}\)軸 に囲まれた面積とは、上図の青で塗られた領域を足し合わせた面積となります。

【解答】

\({y=e^{-x}\sin x\hspace{2pt}}\)と\({\hspace{1pt}x\hspace{2pt}}\)軸との交点は、\({x \geqq 0\hspace{1pt}}\)において\({\hspace{1pt}\sin x = 0\hspace{2pt}}\)となる点であるため、\({x=k \pi\hspace{2pt}}\)(\({\hspace{1pt}k\hspace{2pt}}\)は\({\hspace{1pt}0\hspace{2pt}}\)以上の整数)となります。

区間 \({[\hspace{1pt}k \pi \hspace{1pt},\hspace{1pt} (k+1)\pi\hspace{1pt}]}\) における面積は以下のように表されます。 $${\int_{ k \pi}^{ (k+1) \pi} |e^{-x} \sin x|\hspace{1pt}dx}$$

問題の求める面積は、\({\hspace{1pt}x \geqq 0\hspace{2pt}}\)の範囲で足し合わせたものとなるため、以下のような定積分で表されます。 $${\lim_{n \to \infty} \sum_{k=0}^{n-1}\int_{ k \pi}^{ (k+1) \pi} |e^{-x} \sin x|\hspace{1pt}dx}$$

\({k \pi \leqq x \leqq (k+1)\pi \hspace{2pt}}\)において被積分関数の符号が一定なので

$${\hspace{10pt}\int_{ k \pi}^{ (k+1) \pi} |e^{-x} \sin x|\hspace{1pt}dx = \left|\int_{k \pi}^{(k+1) \pi} e^{-x} \sin x\hspace{1pt}dx \right|\hspace{10pt}}$$

となります。

ここで \(\displaystyle{I=\int e^{-x} \sin x\hspace{1pt}dx}\) を求めます。

部分積分から

$$ \begin{aligned} \hspace{10pt}I & = \int e^{-x} \sin x \hspace{1pt}dx \\[1em] &= \int (-e^{-x})' \sin x \hspace{1pt}dx \\[1em] &= -e^{-x} \sin x - \int (-e^{-x}) \cos x \hspace{1pt}dx\\[1em] &= -e^{-x} \sin x + \int e^{-x} \cos x \hspace{1pt}dx\\[1em] \end{aligned} $$

ここで、\({ \int e^{-x} \cos x \hspace{1pt}dx\hspace{1pt}\hspace{2pt}}\)を部分積分から計算すると

$$ \begin{aligned} \hspace{10pt}& \int e^{-x} \cos x \hspace{1pt}dx \\[1em] &= \int (-e^{-x})' \cos x \hspace{1pt}dx \\[1em] &= -e^{-x} \cos x - \int (-e^{-x}) (-\sin x) \hspace{1pt}dx\\[1em] &= -e^{-x} \cos x - \int e^{-x} \sin x \hspace{1pt}dx\\[1em] &= -e^{-x} \cos x - I\\[1em] \end{aligned} $$

となります。

したがって $${I = -e^{-x} \sin x -e^{-x} \cos x - I}$$ となることから $${I = -\frac{1}{2}e^{-x}(\sin x + \cos x)+C}$$ と求められます。

よって \(\displaystyle{\left|\int_{ k \pi}^{(k+1) \pi} e^{-x} \sin x\hspace{1pt}dx \right|}\) を求めると

$$ \begin{aligned} \hspace{15pt}& \left|\int_{ k \pi}^{ (k+1) \pi} e^{-x} \sin x\hspace{1pt}dx \right|\\[1em] &= \left| \left[ -\frac{1}{2}e^{-x}(\sin x + \cos x) \right]_{k \pi}^{(k+1) \pi} \right|\hspace{10pt} \\[1em] &= \left| -\frac{1}{2} \left(e^{-(k+1)\pi}\left(\sin (k+1)\pi + \cos (k+1)\pi \right) - e^{-k\pi}\left(\sin k\pi + \cos k\pi \right)\right)\right|\hspace{10pt} \\[1em] &= \left| -\frac{1}{2} \left(e^{-(k+1)\pi}(-1)^{k+1} - e^{-k\pi}(-1)^{k}\right)\right| \\[1em] &=\frac{1}{2} \left(e^{-(k+1)\pi} + e^{-k\pi}\right)\\[1em] &=\frac{1}{2} e^{-(k+1)\pi} \left(1 + e^{\pi}\right)\\[1em] \end{aligned} $$

(上記の計算では \({\sin k \pi=0\hspace{2pt},\hspace{2pt}\cos k \pi=(-1)^k}\) から式変形しています。)

したがって、求める面積は

$$ \begin{aligned} \hspace{10pt}& \lim_{n \to \infty} \sum_{k=0}^{n-1}\int_{\pi k}^{\pi (k+1)} |e^{-x} \sin x|\hspace{1pt}dx\\[1em] &= \lim_{n \to \infty} \sum_{k=0}^{n-1}\left|\int_{\pi k}^{\pi (k+1)} e^{-x} \sin x\hspace{1pt}dx \right| \\[1em] &= \lim_{n \to \infty} \sum_{k=0}^{n-1}\frac{1}{2} e^{-(k+1)\pi} \left(1 + e^{\pi}\right)\\[1em] &= \frac{1}{2} \left(1 + e^{\pi}\right) \lim_{n \to \infty} \sum_{k=0}^{n-1} e^{-(k+1)\pi}\\[1em] \end{aligned} $$

\(\displaystyle{\hspace{1pt}\sum_{k=0}^{n-1} e^{-(k+1)\pi}\hspace{2pt}}\)は初項\({\hspace{1pt}e^{-\pi}\hspace{2pt}}\)、公比\({\hspace{1pt}e^{-\pi}\hspace{2pt}}\)の等比数列の和であるため $${\sum_{k=0}^{n-1} e^{-(k+1)\pi} = \frac{e^{-\pi}(1-e^{-\pi n})}{1-e^{-\pi}}}$$ となります。

すなわち

$$ \begin{aligned} \hspace{10pt}& \frac{1}{2} \left(1 + e^{\pi}\right) \lim_{n \to \infty} \sum_{k=0}^{n-1} e^{-(k+1)\pi}\\[1em] &= \frac{1}{2} \left(1 + e^{\pi}\right) \lim_{n \to \infty} \frac{e^{-\pi}(1-e^{-\pi n})}{1-e^{-\pi}} \\[1em] \end{aligned} $$

ここで、\(\displaystyle{\hspace{1pt}e^{-\pi n} = \left( \frac{1}{e^{\pi}}\right)^n}\)であり、\(\displaystyle{0 < \frac{1}{e^{\pi}} < 1\hspace{2pt}}\)であることから、\(\displaystyle{\lim_{n \to \infty} e^{-\pi n} =0\hspace{2pt}}\)となります。

したがって

$$ \begin{aligned} & = \frac{1}{2} \left(1 + e^{\pi}\right) \lim_{n \to \infty} \frac{e^{-\pi}(1-e^{-\pi n})}{1-e^{-\pi}}\\[1em] &= \frac{1}{2} \left(1 + e^{\pi}\right) \frac{e^{-\pi}}{1-e^{-\pi}} \\[1em] &= \frac{1}{2} \left(1 + e^{\pi}\right) \frac{1}{e^{\pi}-1} \\[1em] &= \frac{e^{\pi}+1}{2(e^{\pi}-1)} \\[1em] \end{aligned} $$

【関連するページ】
・定積分

　【出題範囲】　　　【難易度】


　



Copyright (c) 光学技術の基礎用語 All Rights Reserved.