-光と光学に関連する用語の解説サイト-

円環体の体積を積分から求める問題

◆第問目！

【 難易度 ★★ 】
　\(\displaystyle{(x-a)^2+y^2=r^2\hspace{2pt}}\)\({(\hspace{1pt}0 < r < a\hspace{2pt}\hspace{1pt})}\) に囲まれた部分を\({\hspace{1pt}y}\)軸の周りに回転させた回転体の体積を求めよ

本問は回転軸から離れた位置の円を回転させたときの回転体の体積を求めるため、円環体(ドーナツの形状)の体積を求めることになります。

本問は\({\hspace{1pt}y}\)軸の周りに回転させるという点に注意が必要です。

\({\hspace{1pt}y}\)軸の周りに回転させる場合は \({\hspace{1pt}x=f(y)\hspace{2pt},\hspace{1pt}x=g(y)\hspace{2pt}}\)が区間\({\hspace{1pt}[a,b]\hspace{2pt}}\)において\({\hspace{1pt}f(y) \geqq g(y) \geqq 0 \hspace{2pt}}\)であるとき、

$$\hspace{10pt}{V= \pi \int_a^b (f(y))^2 \hspace{1pt}dy - \pi \int_a^b (g(y))^2 \hspace{1pt}dy}\hspace{10pt}$$

と求められます。

【解答のポイント】

本問は\({\hspace{1pt}y}\)軸の周りに回転させるという点に注意が必要です。

\({\hspace{1pt}y}\)軸の周りに回転させる場合は \({\hspace{1pt}x=f(y)\hspace{2pt},\hspace{1pt}x=g(y)\hspace{2pt}}\)が区間\({\hspace{1pt}[a,b]\hspace{2pt}}\)において\({\hspace{1pt}f(y) \geqq g(y) \geqq 0 \hspace{2pt}}\)であるとき、

$$\hspace{10pt}{V= \pi \int_a^b (f(y))^2 \hspace{1pt}dy - \pi \int_a^b (g(y))^2 \hspace{1pt}dy}\hspace{10pt}$$

と求められます。

【解答】

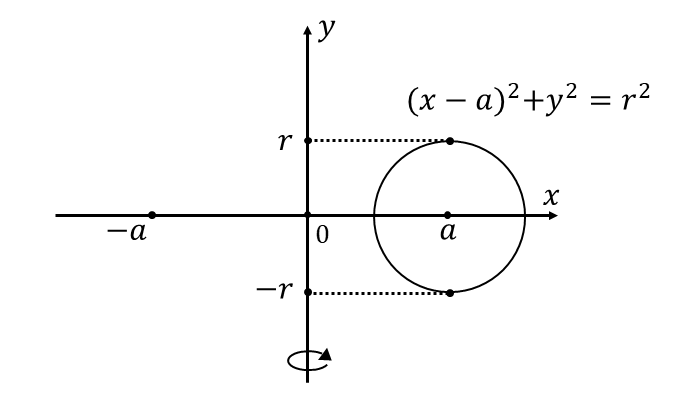
問題の円を図に描くと以下のようになります。 円環体の体積を積分により求める問題

問題の円の方程式\({\hspace{1pt}(x-a)^2+y^2=r^2\hspace{2pt}}\)を\({\hspace{1pt}x=\cdots\hspace{2pt}}\)の式に変形すると $$ \begin{aligned} \hspace{10pt}(x-a)^2 &= r^2 - y^2 \\[1em] x-a &= \pm \sqrt{r^2 - y^2} \\[1em] x &= a \pm \sqrt{r^2 - y^2} \\[1em] \end{aligned} $$ となります。

したがって、上図の円を\({\hspace{1pt}y}\)軸の周りに回転させた回転体の体積は以下のように求められます。

$$ \begin{aligned} \hspace{10pt}& \pi \left( \int_{-r}^{r} \left( (a + \sqrt{r^2 - y^2} )^2 - (a-\sqrt{r^2 - y^2} )^2 \right)\hspace{1pt}dx \right) \\[1em] & = 8\pi a \int_{0}^{r} \sqrt{r^2 - y^2} \hspace{1pt}dx \\[1em] & = 8\pi a \cdot \frac{1}{4} \pi r^2 \\[1em] & = 2\pi^2 r^2 a \\[1em] \end{aligned} $$

と求められます。

(上記の計算過程には\(\displaystyle{\hspace{1pt}\int_{0}^{r} \sqrt{r^2 - y^2} \hspace{2pt}}\)は半径\({\hspace{1pt}r\hspace{2pt}}\)の円の面積の4分の1を表すことから $${\int_{0}^{r} \sqrt{r^2 - y^2} = \frac{1}{4}\pi r^2}$$ であることを使用しています。)

【関連するページ】
・円の面積を求める積分

　【出題範囲】　　　【難易度】


　



Copyright (c) 光学技術の基礎用語 All Rights Reserved.